wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 22 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 161 975 volte
La deviazione standard ti permette di comprendere la distribuzione dei dati presenti nel campione. Per trovare questo valore dal tuo campione o dal tuo insieme di dati, devi eseguire alcuni calcoli. Prima di tutto devi trovare la media e la varianza dei dati; la varianza è la misura di quanto i dati si discostano dalla media. La deviazione standard si ricava estraendo la radice quadrata della varianza. Questo articolo ti mostrerà come procedere.
Passaggi
Trovare la Media
-
1Esamina i dati. Questo è un passaggio importante nel calcolo statistico anche per trovare un valore semplice come la media o la mediana.
- Sappi quanti numeri ci sono nel campione.
- I valori sono molto diversi fra loro o differiscono solo per pochi decimali?
- Sappi a cosa si riferiscono i dati che stai osservando. Che cosa rappresentano? Potrebbero essere i risultati di un esame, i rilevamenti del battito cardiaco, dei pesi, altezze e così via.
- Ad esempio, una serie di voti di un esame potrebbe essere: 10, 8, 10, 8, 8 e 4.
-
2Riunisci tutti i dati. Per calcolare la media devi avere tutti i valori presenti nel campione in oggetto.
- La media è appunto il valore medio dei numeri del tuo insieme.
- Per calcolarla somma fra loro tutti i valori dei dati e poi dividi il totale per il numero (n) dei dati stessi.
- Considerando l’esempio dei voti (10, 8, 10, 8, 8, 4) ci sono 6 numeri nell’insieme. Quindi n=6.
-
3Somma fra loro i valori. Questo è il primo passaggio per ottenere la media aritmetica.
- Usiamo sempre i dati dei voti dell’esame: 10, 8, 10, 8, 8 e 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Questa è la somma dei voti che formano il campione.
- Controlla la somma una seconda volta per essere certo di non commettere errori.
-
4Dividi la somma per il numero di dati presenti nel campione (n). Questa divisione ti fornisce il valore medio dell’insieme.
- Considerando sempre l’esempio precedente (10, 8, 10, 8, 8, 4) sappiamo che ci sono sei voti, quindi n=6.
- La somma dei valori dei voti è 48 e dobbiamo dividerla per n per ottenere la media.
- 48:6 = 8
- Il valore medio dei voti ottenuti al test è 8.
Pubblicità
Trovare la Varianza
-
1La varianza è una variabile che rappresenta la distribuzione dei dati di un campione attorno al valore medio.
- Ti fornisce un’idea di quanto sono lontani i dati dalla media.
- I campioni con una varianza bassa sono composti da dati molto vicini al valore medio.
- I campioni con una varianza alta sono composti da dati che si distribuiscono molto lontano dalla media.
- La varianza, spesso, si utilizza per comparare la distribuzione di due insiemi di dati.
-
2Da ogni dato che compone l’insieme sottrai il valore medio. In questo modo comprendi quanto si discostano dalla media.
- Nell’esempio dei voti (10, 8, 10, 8, 8, 4) la media aritmetica è 8.
- 10 - 8 = 2; 8 - 8 = 0; 10 - 8 = 2; 8 - 8 = 0; 8 - 8 = 0 e 4 - 8 = -4.
- Ripeti la procedura per accertarti della correttezza dei calcoli. È fondamentale non commettere errori che porterebbero a un risultato sbagliato.
-
3Eleva al quadrato ogni differenza che hai appena calcolato. Per trovare la varianza del tuo campione, devi prima procedere a questo calcolo.
- Ricorda che da ogni dato dell’insieme (10, 8, 10, 8, 8, 4) hai sottratto il valore medio (8) trovando i seguenti valori: 2, 0, 2, 0, 0 e -4.
- Ora passa a elevare a seconda potenza i numeri che hai calcolato: 22; 02; 22; 02; 02; (-4)2 = 4, 0, 4, 0, 0 e 16.
- Controlla i calcoli prima di procedere al prossimo passaggio.
-
4Somma fra loro i quadrati appena calcolati.
- Quindi devi procedere a sommare fra loro: 4, 0, 4, 0, 0 e 16.
- Ricorda che hai inizialmente sottratto da ogni dato del tuo campione il valore medio e successivamente elevato a potenza di due ogni differenza: (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- La somma dei quadrati è 24.
-
5Dividi questo valore per (n-1)[1] . Ricorda che n è il numero dei dati presenti nel tuo insieme. Quest'ultimo calcolo ti fornirà la varianza.
- Procediamo con l’esempio dei risultati dell’esame (10, 8, 10, 8, 8, 4) in cui ci sono 6 dati. Quindi n=6.
- n-1 = 5.
- Ricorda che la somma dei quadrati è 24.
- 24 : 5 = 4,8
- La varianza dell’insieme è 4,8.
Pubblicità
Calcolare la Deviazione Standard
-
1Trova la varianza del tuo insieme. Hai bisogno di questo dato per calcolare la deviazione standard.
- Ricorda che la varianza ti mostra come i dati di un campione si distribuiscono attorno alla media aritmetica.
- La deviazione standard è in parte simile alla varianza.
- Se consideriamo sempre l’esempio dei risultati di un esame, sappiamo che la varianza è 4,8.
-
2Calcola la radice quadrata della varianza. In questo modo trovi la deviazione standard.
- Solitamente, almeno il 68% di tutti i campioni ricade all’interno di una deviazione standard dalla media.
- Ricorda che la varianza dell’esempio è 4,8.
- √4,8 = 2,19. La deviazione standard del campione di voti è 2,19.
- 5 dati su 6 (83%) del campione (10, 8, 10, 8, 8, 4) ricadono all’interno di una deviazione standard (2,19) dalla media.
-
3Ripassa i procedimenti di calcolo della media, della varianza e della deviazione standard. In questo modo puoi verificare la presenza di errori e riformulare la tua risposta.
- Quando esegui i calcoli e risolvi il problema è fondamentale scrivere tutti i passaggi, a prescindere dal fatto che stai usando una calcolatrice o meno.
- Se in fase di controllo trovi un valore differente, procedi con una terza verifica.
- Se non riesci a trovare l’errore, ricomincia tutto da capo.
Pubblicità
Informazioni su questo wikiHow
Per calcolare la deviazione standard, inizia ottenendo la media del campione di dati. Sottrai poi la media da tutti i valori del campione ed eleva al quadrato tutte le differenze. In seguito somma tutti i quadrati e dividi il risultato per n meno 1, in cui n è pari al numero di elementi presenti nel campione. Infine calcola la radice quadrata del numero per ottenere la deviazione standard. Per imparare a trovare la deviazione standard con un problema d'esempio, continua a leggere!


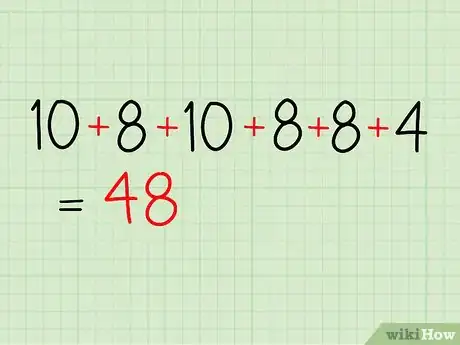
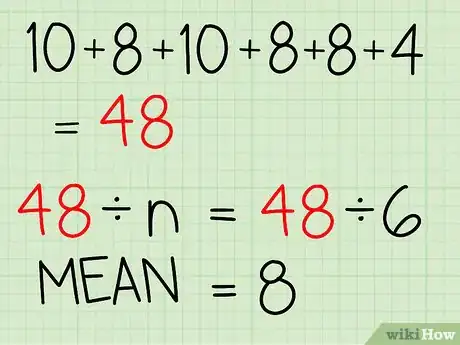












-to-Grams-(g)-Step-12-Version-4.webp)