wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 20 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Ci sono 8 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 64 905 volte
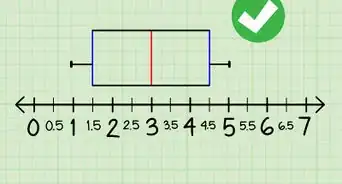
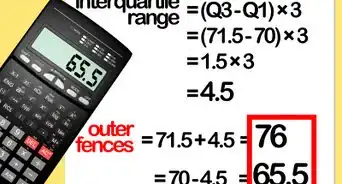
Lo scarto interquartile (in inglese IQR) viene usato in analisi statistica come aiuto per trarre delle conclusioni inerenti a una determinata serie di dati. Essendo in grado di escludere la maggior parte degli elementi anomali, l'IQR viene utilizzato spesso in relazione a un campione di dati per misurarne l'indice di dispersione. Prosegui nella lettura per scoprire come calcolarlo.
Passaggi
Lo Scarto Interquartile
-
1Come si usa l'IQR. Sostanzialmente l'IQR mostra la distribuzione o "dispersione" di un insieme di numeri.[1] Lo scarto interquartile si definisce come la differenza tra il terzo e il primo quartile di un insieme di dati. Il quartile inferiore o primo quartile viene normalmente indicato con Q1, mentre il quartile superiore o terzo quartile viene indicato con Q3, che tecnicamente si trova compreso fra il quartile Q2 e il quartile Q4.[2]
-
2Comprendi il significato di quartile. Per visualizzare fisicamente un quartile, dividi in quattro parti uguali una lista di numeri. Ognuna di queste porzioni di valori rappresenta un "quartile".[3] Prendiamo in considerazione il seguente campione di valori: 1, 2, 3, 4, 5, 6, 7, 8.
- I numeri 1 e 2 rappresentano il primo quartile o Q1.
- I numeri 3 e 4 rappresentano il primo quartile o Q2.
- I numeri 5 e 6 rappresentano il primo quartile o Q3.
- I numeri 7 e 8 rappresentano il primo quartile o Q4.
-
3Impara la formula. Per poter calcolare la differenza fra il quartile superiore e quello inferiore, ovvero calcolare lo scarto interquartile, hai la necessità di sottrarre il 25° percentile dal 75° percentile. La formula in oggetto è la seguente: IQR = Q3 – Q1.[4]Pubblicità
Ordinare il Campione di Dati
-
1Raggruppa i tuoi dati. Se devi apprendere come calcolare lo scarto interquartile per un esame scolastico, molto probabilmente, ti verrà fornito un insieme di dati già pronto e ordinato. Prendiamo come esempio il seguente campione di numeri: 1, 4, 5, 7, 10. È anche possibile che tu debba estrarre e ordinare i dati del tuo campione di valori direttamente dal testo del problema o da un qualche tipo di tabella. Assicurati che i dati forniti siano della stessa natura. Ad esempio, il numero di uova presenti in ogni nido della popolazione di uccelli usata come campione oppure il numero di posti auto riservati a ogni casa di un determinato quartiere.[5]
-
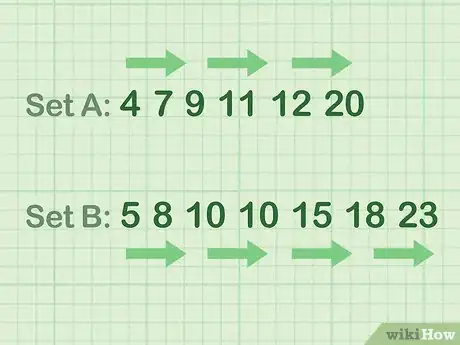
2Ordina i tuoi dati in ordine ascendente. In altre parole organizza l'insieme dei valori in modo che siano ordinati partendo dal più piccolo. Fai riferimento ai seguenti esempi:
- Campione di dati avente un numero pari di elementi (Gruppo A): 4, 7, 9, 11, 12, 20.
- Campione di dati avente un numero dispari di elementi (Gruppo B): 5, 8, 10, 10, 15, 18, 23.
-
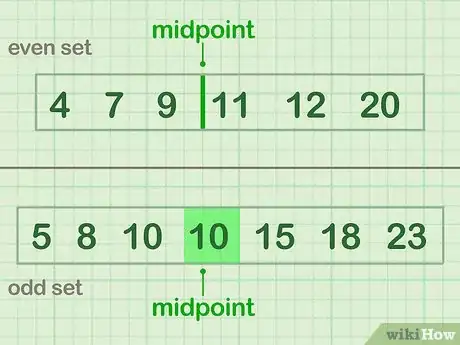
3Dividi il campione di dati a metà. Per farlo, devi prima individuare il punto medio del tuo insieme di valori, cioè il numero o l'insieme di numeri che si trovano esattamente al centro della distribuzione ordinata del campione in oggetto. Se stai osservando un insieme di valori numerici che contiene un numero dispari di elementi, devi scegliere esattamente l'elemento mediano. Al contrario, se stai osservando un insieme di valori numerici che contiene un numero pari di elementi il valore medio sarà a metà fra i due elementi mediani dell'insieme.
- Nel Gruppo A di esempio la mediana si trova fra 9 e 11: 4, 7, 9 | 11, 12, 20.
- Nel Gruppo B di esempio il valore mediano è (10): 5, 8, 10, (10), 15, 18, 23.
Pubblicità
Calcolare lo Scarto Interquartile
-
1Calcola la mediana relativa alla metà inferiore e superiore del tuo insieme di dati. La mediana è il valore medio o il numero che si trova al centro di una distribuzione ordinata di valori.[6] In questo caso non stai cercando il valore mediano dell'intero insieme di dati, ma stai cercando la mediana dei due sottogruppi in cui hai suddiviso il campione originario. Se hai un numero dispari di valori, nel calcolo della mediana non includere l'elemento mediano. Nel nostro esempio, quando calcoli la mediana del Gruppo B, non dovrai includere uno dei due numeri 10.[7]
- Gruppo A di esempio:
- Mediana del sottogruppo inferiore = 7 (Q1)
- Mediana del sottogruppo superiore = 12 (Q3)
- Gruppo B di esempio
- Mediana del sottogruppo inferiore = 8 (Q1)
- Mediana del sottogruppo superiore = 18 (Q3)
- Gruppo A di esempio:
-
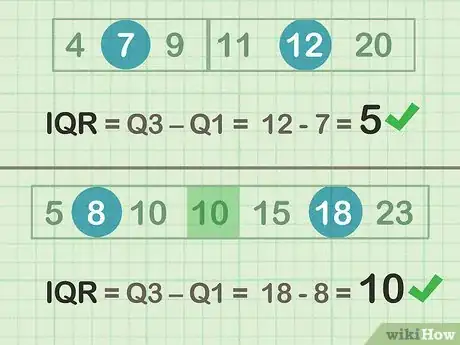
2Sapendo che IQR = Q3 - Q1, esegui la sottrazione. Adesso che conosciamo quanti numeri sono compresi fra il 25° e il 75° percentile, possiamo utilizzare questo dato per comprendere come sono distribuiti. Ad esempio, se un esame ha dato un risultato 100 e lo scarto interquartile relativo ai punteggi è 5, puoi dedurre che la maggior parte delle persone lo ha sostenuto avendo una comprensione molto simile della materia in oggetto perché i punteggi sono distribuiti in un intervallo ristretto di valori. Tuttavia, se l'IQR fosse 30, potresti iniziare a concentrarti sul perché alcune persone hanno realizzato un punteggio tanto alto e altre tanto basso.
- Gruppo A di esempio: 12 - 7 = 5
- Gruppo B di esempio: 18 - 8 = 10
Pubblicità
Consigli
- È importante capire e imparare a calcolare queste informazioni in autonomia, ma è anche giusto sapere che esistono degli strumenti online utilizzabili per controllare la correttezza del proprio lavoro.[8] Se stai imparando queste nozioni per sostenere un esame è meglio non fare troppo affidamento su questi strumenti automatici. Se durante un esame ti viene chiesto di calcolare lo scarto interquartile, devi saperlo fare senza l'aiuto di nessuno.
Riferimenti
- ↑ http://www.alcula.com/calculators/statistics/interquartile-range/
- ↑ http://www.mathwords.com/i/interquartile_range.htm
- ↑ https://www.mathsisfun.com/data/quartiles.html
- ↑ http://www.statisticshowto.com/calculators/interquartile-range-calculator/
- ↑ https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-data-statistics/cc-6th/e/calculating-the-interquartile-range--iqr-
- ↑ http://www.mathgoodies.com/lessons/vol8/median.html
- ↑ http://www.bbc.co.uk/schools/gcsebitesize/maths/statistics/representingdata3hirev4.shtml
- ↑ https://www.easycalculation.com/statistics/inter-quartile-range.php





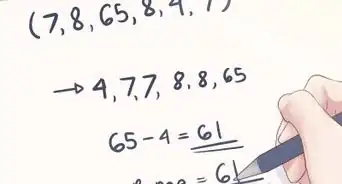



-to-Grams-(g)-Step-12-Version-4.webp)