wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 45 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 30 901 volte
I fattori di un numero sono le cifre che, moltiplicate fra loro, danno come prodotto il numero stesso. Per comprendere meglio il concetto, puoi considerare ogni numero come il risultato della moltiplicazione dei suoi fattori. Imparare a scomporre un numero in fattori primi è un’abilità matematica importante che ti sarà utile non solo per i problemi di aritmetica, ma anche per l’algebra, l’analisi matematica e via discorrendo. Continua a leggere per saperne di più.
Passaggi
Scomporre in Fattori gli Interi di Base
-
1Scrivi il numero in esame. Per iniziare la scomposizione puoi usare qualunque numero ma, per i nostri scopi didattici, usiamo un semplice intero. Un intero è un numero senza componente decimale o frazionale (tutti gli interi possono essere negativi o positivi).
- Scegliamo il numero 12. Scrivilo su un foglio.
-
2Trova due numeri che, moltiplicati fra loro, diano il numero di origine. Ogni numero intero può essere riscritto sotto forma di prodotto di altri due interi. Anche i numeri primi possono essere considerati il prodotto di se stessi e 1. Trovare i fattori richiede un ragionamento a "ritroso", in pratica devi chiederti: “quale moltiplicazione dà come risultato il numero in esame?”.
- Nell’esempio che abbiamo considerato, 12 ha molti fattori. 12x1; 6x2; 3x4 danno tutti come risultato 12. Quindi possiamo affermare che i fattori di 12 sono 1, 2, 3, 4, 6 e 12. Sempre per i nostri scopi, usiamo i fattori 6 e 2.
- I numeri pari sono particolarmente semplici da scomporre perché 2 è un fattore. Infatti 4 = 2x2; 26 = 2x13 e così via.
-
3Verifica se i fattori che hai individuato sono ulteriormente scomponibili. Molti numeri, soprattutto quelli grandi, possono essere scomposti molte volte. Quando trovi due fattori di un numero che sono a loro volta il prodotto di altri fattori più piccoli, puoi provvedere alla scomposizione. In base al tipo di problema che devi risolvere, questo passaggio può essere utile o meno.
- Nel nostro esempio, abbiamo ridotto 12 come 2x6. Anche 6 possiede i suoi fattori (3x2). Quindi puoi riscrivere la scomposizione come 12 = 2x(3x2).
-
4Ferma la scomposizione quando raggiungi dei numeri primi. Questi sono dei numeri divisibili solo per 1 e per se stessi. Ad esempio 1, 2, 3, 5, 7, 11, 13 e 17 sono tutti numeri primi. Quando hai scomposto un numero in fattori primi, non puoi andare oltre.
- Nell’esempio del numero 12, abbiamo raggiunto la scomposizione di 2x(3x2). I numeri 2 e 3 sono tutti primi, se volessi procedere a un’ulteriore scomposizione, dovresti scrivere (2x1)x[(3x1)x(2x1)] che non è utile e deve essere evitata.
-
5I numeri negativi si scompongono con lo stesso criterio. L’unica differenza è che i fattori devono essere moltiplicati in maniera tale da ottenere un numero negativo; ciò significa che una quantità dispari di fattori deve essere negativa.
- Scomponi -60 in fattori primi:
- -60 = -10x6
- -60 = (-5 x 2) x 6
- -60 = (-5 x 2) x (3 x 2)
- -60 = -5 x 2 x 3 x 2. Nota che la presenza di una quantità dispari di cifre negative porta a un prodotto negativo. Se avessi scritto: 5 x 2 x -3 x -2 avresti ottenuto 60.
Pubblicità - Scomponi -60 in fattori primi:
Procedura per Scomporre i Numeri Grandi
-
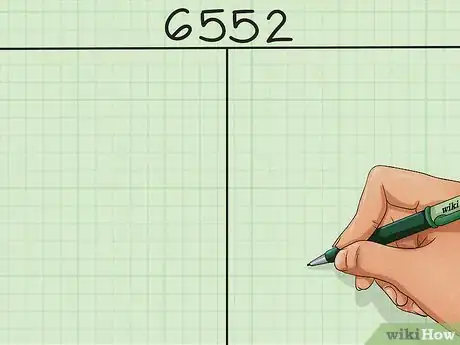
1Scrivi il numero sopra una tabella a due colonne. Sebbene non sia affatto difficile scomporre in fattori un numero piccolo, con i numeri molto grandi è un po’ più complesso. La maggior parte di noi avrebbe qualche difficoltà a scomporre a mente un numero di 4 o 5 cifre in fattori primi. Per fortuna, una tabella ci semplifica il lavoro. Scrivi il numero sopra una tabella a forma di “T” così da formare due colonne. Questa tabella ti aiuta a registrare la lista dei fattori.
- Per i nostri scopi scegliamo un numero a 4 cifre: 6552.
-
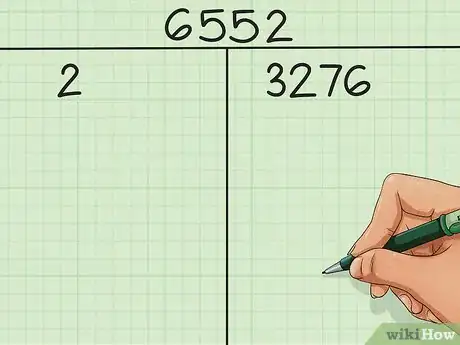
2Dividi il numero per il minimo fattore primo. Devi trovare il fattore minimo (oltre a 1) che divide il numero senza produrre resto. Scrivi il primo fattore nella colonna di sinistra e il quoziente della divisione nella colonna di destra. Come abbiamo già detto, i numeri pari sono semplici da scomporre perché il minimo fattore primo è 2. I numeri dispari, invece, possono avere un minimo fattore diverso.
- Ritornando all’esempio di 6552, che è pari, sappiamo che 2 è il minimo fattore primo. 6552÷ 2 = 3276. Nella colonna di sinistra scriverai 2 e in quella di destra 3276.
-
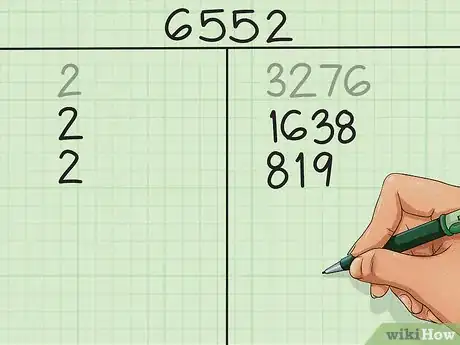
3Continua seguendo questa logica. Ora devi scomporre il numero che si trova nella colonna di destra cercando sempre il suo minimo fattore primo. Scrivi il fattore nella colonna di sinistra sotto al primo fattore che hai trovato e il risultato della divisione nella colonna di destra. A ogni passaggio il numero a destra diventa sempre più piccolo.
- Continuiamo nel nostro calcolo. 3276 ÷ 2 = 1638, quindi nella colonna di sinistra scriverai un altro 2 e nella colonna di destra 1638. 1638 ÷ 2 = 819, quindi scrivi un terzo 2 e 819, seguendo sempre la stessa logica.
-
4Occupati dei numeri dispari per cercare i loro minimi fattori primi. I numeri dispari sono più difficili da scomporre, perché non sono automaticamente divisibili per un determinato numero primo. Quando ottieni un numero dispari, devi provare con divisori diversi da due, come 3, 5, 7, 11 e così via finché ottieni un quoziente senza resto. A quel punto hai trovato il minimo fattore primo.
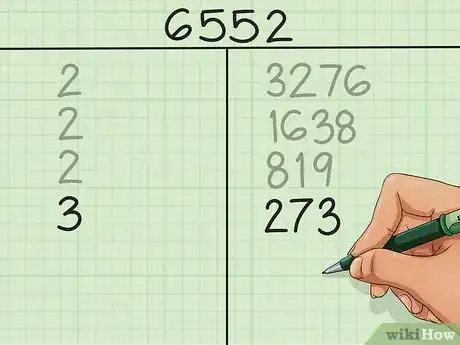
- Nel nostro esempio precedente, hai raggiunto il numero 819. Si tratta di un valore dispari, quindi 2 non può essere un suo fattore. Devi provare con il numero primo successivo: 3. 819 ÷ 3 = 273 senza alcun resto, quindi scrivi 3 nella colonna di sinistra e 273 in quella di destra.
- Quando cerchi i fattori, dovresti provare tutti i numeri primi fino alla radice quadrata del fattore più grande trovato fino ad ora. Se nessuno dei fattori è divisore del numero, allora è probabile che si tratti di un numero primo e il processo di scomposizione è da considerarsi terminato.
-
5Continua finché ottieni 1 come quoziente. Procedi nelle divisioni cercando di volta in volta il minimo fattore primo finché nella colonna di destra raggiungi un numero primo. A questo punti dividilo per se stesso e scrivi "1" nella colonna di destra.
- Completa la scomposizione. Leggi quanto segue per i dettagli:
- Dividi ancora per 3: 273 ÷ 3 = 91 senza resto, quindi scrivi 3 e 91.
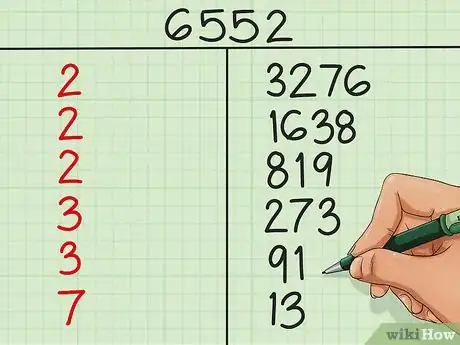
- Prova a dividere ancora per 3: 91 non è divisibile per 3 né per 5 (il fattore primo successivo a 3) ma troverai che 91 ÷ 7 = 13 senza resto, quindi scrivi 7 e 13.
- Ora prova a dividere 13 per 7: non è possibile ottenere un quoziente senza resto. Passa al fattore primo successivo, 11. Anche in questo caso 13 non è divisibile per 11. Alla fine troverai che 13 ÷ 13 = 1. Quindi completa la tabella scrivendo 13 e 1. Hai completato la scomposizione.
- Completa la scomposizione. Leggi quanto segue per i dettagli:
-
6Usa i numeri della colonna a sinistra come fattori del numero originale oggetto del problema. Quando hai raggiunto la cifra 1 nella colonna di destra, hai terminato. In altre parole, tutti i numeri presenti nella colonna di sinistra, se moltiplicati fra loro, danno come prodotto il numero iniziale. Se ci sono dei fattori che si presentano più volte, allora puoi usare la notazione esponenziale per risparmiare spazio. Ad esempio se la lista di fattori presenta quattro volte il numero 2, allora puoi scrivere 24 al posto di 2x2x2x2.
- Il numero che abbiamo preso in considerazione è scomponibile come segue: 6552 = 23 x 32 x 7 x 13. Questa è la scomposizione completa in fattori primi di 6552. A prescindere dall’ordine che segui per svolgere la moltiplicazione, il prodotto sarà sempre 6552.
Pubblicità
Consigli
- È importante anche il concetto di numero primo: un numero che ha solo due fattori, 1 e se stesso. 3 è un numero primo perché i suoi unici fattori sono 1 e 3. 4, invece, ha 2 tra i suoi fattori. Un numero che non è primo è detto composto (il numero 1, tuttavia, non è considerato né primo né composto: si tratta di un caso speciale).
- I numeri primi più piccoli sono 2, 3, 5, 7, 11, 13, 17, 19 e 23.
- Ricorda che un numero è fattore di un altro maggiore se lo "divide perfettamente" senza resto. Ad esempio 6 è fattore di 24 perché 24 ÷ 6 = 4 senza alcun resto; mentre 6 non è fattore di 25.
- Ricorda che ci riferiamo solo ai cosiddetti "numeri naturali": 1, 2, 3, 4, 5... Non tratteremo i numeri negativi o le frazioni, per i quali sono necessari articoli specifici.
- Alcuni numeri possono essere scomposti in modi più rapidi, ma questo metodo funziona sempre e, inoltre, avrai i fattori primi elencati in ordine crescente.
- Se la somma delle cifre che compongono un certo numero è un multiplo di 3, allora 3 è un fattore di quel numero. Ad esempio: 819 = 8+1+9 = 18, 1+8 = 9. 3 è un fattore di 9, quindi è un fattore di 819.
Avvertenze
- Non fare del lavoro inutile. Una volta che hai eliminato un fattore candidato, non lo devi provare di nuovo. Una volta deciso che 2 non era un fattore di 819, non abbiamo dovuto considerarlo ancora nel resto della procedura.
Cose che ti Serviranno
- Un foglio
- Qualcosa per scrivere, preferibilmente una matita e una gomma
- Una calcolatrice (facoltativo)
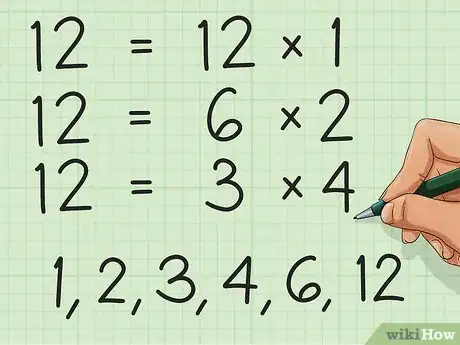
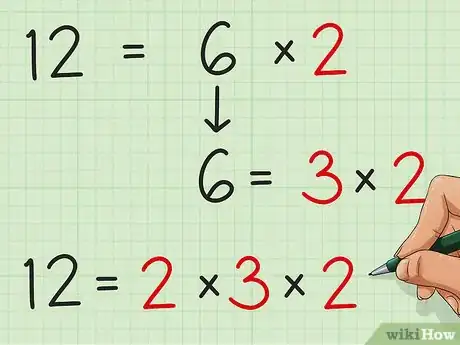

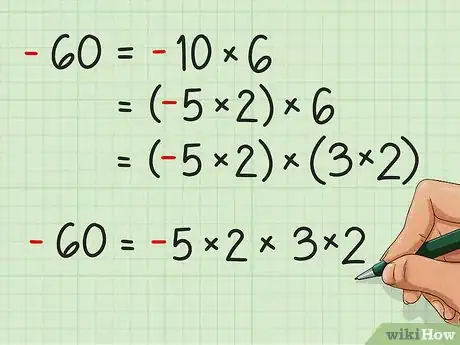

-Step-31-Version-2.webp)






-to-Grams-(g)-Step-12-Version-4.webp)



-Step-31-Version-2.webp)