Come Usare un Regolo Calcolatore

Info sull'Autore

Per coloro che non sanno come usarlo, il regolo calcolatore ha l’aspetto di una riga progettata da Picasso. Ci sono almeno tre scale differenti, e la maggior parte di esse non indicano dei valori in senso assoluto. Ma dopo che imparerai a conoscere questo strumento capirai il motivo per cui si è rivelato così utile nel corso dei secoli, prima dell’avvento delle calcolatrici tascabili. Allinea i numeri sulla scala e potrai moltiplicare due fattori qualsiasi, con un procedimento meno complicato rispetto a quello utilizzato con carta e penna.

Parte 1

Parte 1 di 4:

Comprendere i Regoli Calcolatori

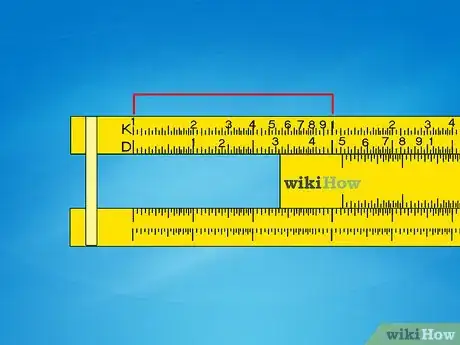
1
Nota l’intervallo tra i numeri. A differenza di una riga normale, sul regolo calcolatore i numeri non sono equidistanti; al contrario, sono distanziati usando una particolare formula logaritmica, più addensati su un lato rispetto che sull’altro. Ciò ti permette di allineare le scale per ottenere il risultato di operazioni matematiche, come descritto qui di seguito.
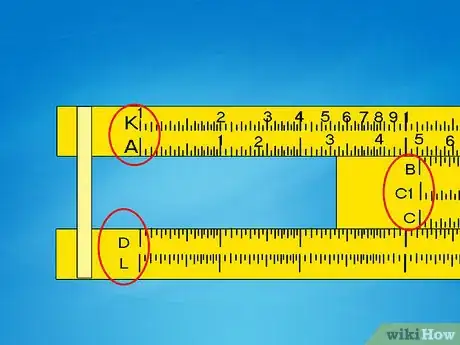
2
Cerca i nomi delle scale. Ciascuna scala dovrebbe riportare una lettera o un simbolo a sinistra o a destra. Questa guida presume che il tuo regolo calcolatore usi le scale più comuni:^{[1]
X
Fonte di ricerca}
- Le scale C e D hanno l’aspetto di una singola riga lineare, leggendo da sinistra verso destra. Queste sono chiamate scale a “decina singola”.
- Le scale A e B sono scale a “decina doppia”. Ciascuna ha due righe più piccole allineate.
- La scala K è a decina tripla, ovvero con tre righe allineate. Non è presente in tutti i modelli.
- Le scale C| e D| sono uguali a quelle C e D, ma lette da destra a sinistra. Queste solitamente sono di colore rosso, ma non sono presenti in tutti i modelli.
3
Cerca di comprendere le divisioni della scala. Dai uno sguardo alle linee verticali della scala C o D, e abituati a leggerle:
- I numeri primari sulla scala iniziano dall’1 sull’estremità sinistra, continuano fino al 9, e terminano con un altro 1 sull’estremità destra. Di solito sono tutti segnati.
- Le divisioni secondarie, segnate dalle linee verticali al secondo posto in ordine di altezza dividono ciascun numero primario per 0,1. Non confonderti se sono chiamati “1, 2, 3”; ricordati che essi in realtà rappresentano “1,1; 1,2; 1,3” e così via.
- Di solito ci sono divisioni più piccole, che rappresentano incrementi dello 0,02. Presta molta attenzione, poiché potrebbero scomparire alla fine della scala, dove i numeri si avvicinano tra di essi.
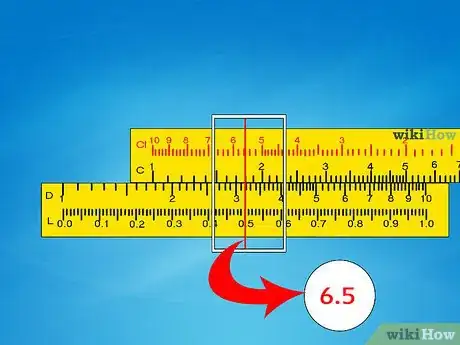
4
Non pretendere di ottenere risultati precisi. Spesso dovrai fare la “migliore ipotesi” quando leggi una scala in cui il risultato non si trova esattamente su una linea. I regoli calcolatori sono utilizzati per calcoli veloci, non per scopi che richiedono una precisione estrema.
- Per esempio, se il risultato si trova tra 6,51 e 6,52, scrivi il valore più vicino. Se non lo conosci, scrivi 6,515.
Pubblicità

Parte 2

Parte 2 di 4:

Moltiplicare i Numeri

1
Scrivi i numeri che vuoi moltiplicare.
- Nell’esempio 1 di questa sezione calcoleremo 260 x 0,3.
- Nell’esempio 2 calcoleremo 410 x 9. Il secondo esempio risulta più complicato del primo, pertanto dovresti eseguire prima questo.
2
Sposta i punti decimali per ciascun numero. Il regolo calcolatore comprende solo i numeri tra 1 e 10. Sposta il punto decimale in ciascun numero che moltiplichi, affinché si trovi tra questi valori. Dopo che l’operazione sarà completata, sposteremo il punto decimale al posto giusto, come sarà descritto al termine di questa sezione.
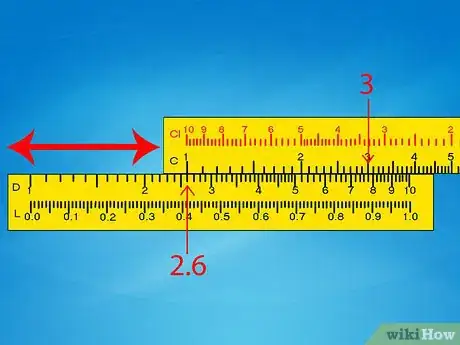
- Esempio 1: per calcolare 260 x 0,3, inizia da 2,6 x 3.
- Esempio 2: per calcolare 410 x 9, inizia da 4,1 x 9.
3
Trova il numero più piccolo sulla scala D, poi fai scivolare la scala C su di essa. Trova il numero più piccolo sulla scala D. Fai scivolare la scala C affinché il numero 1 all’estrema sinistra (chiamato indice sinistro) sia allineato con quel numero.
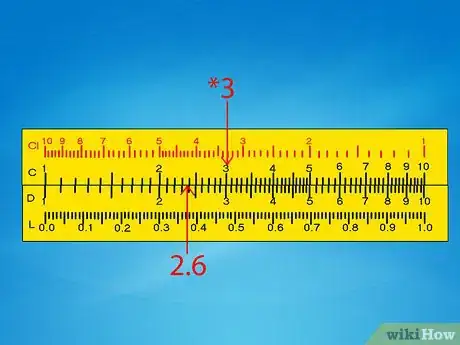
- Esempio 1: fai scorrere la scala C affinché l’indice sinistro sia in linea con 2,6 sulla scala D.
- Esempio 2: fai scorrere la scala C affinché l’indice sinistro sia allineato con 4,1 sulla scala D.
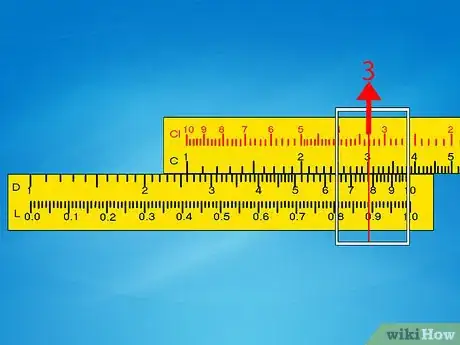
4
Fai scivolare il corsoio sul secondo numero della scala C. Il corsoio è l’oggetto metallico che scivola lungo tutta la riga. Allinealo con il secondo fattore della tua moltiplicazione sulla scala C. Il corsoio indicherà il risultato sulla scala D. Se non riesce a scivolare fino a quel punto, vai al passaggio successivo.
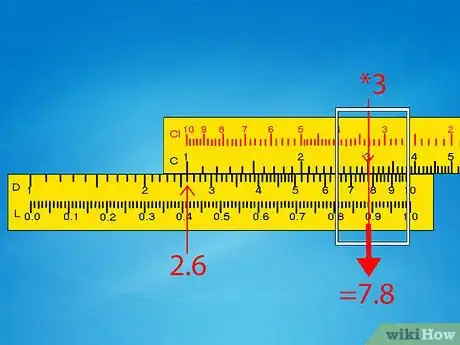
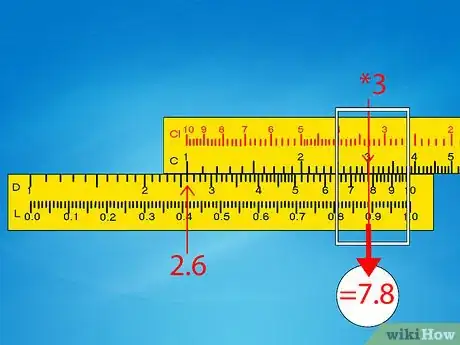
- Esempio 1: fai scorrere il corsoio affinché indichi il 3 sulla scala C. In questa posizione dovrebbe indicare anche 7,8 sulla scala D. Vai direttamente al passaggio dell’approssimazione.
- Esempio 2: cerca di far scorrere il corsoio affinché indichi il 9 sulla scala C. Per la maggior parte dei regoli calcolatori ciò non sarà possibile, oppure il corsoio indicherà il vuoto fuori della scala D. Leggi il passaggio successivo per capire come risolvere questo problema.
5
Se il corsoio non scorre fino al risultato, usa l’indice destro. Se è bloccato da un dente di arresto al centro del regolo calcolatore, oppure se il risultato è fuori scala, adotta un approccio leggermente diverso. ^{[2]
X
Fonte di ricerca} Fai scorrere la scala C affinché l’indice destro oppure l’1 sull’estrema destra sia posizionato sul fattore maggiore della moltiplicazione. Fai scorrere il corsoio nella posizione dell’altro fattore sulla scala C e leggi il risultato sulla scala D.
- Esempio 2: fai scorrere la scala C affinché l’1 all’estrema destra sia allineato con il 9 sulla scala D. Fai scorrere il corsoio su 4,1 sulla scala C. Il corsoio indica tra 3,68 e 3,7 sulla scala D, pertanto il risultato dovrà essere 3,69 circa.
6
Usa l’approssimazione per trovare il punto decimale corretto. Indipendentemente dalla moltiplicazione che esegui, il risultato sarà sempre letto sulla scala D, che mostra solo numeri da 1 a 10. Dovrai servirti dell’approssimazione e del calcolo mentale per determinare dove mettere il punto decimale nel tuo risultato reale.
- Esempio 1: il nostro problema originale era 260 x 0,3 e il regolo calcolatore ci ha restituito un risultato pari a 7,8. Arrotonda il risultato originale e risolvi l’operazione nella tua mente: 250 x 0,5 = 125. È più vicino a 78 anziché a 780 o a 7,8, pertanto la risposta è 78.
- Esempio 2: il nostro problema originale era 410 x 9 e abbiamo letto 3,69 sul regolo calcolatore. Considera il problema originale come 400 x 10 = 4000. Il risultato più vicino che possiamo raggiungere spostando il punto decimale è 3690, pertanto questo dovrà essere la risposta.
Pubblicità

Parte 3

Parte 3 di 4:

Calcolare i Quadrati e i Cubi

1
Usa le scale D e A per calcolare i quadrati. Queste due scale di solito sono fissate in un punto. Fai semplicemente scorrere il corsoio metallico sul valore della scala D e il valore A sarà il quadrato. ^{[3]
X
Fonte di ricerca} Proprio come un’operazione di matematica, dovrai determinare da solo la posizione del punto decimale.
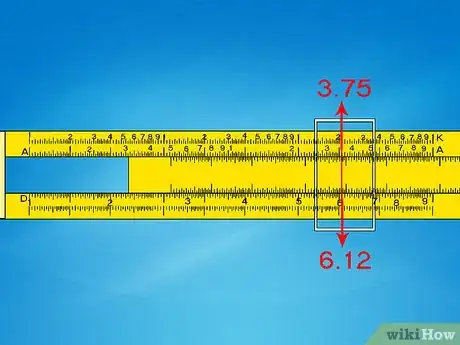
- Per esempio, per risolvere 6,1²,fai scorrere il corsoio su 6,1 sulla scala D. Il valore A corrispondente è circa 3,75.
- Approssima 6,1² a 6 x 6 = 36. Posiziona il punto decimale per ottenere un risultato vicino a questo valore: 37,5.
- Nota che la risposta esatta è 37,21. Il risultato del regolo calcolatore è meno preciso dell’1% rispetto alle situazioni di vita reale.
2
Usa le scale D e K per calcolare i cubi. Hai appena visto come la scala A, che è una scala D ridotta a mezza scala, ti consente di trovare i quadrati dei numeri. Allo stesso modo la scala K, che è una scala D ridotta a un terzo, ti permette di calcolare i cubi. Fai scorrere semplicemente il corsoio a un valore D e leggi il risultato sulla scala K. Usa l’approssimazione per posizionare il decimale.
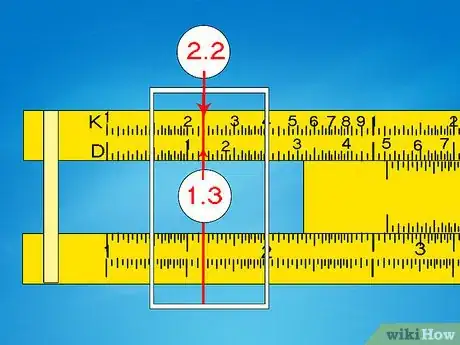
- Per esempio, per calcolare 130³, fai scorrere il corsoio verso 1,3 sul valore D. Il valore K corrispondente è 2,2. Poiché 100³ = 1 x 10⁶, e 200³ = 8 x 10⁶, sappiamo che il risultato deve essere tra di essi. Deve essere 2,2 x 10⁶, oppure 2.200.000.
Pubblicità

Parte 4

Parte 4 di 4:

Calcolare le Radici Quadrate e Cubiche

1
Converti il numero in notazione scientifica prima di calcolare una radice quadrata. Come sempre, il regolo calcolatore comprende solo valori da 1 a 10, pertanto dovrai scrivere il numero in notazione scientifica prima di trovare la sua radice quadrata.
- Esempio 3: per trovare √(390), scrivilo come √(3,9 x 10²).
- Esempio 4: per trovare √(7100), scrivilo come √(7,1 x 10³).
2
Individua quale lato della scala A usare. Per trovare la radice quadrata di un numero, il primo passo è far scorrere il corsoio su quel numero sulla scala A. Tuttavia, poiché la scala A è stampata due volte, dovrai decidere quale usare prima ^{[4]
X
Fonte di ricerca}. Per fare ciò, segui queste regole:
- Se l’esponente nella tua notazione scientifica è pari (come ² nell’esempio 3), usa il lato sinistro della scala A (la prima decina).
- Se l’esponente nella notazione scientifica è dispari (come ³ nell’esempio 4), usa il lato destro della scala A (la seconda decina).
3
Fai scorrere il corsoio sulla scala A. Ignorando per il momento l’esponente 10, fai scorrere il corsoio lungo la scala A verso il numero con cui hai terminato.
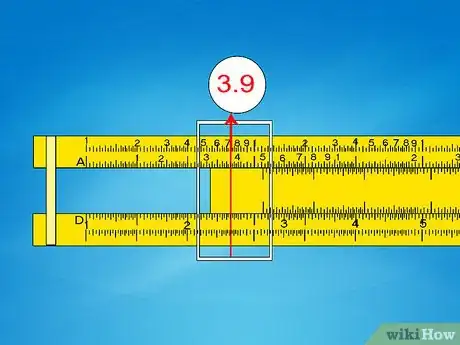
- Esempio 3: per trovare √(3,9 x 10²), fai scorrere il corsoio su 3,9 sulla scala A di sinistra (devi usare la scala sinistra, perché l’esponente è pari, come descritto in precedenza).
- Esempio 4: per trovare √(7,1 x 10³), fai scorrere il corsoio su 7,1 sulla scala A di destra (devi usare la scala destra perché l’esponente è dispari).
4
Determina il risultato dalla scala D. Leggi il valore D indicato dal corsoio. Aggiungi "x10ⁿ" a questo valore. Per calcolare n, prendi la potenza originale di 10, arrotonda per difetto al numero pari più vicino e dividi per 2.
- Esempio 3: il valore D corrispondente ad A = 3,9 è circa 1,975. Il numero originale nella notazione scientifica aveva 10²; 2 è già pari, pertanto dividi per 2 per ottenere 1. Il risultato finale è 1,975 x 10¹ = 19,75.
- Esempio 4: il valore D corrispondente ad A = 7,1 è circa 8,45. Il numero originale nella notazione scientifica aveva 10³, quindi arrotonda 3 al numero pari più vicino, 2, dopo dividi per 2 per ottenere 1. Il risultato finale è 8,45 x 10¹ = 84,5
5
Usa un procedimento simile sulla scala K per trovare le radici cubiche. Il passaggio più importante è individuare quale tra le scale K utilizzare. Per fare ciò dividi il numero delle cifre del tuo numero per 3 e trova il resto. Se il resto è 1, usa la prima scala. Se è 2, usa la seconda scala. Se è 3, usa la terza scala (un altro sistema per fare ciò è contare ripetutamente dalla prima alla terza scala, finché raggiungerai il numero di cifre nel tuo risultato).^{[5]
X
Fonte di ricerca}
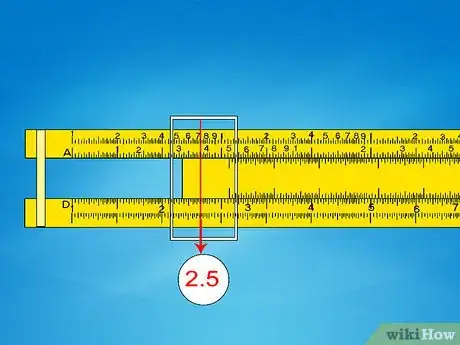
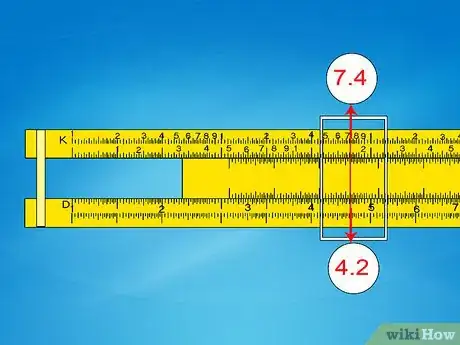
- Esempio 5: per trovare la radice cubica di 74.000, prima conta il numero delle cifre (5), dividi per 3 e trova il resto (1 resto 2). Siccome il resto è 2, usa la seconda scala. (Alternativamente, conta le scale cinque volte: 1-2-3-1-2).
- Fai scorrere il corsoio verso 7,4 sulla seconda scala K. Il valore D corrispondente è approssimativamente 4,2.
- Poiché 10³ è minore di 74.000, ma 100³ è maggiore di 74.000, il risultato deve essere tra 10 e 100. Sposta il punto decimale per ottenere 42.
Pubblicità

Consigli

Ci sono altre funzioni che puoi calcolare con il regolo calcolatore, specialmente se comprende scale logaritmiche, scale per calcoli trigonometrici, o altre scale speciali. Cimentati da solo oppure svolgi delle ricerche in rete.
Puoi usare la moltiplicazione per effettuare la conversione tra due unità di misura. Per esempio, poiché un pollice corrisponde a 2,54 cm, per convertire 5 pollici in centimetri è sufficiente moltiplicare 5 x 2,54.
La precisione di un regolo calcolatore dipende dal numero delle divisioni sulle scale. Più è lungo, più risulta preciso.