wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 15 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 88 575 volte
Un prisma è una figura geometrica solida con due estremità di base identiche e tutte le facce piane. Il prisma prende il nome dalla sua base: ad esempio, se è un triangolo, il solido è chiamato "prisma triangolare". Per trovare il volume di un prisma, devi solo calcolare l'area della sua base - la parte più complessa di tutto il procedimento - e moltiplicarla per l'altezza. Ecco come calcolare il volume di una serie di prismi.
Passaggi
Calcolare il Volume di un Prisma Triangolare
-
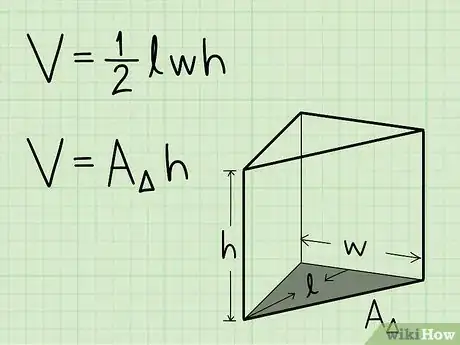
1Appuntati la formula per trovare il volume di un prisma triangolare. La formula è semplicemente V = 1/2 x lunghezza x larghezza x altezza. Tuttavia puoi anche usare questa:V = area di base x altezza solido. L'area di un triangolo si trova moltiplicando 1/2 della base per l'altezza.
-
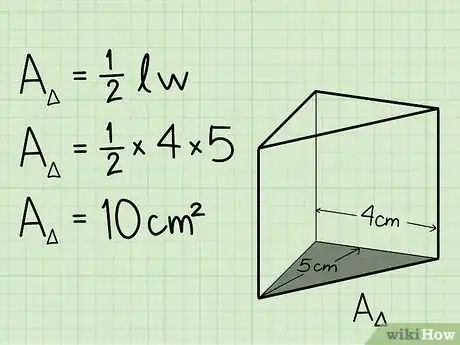
2Trova l'area della faccia di base. Per calcolare il volume di un prisma triangolare, è necessario trovare prima l'area della base, come indicato nel punto precedente.[1]
- Esempio: se l'altezza della base triangolare è di 5 cm e la base è 4 cm, allora l'area della base è 1/2 x 5 cm x 4 cm, che è 10 cm2.
-
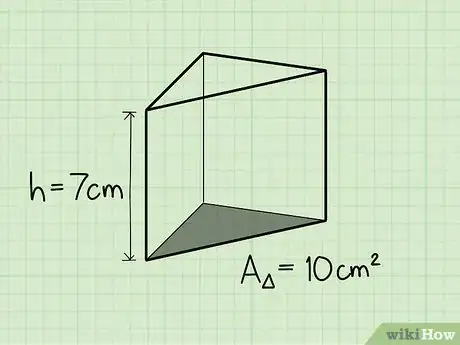
3Trova l'altezza. Supponiamo che l'altezza di questo prisma triangolare sia 7 cm.
-
4Moltiplica l'area della base triangolare per l'altezza e avrai il volume del prisma triangolare.
- Esempio: 10 cm2 x 7 cm = 70 cm3.
-
5Metti la tua risposta in unità cubiche. Devi sempre utilizzare unità cubiche quando calcoli il volume, perché stai lavorando con oggetti tridimensionali. La risposta finale è di 70 cm3.Pubblicità
Calcolare il Volume di un Cubo
-
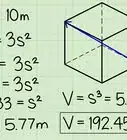
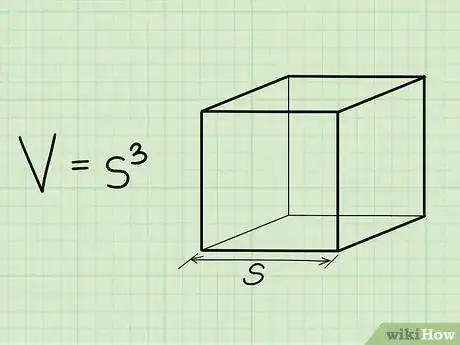
1Scrivi la formula per trovare il volume di un cubo. La formula è semplicemente V = spigolo3.Un cubo è un prisma avente le tre dimensioni uguali.[2]
-
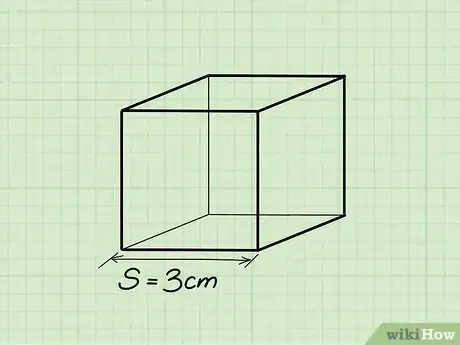
2Trova la lunghezza di uno spigolo del cubo. Tutti gli spigoli sono uguali, quindi non importa quale scegli.
- Esempio: Spigolo = 3 cm.
-
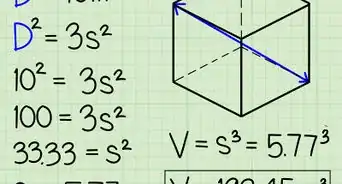
3Mettilo al cubo: basta moltiplicare il numero per se stesso, trovando il quadrato, e ancora una volta per se stesso. Il cubo di "a" è "a x a x a", ad esempio. Poiché tutte le dimensioni del cubo sono uguali, moltiplicando due spigoli qualsiasi avrai l'area della base e qualsiasi terzo spigolo potrebbe rappresentare l'altezza del solido.
- Esempio: 3 cm3 = 3 cm * 3 cm * 3 cm = 27 cm3.
-
4Metti la tua risposta in unità cubiche: il risultato finale è 125 cm3.Pubblicità
Calcolare il Volume di un Prisma Rettangolare
-
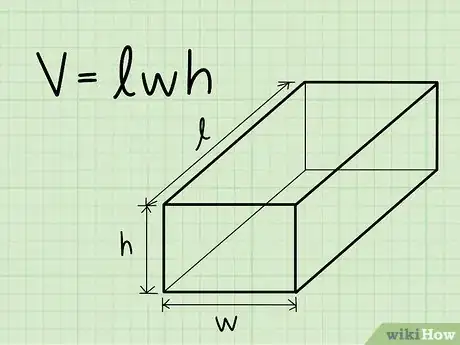
1Scrivi la formula per trovare il volume di un prisma rettangolare. La formula è semplicemente V = lunghezza x larghezza x altezza. Un prisma rettangolare è caratterizzato da un rettangolo di base.
-
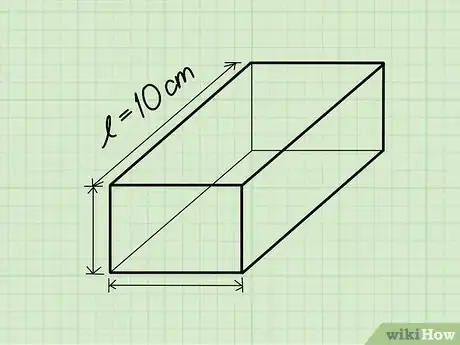
2Trova la lunghezza. La lunghezza è il lato maggiore del rettangolo sulla faccia superiore o inferiore del solido.
- Esempio: Lunghezza = 10 cm.
-
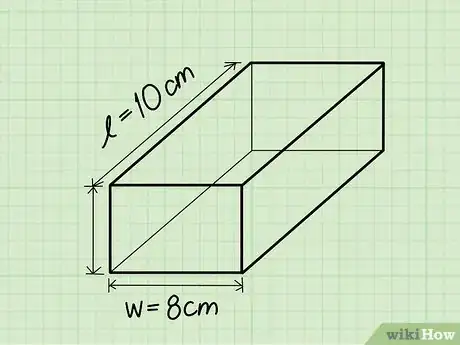
3Trova la larghezza. La larghezza del prisma rettangolare è il lato minore del rettangolo di base.
- Esempio: Larghezza = 8 cm.
-
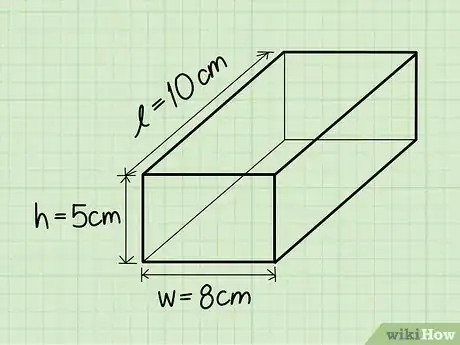
4Trova l'altezza. L'altezza è la parte del prisma rettangolare che si innalza. Si può immaginare l'altezza del prisma rettangolare come la parte che estende un rettangolo posto in un piano e lo rende tridimensionale.
- Esempio: Altezza = 5 cm.
-
5Moltiplica la lunghezza, la larghezza e l'altezza. Le puoi moltiplicare in qualsiasi ordine per ottenere lo stesso risultato. Utilizzando questo metodo, essenzialmente trovi l'area della base rettangolare (10 x 8) e la riporti tante volte quante sono espresse dall'altezza (5).
- Esempio: 10 cm x 8 cm x 5 cm = 400 cm3
-
6Metti la tua risposta in unità cubiche. La risposta finale è 400 cm3Pubblicità
Calcolare il Volume di un Prisma Trapezoidale
-
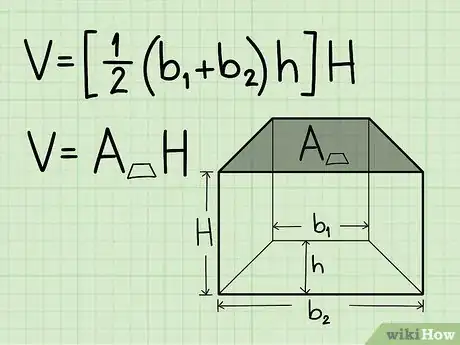
1Scriva la formula per calcolare il volume di un prisma trapezoidale. La formula è: V = [1/2 x (base1 + base2) x altezza] x altezza del solido. Si deve utilizzare la prima parte di questa formula per trovare l'area della base, un trapezio, prima di proseguire.[3]
-
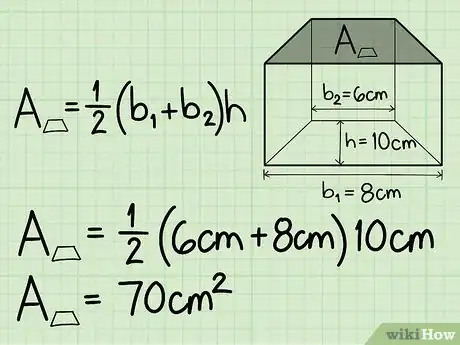
2Calcola l'area del trapezio. Per fare questo, è sufficiente sostituire le due basi e l'altezza della base trapezoidale nella prima parte della formula.
- Supponiamo che base1 = 8 cm, base2 = 6 cm e altezza = 10 cm.
- Esempio: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm2
-
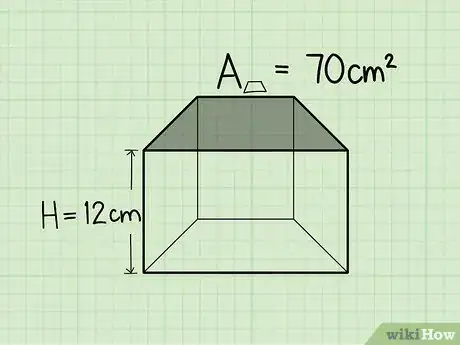
3Trova l'altezza del prisma trapezoidale: supponiamo sia 12 cm.
-
4Moltiplica l'area di base per l'altezza.
- 80 cm2 x 12 cm = 960 cm3.
-
5Metti la tua risposta in unità cubiche. La risposta finale è 960 cm3.Pubblicità
Calcolare il Volume di un Prisma Pentagonale Regolare
-
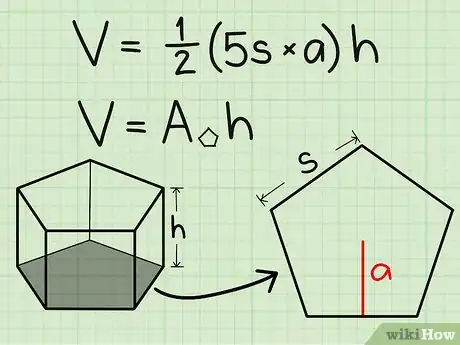
1Scrivi la formula per trovare il volume di un prisma pentagonale regolare. La formula è V = [1/2 x 5 x lato x apotema] x altezza del prisma. È possibile utilizzare la prima parte della formula per trovare l'area del pentagono. Si tratta di trovare l'area di cinque triangoli che compongono un poligono regolare. Il lato è semplicemente la larghezza di un triangolo, mentre l'apotema è l'altezza di uno dei triangoli. Moltiplica per 1/2 per trovare l'area di un triangolo e poi moltiplicare questo risultato per 5, perché sono i 5 triangoli che compongono il pentagono.[4]
- Per trovare l'apotema utilizzando formule trigonometriche, puoi effettuare ulteriori ricerche.[5]
-
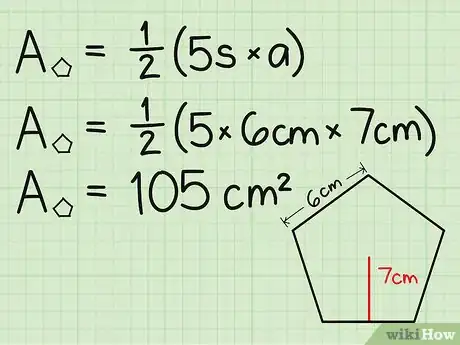
2Calcola l'area del pentagono. Supponiamo che il lato sia 6 cm e che la lunghezza dell'apotema sia 7 cm. Basta inserire questi numeri nella formula:
- A = 1/2 x 5 x lato x apotema
- A = 1/2 x 5 x 6 cm x 7 cm = 105 cm2.
-
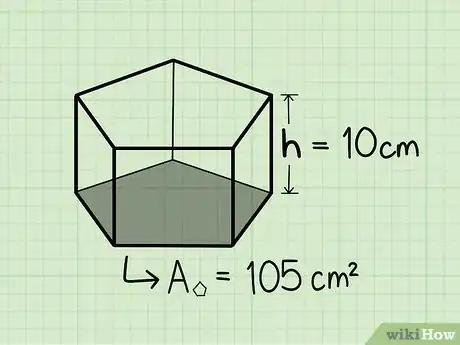
3Trova l'altezza del prisma. Supponiamo che sia 10 cm.
-
4Moltiplica l'area della base pentagonale per l'altezza per trovare il volume: 105 cm2 x 10 cm.
- 105 cm2 x 10 cm = 1,050 cm3.
-
5Specifica la tua risposta in unità al cubo. La risposta finale è 1,050 cm3.Pubblicità
Consigli
- Cerca di non confondere la "base" con la "faccia di base"! La prima si riferisce a un lato (dimensione lineare) della figura bidimensionale, mentre la seconda è la base del prisma intero, di solito la parte superiore o inferiore (dimensione quadratica).
Riferimenti
- ↑ http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i22/bk7_22i6.htm
- ↑ http://www.basic-mathematics.com/volume-of-a-cube.html
- ↑ http://www.mathgoodies.com/lessons/vol1/area_trapezoid.html
- ↑ http://www.wikicalculator.com/formula_calculator/Volume-Area-of-Pentagonal-Prism-130.htm
- ↑ http://www.mathopenref.com/apothem.html
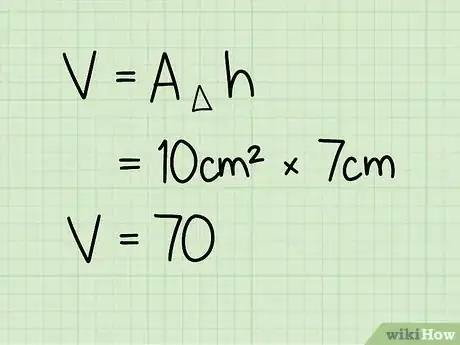

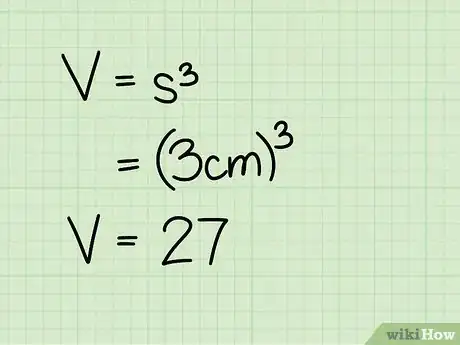



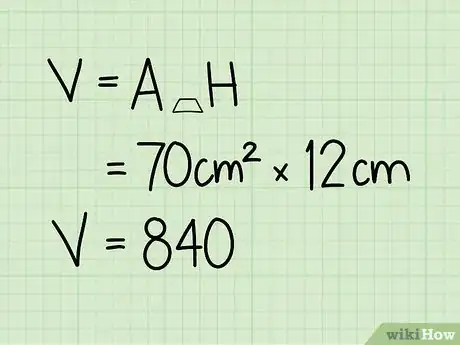
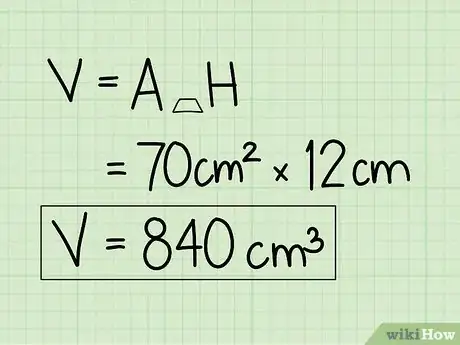
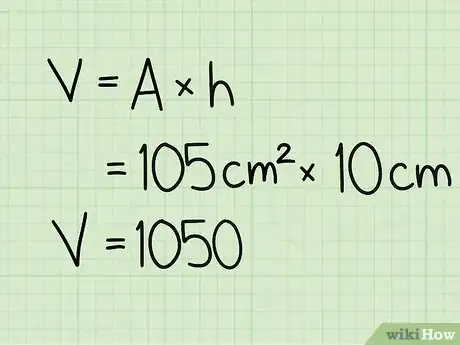
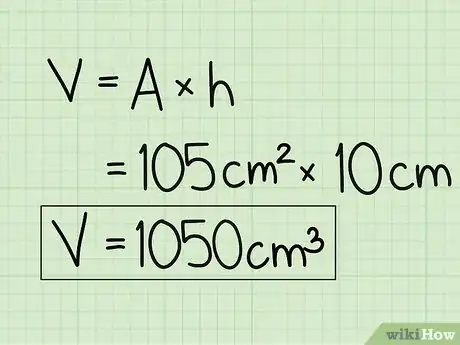


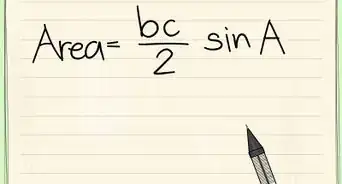
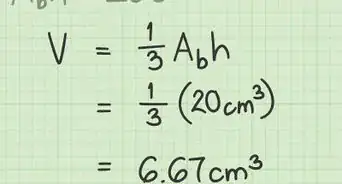




-to-Grams-(g)-Step-12-Version-4.webp)