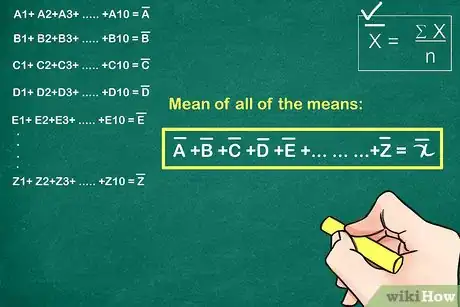Come Creare un Diagramma di Controllo

Info sull'Autore

I diagrammi di controllo sono uno strumento efficace per analizzare le prestazioni dei dati necessari per valutare un processo. Hanno molti usi. Possono essere utilizzati nell’industria per testare, ad esempio, se i macchinari stanno realizzando i prodotti entro le specifiche qualitative prestabilite. Inoltre hanno molte semplici applicazioni: i professori li utilizzano per valutare i punteggi dei test. Per creare un grafico di controllo, è utile avere Excel: ti semplificherà la vita.

Passaggi

1
Controlla che i tuoi dati soddisfino i seguenti criteri:
- I dati dovrebbero solitamente essere distribuiti normalmente intorno a una media.
  - Nell'esempio che segue, una società che produce bottiglie le riempie attorno ai 500 ml (media). In misure anglosassoni si tratta di 16 once. L’azienda sta valutando la validità del loro processo produttivo.
- Le misurazioni devono essere indipendenti l’una dall’altra.
  - Nell'esempio, le misurazioni sono suddivise in sottogruppi. I dati nei sottogruppi dovrebbero essere indipendenti dal numero di misurazioni; ogni punto di dati avrà un sottogruppo e un numero di misurazioni.
- Esempio:
2
Trova la media di ciascun sottogruppo.
- Per trovare la media, aggiungi tutte le misurazioni del sottogruppo e dividi per il numero di misurazioni in quel sottogruppo.
  - Nell'esempio, ci sono 20 sottogruppi e in ciascun sottogruppo ci sono 4 misurazioni.
- Esempio:
3
Trova la media di tutte le medie del passaggio precedente (X).
- Questo ti darà la media complessiva di tutti i punti di dati.
- La media complessiva sarà l’asse centrale del grafico (CenterLine = CL), che vale 13,75 nel nostro esempio.
4
Calcola la deviazione standard (S) dei dati (vedi Consigli).
5
Calcola il limite superiore e inferiore (UCL, LCL) utilizzando la seguente formula:
- - UCL = CL + 3 * S
  - LCL = CL – 3 * S
  - La formula rappresenta 3 deviazioni standard sopra e 3 sotto la media, rispettivamente.
6
Consulta il grafico sottostante con i passaggi dal 7 al 10.
- Esempio:
7
Disegna una linea ad ogni deviazione.
- Nell'esempio sopra, c'è una linea tracciata a uno, due e tre deviazioni standard (sigma) dalla media.
  - La zona C è a 1 sigma dalla media (verde).
  - La zona B è a 2 sigma dalla media (giallo).
  - La zona A è a 3 sigma dalla media (rosso).
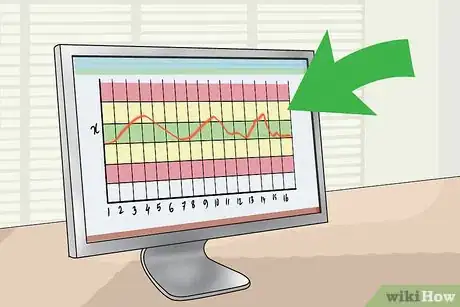
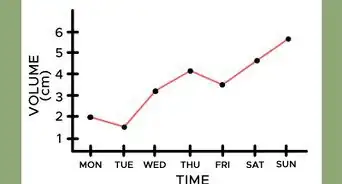
8
Disegna il grafico di controllo della media (X barrata), rappresentando graficamente il sottogruppo delle medie (asse x) rispetto al sottogruppo delle misurazioni (asse y). Il grafico dovrebbe assomigliare a qualcosa di simile:
- Esempio
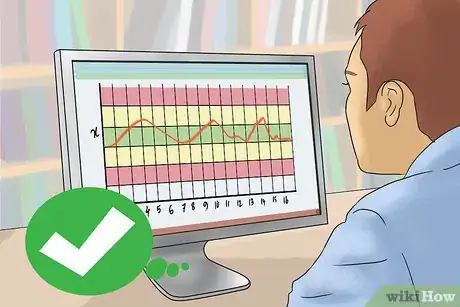
9
Valuta il grafico per vedere se il processo è fuori dal controllo, cioè oltre i valori ammissibili. Il grafico è fuori controllo se si verifica uno qualsiasi dei seguenti casi:
- Qualsiasi punto cade oltre la zona rossa (sopra o sotto la linea 3 sigma).
- 8 punti consecutivi cadono su di uno stesso lato della linea della media.
- 2 di 3 punti consecutivi rientrano nella zona A.
- 4 di 5 punti consecutivi rientrano nella zona A e/o zona B.
- 15 punti consecutivi sono all'interno della zona C.
- 8 punti consecutivi non sono in zona C.
10
Verifica se il sistema è nei limiti o fuori da ogni accettabilità.

Pubblicità

Consigli

Utilizza Excel quando crei i grafici, perché contiene delle funzioni che permettono di accelerare i calcoli.

Avvertenze

I diagrammi di controllo (generalmente) si basano su dati normalmente distribuiti. In pratica, tuttavia, sono ragionevolmente al di fuori della norma.
Per alcuni grafici, ad esempio il grafico C, può capitare che i dati siano non normalmente distribuiti.
I grafici con media mobile utilizzano regole di interpretazione diverse per soddisfare le richieste di elevata non normalità dei dati.
I grafici a media barrata tendono ad essere distribuiti normalmente anche se i dati sottostanti non lo sono.