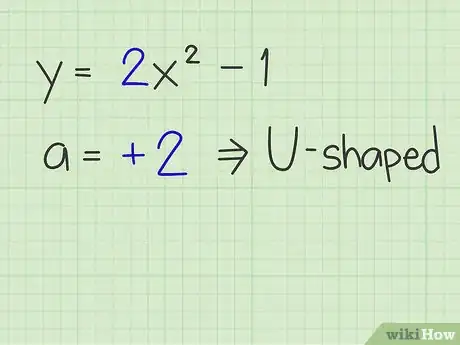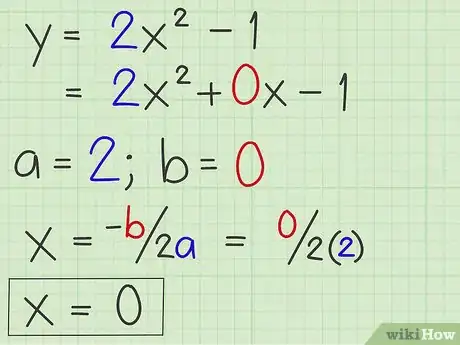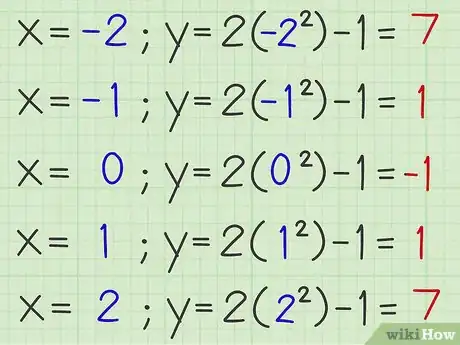Come Disegnare una Parabola

Co-redatto da Jake Adams

Una parabola è una curva bidimensionale, simmetrica rispetto a un asse e che possiede una forma arcuata. Ogni punto sulla parabola è equidistante da un punto fisso (il fuoco) e una linea retta (la direttrice). Per disegnare una parabola, devi trovare il suo vertice e molte coordinate x e y su uno dei due lati del vertice per poter disegnare il percorso da seguire. Se vuoi sapere come disegnare una parabola, comincia dal Passaggio 1.

Parte 1

Parte 1 di 2:

Disegnare una Parabola

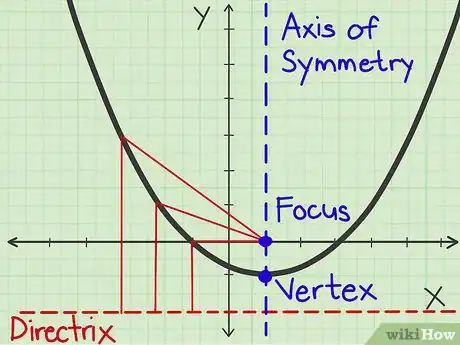
1
Distingui le parti della parabola. Potrebbero esserti state fornite delle informazioni prima di cominciare, e conoscere la terminologia ti aiuterà a evitare dei passaggi non necessari. Ecco le parti della parabola che devi conoscere:^{[1]
X
Fonte di ricerca}
- Il Fuoco. Un punto fisso all’interno della parabola che viene usato per la sua definizione formale.
- La direttrice. Una linea retta fissa. La parabola è il luogo dei punti che sono equidistanti da un punto fisso detto fuoco e dalla direttrice.
- L’asse di simmetria. L’asse di simmetria è una linea verticale che attraversa il vertice della parabola. Da ogni lato dell’asse di simmetria, la parabola risulta riflessa.
- Il vertice. Il punto in cui l’asse di simmetria attraversa la parabola è detto vertice. Se la parabola si apre verso l’alto, allora il vertice è il punto minimo; se è rivolta verso il basso, il vertice è il punto massimo.
2
Conosci l’equazione della parabola. L’equazione della parabola è y = ax²+ bx + c. Può anche essere scritta nella forma y = a(x – h)2 + k, ma, nel nostro esempio, ci soffermeremo sulla prima.
- Se a nell’equazione è positiva, allora la parabola è rivolta verso l’alto, come una "U", è ha un punto di minimo. Se a è negativo, allora è rivolta verso il basso e possiede un punto di massimo. Se hai dei problemi a ricordarti questo punto, pensala in questo modo: un’equazione con a positivo è contenta; un’equazione con a negativo è triste.^{[2]
  X
  Fonte di ricerca}
- Supponiamo che tu possieda la seguente equazione: y = 2x² -1. Questa parabola sembrerà una "U" dato che a è pari a 2, quindi positivo.
- Se la tua equazione possiede una y al quadrato anziché una x al quadrato, allora si aprirà di lato, a destra o a sinistra, come una "C" o una "C" rivolta a sinistra. Ad esempio, la parabola y² = x + 3 si apre a destra, come una "C".
3
Trova l’asse di simmetria. Ricorda che l’asse di simmetria è la retta che passa per il vertice della parabola. Corrisponde con la coordinate x del vertice, che è iI punto in cui l’asse di simmetria si incontra con la parabola. Per trovare l’asse di simmetria, usa questa formula: x = -b/2a^{[3]
X
Fonte di ricerca}
- Nell’esempio, puoi vedere che a = 2, b = 0 e c = 1. Ora, puoi calcolare l’asse di simmetria sostituendo i punti: x = -0/(2 x 2) = 0.
- Il tuo asse di simmetria è x = 0.
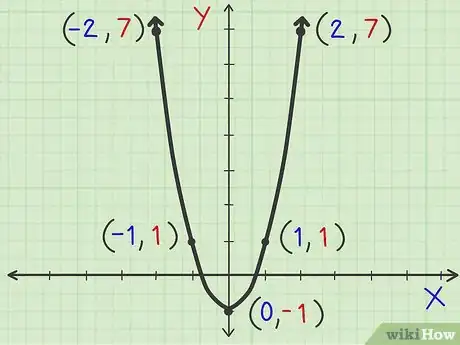
4
Trova il vertice. Una volta che hai l’asse di simmetria, puoi sostituire il valore di x per trovare la coordinata y corrispondente. Queste due coordinate individuano il vertice della parabola. In questo caso, dovresti sostituire 0 in 2x² -1 per ottenere la coordinata y. y = 2 x 0² -1 = 0 -1 = -1. Il tuo vertice è (0,-1), che è il punto in cui la parabola incontra l’asse y.^{[4]
X
Fonte di ricerca}
- I valori del vertice sono anche noti come le coordinate (h, k). Il tuo h è 0 e il tuo k è -1. Se l’equazione della parabola è scritta nella forma y = a(x – h)2 + k, allora il tuo vertice è semplicemente il punto (h, k) e non devi fare alcun calcolo matematico per trovarlo: è sufficiente interpretare il grafico in modo corretto.
5
Crea una tabella con i valori di x. In questo passo, devi creare una tabella in cui inserisci i valori di x nella prima colonna. Questa tabella conterrà le coordinate di cui avrai bisogno per disegnare la parabola.
- Il valore medio di x dovrebbe essere l’asse di simmetria.
- Dovresti includere 2 valori al di sopra e al di sotto del valore medio di x nella tabella, per ragioni di simmetria.
- Nel tuo esempio, inserisci il valore dell’asse di simmetria, x = 0, al centro della tabella.
6
Calcola i valori delle coordinate y. Sostituisci ogni valore di x nell’equazione della parabola e calcola i valori della y. Inserisci i valori calcolati di y nella tabella. Nel tuo esempio, l’equazione della parabola è calcolata come segue:
- Per x = -2, y è calcolato come: y = 2 x (-2)² - 1 = 8 - 1 = 7
- Per x = -1, y è calcolato come: y = 2 x (-1)² - 1 = 2 - 1 = 1
- Per x = 0, y è calcolato come: y = 2 x (0)² - 1 = 0 - 1 = -1
- Per x = 1, y è calcolato come: y = 2 x (1)² - 1 = 2 - 1 = 1
- Per x = 2, y è calcolato come: y = 2 x (2)² - 1 = 8 - 1 = 7
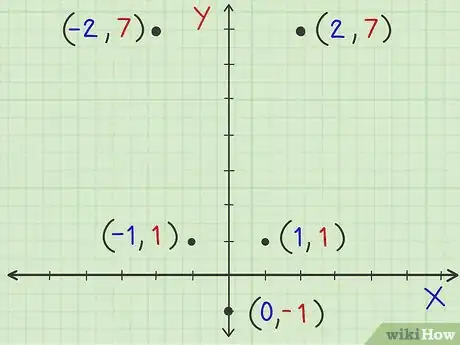
7
Inserisci i valori di y calcolati nella tabella. Ora che hai trovato almeno 5 coppie di coordinate della parabola, sei praticamente pronto per disegnarla. Basandoti sul tuo lavoro, ora possiedi i seguenti punti: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Ora, puoi tornare all’idea che la parabola si riflette rispetto al suo asse di simmetria. Questo significa che le coordinate y dei punti che sono gli uni i riflessi degli altri, sarà la stessa. Le coordinate y per le coordinate x pari a -2 e 2 sono entrambe 7, le coordinate y per le coordinate x pari a -1 e 1 sono entrambe 1, e così via.
8
Disegna i punti della tabella sul grafico. Ogni riga della tabella forma dei punti (x, y) sul piano delle coordinate. Disegna tutti i punti presenti nella tabella sul piano delle coordinate.
- L’asse delle x va da sinistra a destra; l’asse y dal basso verso l’alto.
- I numeri positivi della y si trovano sopra il punto (0, 0) e i numeri negativi dell’asse y si trovano sotto il punto (0, 0).
- I numeri positivi dell’asse x si trovano a destra di (0, 0) e quelli negativi a sinistra del punto (0, 0).
9
Collega i punti. Per disegnare la parabola, collega i punti trovati al passo precedente. Il grafico del tuo esempio sembrerà una U. Assicurati di collegare i punti usando una linea curva, invece di collegarli con dei segmenti retti. Questo permetterà di rappresentare accuratamente l’aspetto della parabola. Puoi anche disegnare delle frecce che puntino verso l’alto o verso il basso agli estremi della parabola, a seconda di quale sia la direzione verso cui è rivolta. Questo indica che il grafico della parabola continuerà al di fuori del grafico.^{[5]
X
Fonte di ricerca}

Pubblicità

Parte 2

Parte 2 di 2:

Spostare il Grafico della Parabola

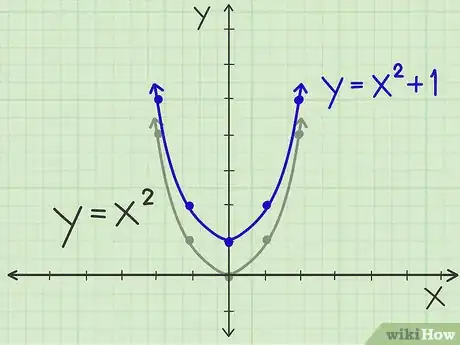
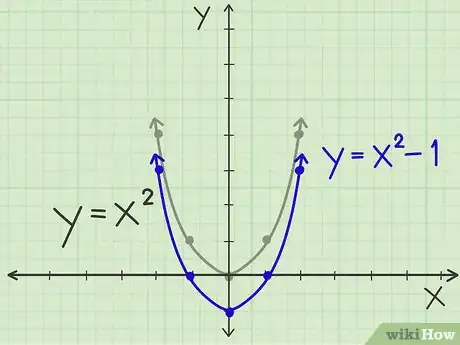
Se vuoi sapere una scorciatoia per spostare la parabola senza dover calcolare il vertice e diversi punti su di essa, allora devi capire come leggere l’equazione di una parabola e spostarla in alto, in basso, a destra o a sinistra. Inizia con la parabola di base: y = x². Questa ha un vertice (0, 0) ed è rivolta verso l’alto. Alcuni punti su di essa sono ad esempio (-1, 1), (1, 1), (-2, 4), (2, 4), e così via. Puoi capire come spostare la parabola a seconda dell’equazione che possiedi. ^{[6]
X
Fonte di ricerca}

1
Sposta il grafico della parabola verso l’alto. Prendi l’equazione y = x² +1. Tutto ciò che devi fare è spostare la parabola originaria in alto di una unità, quindi il vertice ora è (0, 1) invece di (0, 0). Avrà sempre esattamente la stessa forma della parabola originaria, ma ogni coordinata y si troverà più in alto di un’unità. Quindi, invece di (-1, 1) e (1, 1), avresti (-1, 2) e (1, 2), e così via.
2
Sposta il grafico della parabola verso il basso. Prendi l’equazione y = x² -1. Tutto ciò che devi fare è spostare la parabola originaria in basso di una unità, in modo che il vertice ora sia (0, -1) invece di (0, 0). Avrà sempre esattamente la stessa forma della parabola originaria, ma ogni coordinata y si troverà più in basso di un’unità. Quindi, invece di (-1, 1) e (1, 1), avresti (-1, 0) e (1, 0), e così via.
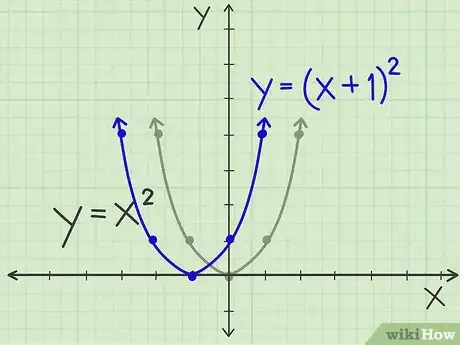
3
Sposta il grafico della parabola verso sinistra. Prendi l’equazione y = (x + 1)². Tutto ciò che devi fare è spostare la parabola originaria a sinistra di una unità, in modo che il vertice ora sia (-1, 0) invece di (0, 0). Avrà sempre esattamente la stessa forma della parabola originaria, ma ogni coordinata x si troverà più a sinistra di un’unità. Quindi, invece di (-1, 1) e (1, 1), avresti (-2, 1) e (0, 1), e così via.
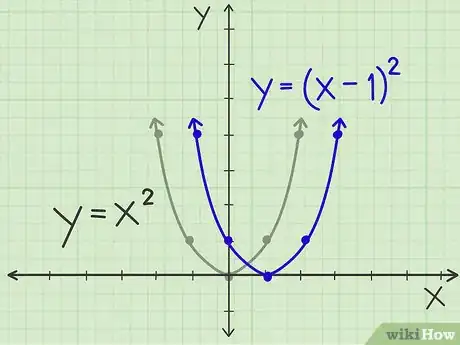
4
Sposta il grafico della parabola verso destra. Prendi l’equazione y = (x - 1)². Tutto ciò che devi fare è spostare la parabola originaria a destra di una unità, in modo che il vertice ora sia (1, 0) invece di (0, 0). Avrà sempre esattamente la stessa forma della parabola originaria, ma ogni coordinata x si troverà più a destra di un’unità. Quindi, invece di (-1, 1) e (1, 1), avresti (0, 1) e (2, 1), e così via.

Pubblicità