Come Leggere i Numeri In Sistema Binario

Info sull'Autore

Riuscire a comprendere cosa vogliano dire quelle righe di 1 e 0 può sembrare un'impresa assai ardua. Tuttavia, con un po' di logica è facile capirne il significato. L'uomo si è abituato ad usare il sistema decimale semplicemente perché abbiamo 10 dita. I computer, invece, possiedono solo due "dita" - acceso o spento, o "1" e "0" - ed è per questo che è stato creato il sistema binario.

Metodo 1

Metodo 1 di 3:

Metodo 1: Esponenti

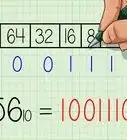
1
Scrivi il numero binario che vuoi convertire. In questo esempio, useremo il numero 101010.
2
Moltiplica ogni cifra del numero binario per la potenza di 2 corrispondente al suo valore posizionale. Ricorda, il codice binario si legge da destra verso sinistra e la posizione più destra è la posizione 0.
3
Somma insieme tutti i risultati. Procediamo da destra verso sinistra.
- 0 × 2⁰ = 0
- 1 × 2¹ = 2
- 0 × 2² = 0
- 1 × 2³ = 8
- 0 × 2⁴ = 0
- 1 × 2⁵ = 32
- Totale = 42
Pubblicità

Metodo 2

Metodo 2 di 3:

Metodo 2: Esponenti in Formato Alternativo

1
Scrivi il numero binario. Usiamo il numero 101. Il procedimento è lo stesso del metodo 1, ma segue un formato leggeremente differente e più semplice da capire.
- 101= (1*2) elevato alla 2 + (0*2) elevato alla 1 + (1*2) elevato alla 0
- 101= (2*2) + (0*0) + (1)
- 101= 4 + 0 + 1
- 101= 5
  - Lo zero non è un numero, ma bisogna tenere conto del suo valore posizionale.

Metodo 3

Metodo 3 di 3:

Metodo 3: Valore Posizionale

1
Scrivi il tuo numero binario. In questo esempio, useremo il numero 00101010.
2
Leggi il numero da destra verso sinistra. Ogni volta che si passa ad una posizione successiva, il valore di quella posizione è uguale al valore di quella precedente moltiplicato per 2. La prima cifra da destra ha valore posizionale 1, la seconda ha valore 2, la terza 4 e così via.
3
Considera solo i valori posizionali associati ad una posizione in cui è scritto un 1 e sommali. Le posizioni con gli 0 vanno contate quando si assegna il valore posizionale, ma non vanno considerate nella somma.
- Seguendo i passaggi, in questo esempio si ottengono 2, 8, e 32, che sommati danno come risultato 42.
  - Puoi leggere il numero come un 'no' per 1, 'sì' per 2, 'no' per 4, 'sì' per 8, 'no' per 16, 'sì' per 32, 'no' per 64 e 'no' per 128. "Sì" significa che il valore va contato nella somma, "no" significa che va saltato. Puoi fermarti all'ultimo 1 del numero, se tutte le cifre rimanenti sono 0.
4
Traduci il valore ottenuto in lettere o segni di interpunzione (codice ASCII). Puoi anche convertire i numeri binari in numeri decimali o convertire i numeri decimali in numeri binari.
- Nei segni di interpunzione, al valore 42 corrisponde l'asterisco (*). Clicca qui per consultare una tabella di conversione.
Pubblicità

Consigli

Anche i numeri decimali, che sono quelli con cui abbiamo a che fare ogni giorno, hanno valori posizionali. Assumendo che si stia lavorando con numeri interi, la cifra più a destra è la cifra delle unità, la seconda più a destra è quella delle decine, la terza quella delle centinaia e così via. I valori posizionali del sistema binario sono, partendo da destra, 1, 2, 4, 8 e così via.
Nel sistema binario si conta come nel sistema decimale: si aumenta di una unità la cifra più a destra finché questa non può più aumentare (nel decimale da 8 a 9, nel binario da 0 a 1), poi si riporta il valore incrementando di 1 la cifra a sinistra successiva e si ricomincia con quella più a destra, partendo da 0.