wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 122 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 93 722 volte
Il sistema numerico binario (o base due) possiede due possibili valori (0 e 1) per ogni posizione del sistema. Per contrasto, il sistema numerico decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) per ogni posizione del sistema.
Per evitare di fare confusione quando si usano diversi sistemi numerici, è possibile esplicitare la base di ogni numero scrivendola come pedice del numero stesso. Ad esempio, si può specificare che il numero binario 10011100 è in "base due" scrivendolo come 100111002. il numero decimale 156 può essere scritto come 15610 e letto come "centocinquantasei, base dieci".
Poiché il sistema binario è il linguaggio interno utilizzato dai computer elettronici, tutti i programmatori seri dovrebbero sapere come convertire dal sistema binario a quello decimale. Il processo inverso, ovvero la conversione dal sistema decimale a quello binario, è spesso più difficile da imparare per primo.
Passaggi
Metodo della Notazione Posizionale
-
1Per questo esempio, convertiremo il numero binario 100110112 in decimale. Scrivi le potenze di due, andando da destra verso sinistra. Comincia da 20, che vale 1. Aumenta l'esponente di una unità per ogni potenza successiva. Fermati quando il numero di elementi nell'elenco è pari al numero di cifre del numero binario. Il numero dell'esempio, 10011011, ha otto cifre, per cui l'elenco delle potenze, di otto elementi, risulterebbe questo: 128, 64, 32, 16, 8, 4, 2, 1
-
2Trascrivi le cifre del numero binario sotto le loro corrispondenti potenze di due. Ora scrivi 10011011 sotto i numeri 128, 64, 32, 16, 8, 4, 2 e 1 in modo che ogni cifra binaria corrisponda alla sua potenza di due. L’uno alla destra del numero binario dovrebbe corrispondere all’uno sulla destra delle elencate potenze di due e così via. Puoi anche scrivere le cifre binarie sopra le potenze di due, se preferisci. L’importante è che corrispondano.
-
3Collega le cifre del numero binario con le loro corrispondenti potenze di due. Traccia delle linee, partendo da destra, in modo che colleghino ogni cifra consecutiva del numero binario alla potenza di due presente nella lista sovrastante. Inizia tracciando una linea della prima cifra del numero binario alla prima potenza di due della riga precedente. Poi tira una linea dalla seconda cifra del numero binario alla seconda potenza di due presente nella lista. Continua a collegare ogni cifra con la corrispondente potenza di due. Questo ti aiuterà a visualizzare la relazione tra i due insieme di numeri.
-
4Se la cifra è un 1, allora scrivi la potenza di due corrispondente al di sotto di una linea tracciata sotto il numero binario. Se la cifra è uno 0, scrivi uno 0 al di sotto della linea e della cifra.
- Visto che "1" corrisponde a "1", diventa un "1". Siccome "2" corrisponde a "1", diventa un "2". Siccome "4" corrisponde a "0", diventa "0". Siccome "8" corrisponde a "1", diventa "8" e, poiché "16" corrisponde a "1", diventa "16". "32" corrisponde a "0" e fa "0" e "64", visto che corrisponde a "0", diventa "0", mentre "128", corrispondendo a "1", diventa "128".
-
5Somma i valori finali. A questo punto, somma i numeri scritti sotto la riga. Fai così: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. Questo è il numero decimale equivalente al numero binario 10011011.
-
6Scrivi la risposta aggiungendo la sua base in pedice. A questo punto tutto ciò che devi fare è scrivere 15510 per specificare che stai lavorando con un numero decimale sotto forma di potenze di 10. Più ti abituerai a convertire un numero da binario a decimale, più ti risulterà semplice memorizzare le potenze di due, riuscendo così a raggiungere l’obiettivo più velocemente.
-
7Usa questo metodo per convertire sotto forma di decimale un numero binario con la virgola decimale. Puoi usare questo metodo anche quando vuoi convertire un numero binario come 1,12 in decimale. Tutto ciò che devi fare è sapere che il numero posto sulla sinistra rispetto alla virgola è nella posizione delle unità, com’è normale, mentre il numero a destra della virgola è nella posizione delle "metà" o 1 x (1/2).
- L’"1" a sinistra della virgola è uguale a 20, cioè 1. L’"1" sulla destra corrisponde a 2-1, cioè 0,5. Somma 1 con 0,5, ottenendo 1,5, che, in notazione decimale, corrisponde a 1,12 .
Pubblicità
Metodo del Raddoppio
-
1Trascrivi il numero binario. Questo metodo non utilizza le potenze. Per questo motivo, è un metodo più comodo da usare per convertire a mente numeri grandi, poiché devi ricordare un solo risultato parziale alla volta. La prima cosa che devi fare è trascrivere il numero che vuoi convertire usando il metodo del raddoppio. Supponiamo che tu voglia lavorare con 10110012. Scrivilo.
-
2Iniziando da sinistra, raddoppia il totale precedente e aggiungi la cifra corrente. Siccome stai lavorando con il numero 10110012, la tua prima cifra sulla sinistra è 1. Il totale precedente è 0 siccome non hai ancora iniziato. Devi raddoppiare questo totale, 0, dopodiché aggiungere 1, la cifra corrente. 0 x 2 + 1 = 1, così il tuo nuovo totale parziale diventa 1.
-
3Raddoppia questo parziale e aggiungi la seguente cifra a sinistra. Il tuo totale adesso è 1 e la nuova cifra da prendere in considerazione è 0. A questo punto, raddoppia 1 e aggiungi 0. 1 x 2 + 0 = 2. Il tuo nuovo totale diventa 2.
-
4Ripeti il passaggio precedente. Continua. Raddoppia il totale parziale e aggiungi 1, la cifra seguente. 2 x 2 + 1 = 5. Il tuo nuovo totale adesso è 5.
-
5Continua raddoppiando il totale parziale, 5, e aggiungi la cifra che segue, 1. 5 x 2 + 1 = 11. Il tuo nuovo totale è 11.
-
6Ripeti ancora il procedimento. Raddoppia il tuo totale attuale, 11, e aggiungi la cifra che segue, 0. 2 x 11 + 0 = 22.
-
7Ripeti ancora il tutto. Adesso raddoppia il totale corrente, 22, e aggiungi 0, la cifra che segue. 22 × 2 + 0 = 44.
-
8Continua a raddoppiare il totale parziale e ad aggiungere la cifra che segue finché non avrai preso in considerazione tutte le cifre. Con l’ultimo numero hai quasi finito! Tutto ciò che devi fare è prendere il totale, 44, raddoppiarlo e aggiungere 1, l’ultima cifra. 2 × 44 + 1 = 89. Hai finito! Sei riuscito a convertire 100110112 sotto forma di notazione decimale, 89.
-
9Trascrivi la risposta specificando la base in pedice. Il risultato è 8910 per evidenziare che stai lavorando con un numero decimale, che è a base 10.
-
10Usa questo metodo per convertire qualunque base in decimale. Il raddoppio è usato perché il numero dato è in base 2. Se il numero dato fosse espresso con una base differente, bisognerebbe sostituire il 2 con la base del numero dato. Ad esempio, se il numero da convertire fosse in base 37, basterebbe scambiare il *2 con un *37. Il risultato finale sarà sempre un numero decimale (base 10)Pubblicità
Consigli
- Fai pratica. Prova a convertire i numeri binari 110100012, 110012 e 111100012. Gli equivalenti in base decimale sono, rispettivamente, 20910, 2510 e 24110.
- La calcolatrice fornita dal tuo sistema operativo è in grado di fare questa conversione al posto tuo, ma se sei un programmatore è meglio che tu abbia una buona conoscenza del processo di conversione. È possibile accedere alle opzioni di conversione della calcolatrice cliccando sul pulsante Visualizza e selezionando Programmatore o Scientifica. Su Linux, è possibile utilizzare galculator.
- Nota: questo articolo spiega solo come passare da un sistema numerico all'altro e non tratta della traduzione in codice ASCII.
Avvertenze
- Questo metodo utilizza numeri binari senza virgola, non numeri in virgola mobile o virgola fissa.





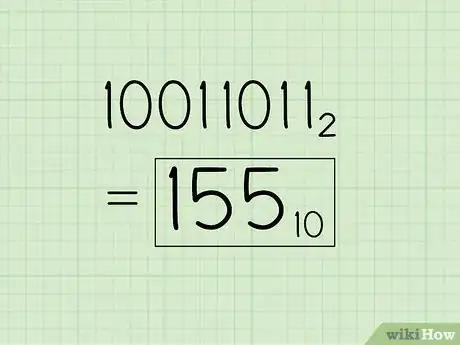
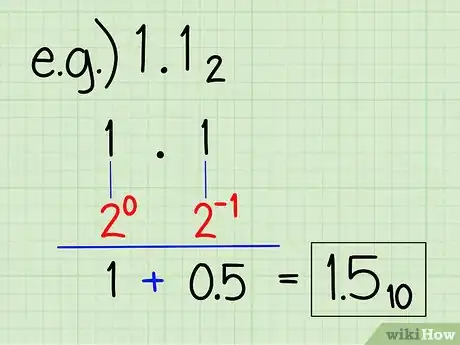









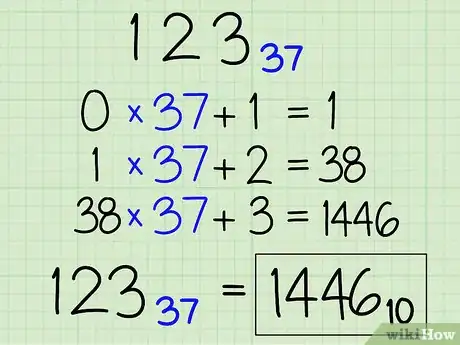



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
