Questo articolo è stato co-redatto da Grace Imson, MA. Grace Imson è un'insegnante di matematica con oltre 40 anni di esperienza. Grace è attualmente docente di matematica presso il City College of San Francisco e ha lavorato in precedenza nel Dipartimento di Matematica della Saint Louis University. Oltre all'università, ha insegnato matematica alle scuole elementari, medie e superiori. Ha conseguito la Laurea Magistrale in Educazione, con specializzazione in Amministrazione e Supervisione, presso la Saint Louis University.
Questo articolo è stato visualizzato 420 003 volte
Non c’è esame di matematica che non preveda il calcolo dell’ipotenusa di almeno un triangolo rettangolo; tuttavia, non devi preoccuparti perché si tratta di un calcolo semplice! Tutti i triangoli rettangoli hanno un angolo retto (a 90°) e il lato opposto a quest’angolo si chiama ipotenusa. Il filosofo e matematico greco Pitagora, 2500 anni fa, ha trovato un metodo semplice per calcolare la lunghezza di questo lato, che si usa ancora ai giorni nostri. Questo articolo ti insegnerà a utilizzare il ‘Teorema di Pitagora’ quando conosci la lunghezza dei due cateti e sfruttare il ‘Teorema dei Seni’ quando conosci solo la lunghezza di un lato e l’ampiezza di un angolo (oltre a quello retto). Infine ti verrà proposto come riconoscere e memorizzare il valore dell’ipotenusa in triangoli rettangoli speciali che spesso fanno la loro comparsa nei test di matematica.
Passaggi
Teorema di Pitagora
-
1Impara il ‘Teorema di Pitagora’. Questa legge descrive la relazione che intercorre fra i lati di un triangolo rettangolo ed è una delle più utilizzate in matematica (anche nei compiti in classe!). Il teorema enuncia che in ogni triangolo rettangolo la cui ipotenusa è ‘c’ e i cateti sono ‘a’ e ‘b’ vale la relazione : a2 + b2 = c2.
-
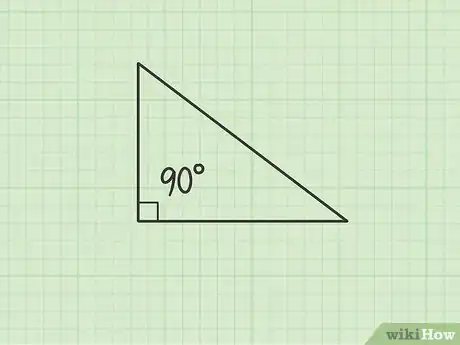
2Accertati che il triangolo sia rettangolo. Infatti il Teorema di Pitagora è valido solo per questo tipo di triangolo, dato che per definizione è l’unico a possedere un’ipotenusa. Se il triangolo in oggetto ha un angolo che misura esattamente 90°, allora sei di fronte a un triangolo rettangolo e puoi procedere con i calcoli.
- Gli angoli retti vengono spesso identificati, sia sui libri di testo che nei compiti in classe, con un piccolo quadretto. Questo segno speciale significa "90°".
-
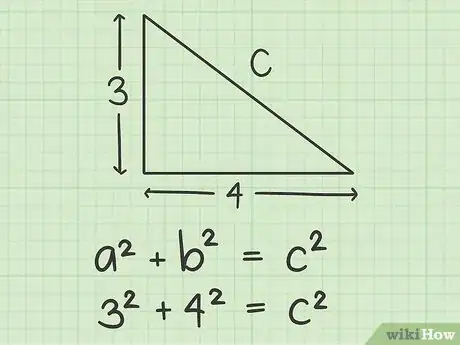
3Assegna le variabili a, b e c ai lati del triangolo. La variabile "c" si assegna sempre all’ipotenusa, il lato più lungo. I cateti saranno a e b (non importa in quale ordine, il risultato non cambia). A questo punto inserisci nella forma del Teorema di Pitagora i valori corrispondenti alle variabili. Per esempio:
- Se i cateti del triangolo misurano 3 e 4, allora assegna alle lettere questi valori: a = 3 e b = 4; l’equazione può essere riscritta come: 32 + 42 = c2.
-
4Trova i quadrati di a e b. Per farlo moltiplica semplicemente ogni valore per se stesso, quindi: a2 = a x a. Trova i quadrati di a e b e inserisci i risultati nella formula.
- Se a = 3, a2 = 3 x 3 = 9. Se b = 4, b2 = 4 x 4 = 16.
- Una volta inseriti questi numeri nella formula, l’equazione dovrebbe apparire così: 9 + 16 = c2.
-
5Somma fra loro i valori di a2 e b2. Inserisci il risultato nella formula e avrai il valore di c2. Manca solo un ultimo passaggio e avrai risolto il problema.
- Nel nostro esempio otterrai 9 + 16 = 25, quindi puoi affermare che 25 = c2.
-
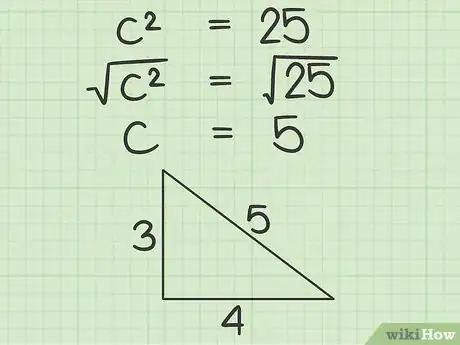
6Estrai la radice quadrata di c2. Puoi usare la funzione della tua calcolatrice (oppure la tua memoria o le tavole di moltiplicazione) per trovare la radice quadrata di c2. Il risultato corrisponde alla lunghezza dell’ipotenusa.
- Per terminare i calcoli del nostro esempio: c2 = 25. La radice quadrata di 25 è 5 (5 x 5 = 25, quindi Sqrt(25) = 5). Ciò significa che c = 5, la lunghezza dell’ipotenusa!
Pubblicità
Triangoli Rettangoli Speciali
-
1Impara a riconoscere le Terne Pitagoriche. Queste sono composte da tre numeri interi (associati ai lati dei triangoli rettangoli) che soddisfano il Teorema di Pitagora. Si tratta di triangoli che vengono usati molto spesso nei libri di testo di geometria e nei compiti in classe. Se memorizzi, in particolare, le prime due Terne Pitagoriche, risparmierai un sacco di tempo durante gli esami perché conoscerai immediatamente il valore dell’ipotenusa!
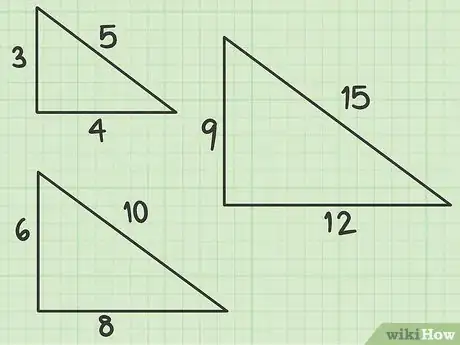
- La prima Terna Pitagorica è: 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Se ti viene proposto un triangolo rettangolo i cui cateti sono 3 e 4, puoi essere sicuro che l’ipotenusa è pari a 5 senza dover fare alcun calcolo.
- La Terna Pitagorica è valida anche per i multipli di 3-4-5, purché si mantengano le proporzioni fra i vari lati. Ad esempio, un triangolo rettangolo di lato 6 e 8 avrà l’ipotenusa pari a 10 (62 + 82 = 102, 36 + 64 = 100). Lo stesso vale per 9-12-15 e anche per 1,5-2-2,5. Prova a verificarlo da solo con i calcoli matematici.
- La seconda Terna Pitagorica molto diffusa negli esami di matematica è 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Anche in questo caso sono validi i multipli che rispettano le proporzioni, ad esempio: 10-24-26 e 2,5-6-6,5.
-
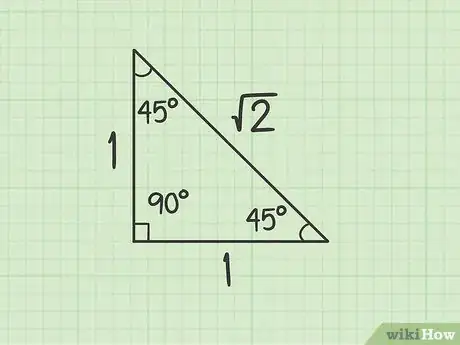
2Memorizza i rapporti fra i lati di un triangolo con angoli 45-45-90. In questo caso siamo di fronte a un triangolo rettangolo isoscele, che viene spesso usato nei compiti in classe, e i problemi a esso correlati sono semplici da risolvere. Il rapporto fra i lati, in questo caso specifico, è 1:1:Sqrt(2) il che significa che i cateti sono fra loro uguali e che l’ipotenusa è pari alla lunghezza del cateto moltiplicata per la radice di due.
- Per calcolare l’ipotenusa di un triangolo rettangolo isoscele di cui conosci la lunghezza di un cateto, basta moltiplicare quest’ultimo per il valore di Sqrt(2).
- Sapere i rapporti fra i lati è molto utile quando il problema ti fornisce i valori dei lati espressi come variabili e non come numeri interi.
-
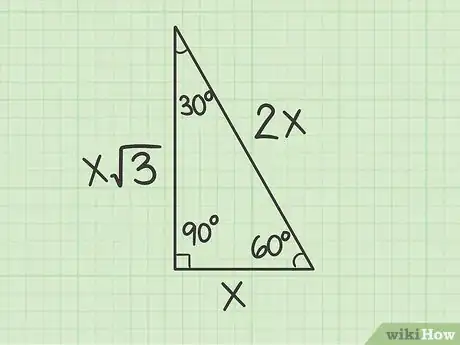
3Impara la relazione fra i lati di un triangolo con angoli 30-60-90. In questo caso hai un triangolo rettangolo con angoli di 30°, 60° e 90° che corrisponde alla metà di un triangolo equilatero. I lati di tale triangolo hanno una rapporto pari a: 1:Sqrt(3):2 oppure: x:Sqrt(3)x:2x. Se conosci la lunghezza di un cateto e devi trovare l’ipotenusa, il procedimento è molto semplice:
- Se conosci il valore del cateto minore (quello opposto all’angolo di 30°) moltiplicane semplicemente la lunghezza per due e trovi il valore dell’ipotenusa. Ad esempio se il cateto minore è pari a 4, l’ipotenusa è uguale a 8.
- Se conosci il valore del cateto maggiore (quello opposto all’angolo di 60°) allora moltiplicane la lunghezza per 2/Sqrt(3) e otterrai il valore dell’ipotenusa. Ad esempio se il cateto maggiore è 4, l’ipotenusa deve essere 4,62.
Pubblicità
Teorema dei Seni
-
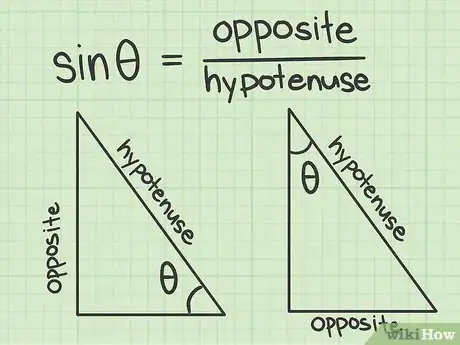
1Comprendi cos’è il "seno". I termini "seno," "coseno" e "tangente" fanno tutti riferimento a vari rapporti fra gli angoli e/o i lati di un triangolo rettangolo. In un triangolo rettangolo il seno di un angolo è definito come la lunghezza del lato opposto all’angolo diviso per la lunghezza dell’ipotenusa del triangolo. Nelle calcolatrici e nelle equazioni questa funzione viene abbreviata con il simbolo: sin.
-
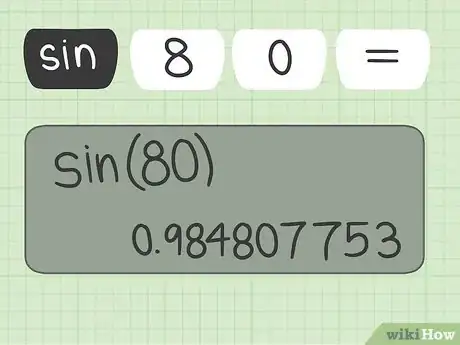
2Impara a calcolare il seno. Anche le calcolatrici scientifiche più semplici hanno la funzione di calcolo del seno. Controlla il tasto indicato con il simbolo sin. Per trovare il seno di un angolo, devi premere il tasto sin e poi digitare il valore dell’angolo espresso in gradi. In alcuni modelli di calcolatrici, devi fare esattamente l’opposto. Fai qualche prova o controlla il manuale della tua calcolatrice per capire come funziona.
- Per trovare il seno di un angolo di 80°, devi digitare sin 80 e premere il tasto di invio o di uguale oppure devi digitare 80 sin. (Il risultato è -0,9939.)
- Puoi anche fare una ricerca online con le parole "calcolatore del seno", troverai molte calcolatrici virtuali che faranno luce su molti dubbi.
-
3Impara il ‘Teorema dei Seni’. Si tratta di uno strumento molto utile per risolvere i problemi legati ai triangoli rettangoli. In particolare ti permette di trovare il valore dell’ipotenusa quando conosci la lunghezza di un lato e il valore di un altro angolo oltre a quello retto. In ogni triangolo rettangolo i cui lati siano a, b e c con angoli A, B e C il Teorema dei Seni afferma che: a / sin A = b / sin B = c / sin C.
- Il Teorema dei Seni può essere applicato per risolvere problemi di ogni triangolo, ma solo quelli rettangoli hanno l’ipotenusa.
-
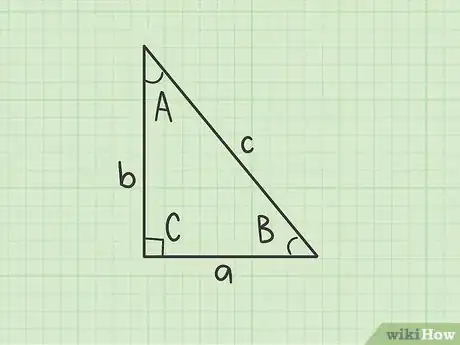
4Assegna le variabili a, b e c ai lati del triangolo. L’ipotenusa deve essere "c". Per semplicità chiamiamo il lato noto "a" e l’altro "b". Ora assegna le variabili A, B e C agli angoli. Quello opposto all’ipotenusa deve chiamarsi "C". Quello opposto al lato "a" è l’angolo "A" e quello opposto al lato "b" si chiama "B".
-
5Calcola il valore del terzo angolo. Dato che uno è retto, sai che C = 90° puoi facilmente calcolare i valori di A o B. La somma degli angoli interni di un triangolo è sempre 180° quindi puoi impostare l’equazione: 180 – (90 + A) = B che può anche essere scritta come: 180 – (90 + B) = A.
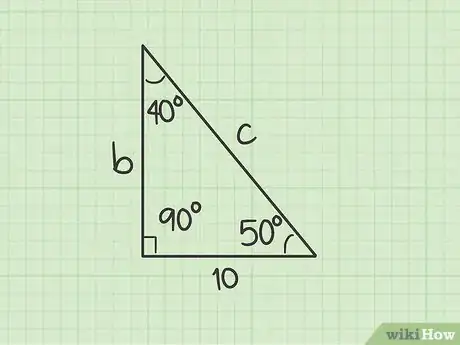
- Ad esempio, se sai che A = 40°, allora B = 180 – (90 + 40). Svolgendo i calcoli: B = 180 – 130 ottieni che: B = 50°.
-
6Esamina il triangolo. A questo punto dovresti conoscere il valore dei tre angoli e la lunghezza del lato a. Ora devi inserire queste informazioni nella formula del Teorema dei Seni per determinare la lunghezza degli altri due lati.
- Per continuare con il nostro esempio, consideriamo che a = 10. L’angolo C = 90°, l’angolo A = 40° e l’angolo B = 50°.
-
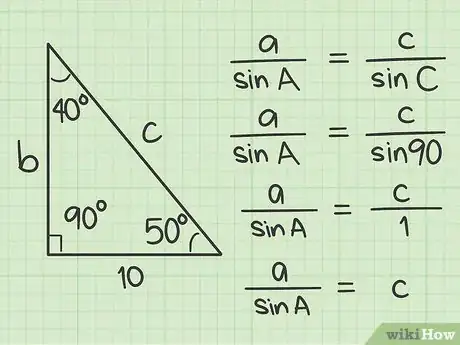
7Applica il Teorema dei Seni al triangolo. Devi inserire i valori noti nella formula e risolverla per c (la lunghezza dell’ipotenusa): a / sin A = c / sin C. La formula può sembrare complicata ma il seno di 90° è una costante ed è sempre uguale a 1! Ora semplifica l’equazione: a / sin A = c / 1 oppure: a / sin A = c.
-
8Dividi la lunghezza del lato a per il seno dell’angolo A per trovare il valore dell’ipotenusa! Puoi farlo in due passaggi differenti, prima calcolando il seno di A e annotando il risultato e poi dividendo quest’ultimo per a. In alternativa inserisci tutti i valori nella calcolatrice. Se preferisci questo secondo metodo, non dimenticare di digitare le parentesi dopo il segno di divisione. Ad esempio digita: 10 / (sin 40) oppure 10 / (40 sin), in base al modello di calcolatrice.
- Nel nostro esempio troverai che sin 40 = 0,64278761. A questo punto per trovare c, dividi la lunghezza di a per questo numero: 10 / 0,64278761 = 15,6, questo è il valore della lunghezza dell’ipotenusa!
Pubblicità
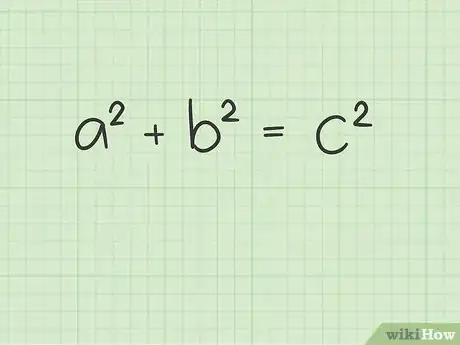
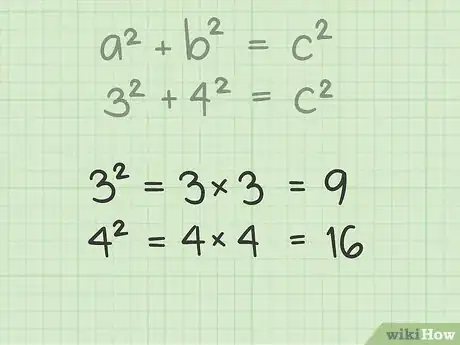
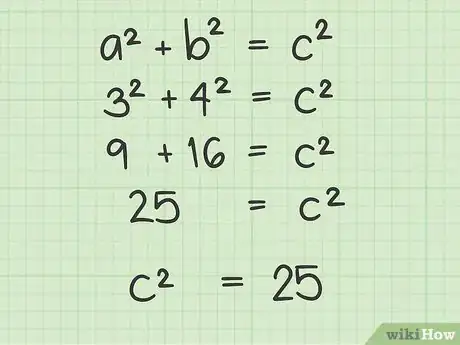
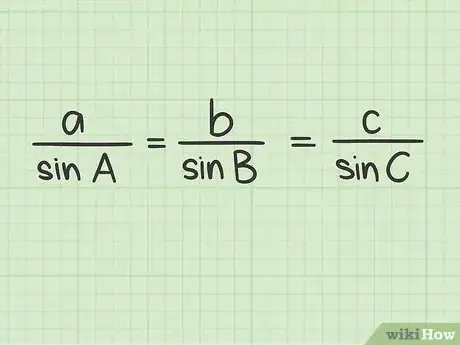

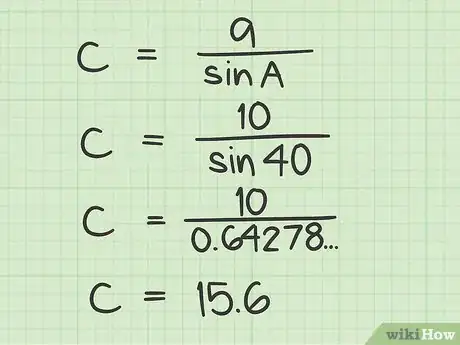




-to-Grams-(g)-Step-12-Version-4.webp)