wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 24 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 15 956 volte
Un'equazione quadratica è un'equazione matematica in cui la potenza più alta di x (grado dell'equazione) è due. Ecco un esempio di tale equazione: 4x2 + 5x + 3 = x2 - 5. Risolvere questo tipo di equazione è complicato, poiché i metodi usati per x2 non funzionano per x, e vice versa. Scomporre in fattori il termine quadratico o l’uso della formula quadratica sono due metodi che aiutano a risolvere un’equazione di secondo grado.
Passaggi
Uso della scomposizione in fattori
-
1Scrivi tutti i termini su un lato, preferibilmente sul lato dove x2 è positivo.
-
2Scomponi l'espressione in fattori.
-
3In equazioni separate, uguaglia ciascun fattore a zero .
-
4Risolvi ciascuna equazione indipendentemente. Sarebbe meglio non scrivere le frazioni improprie come numeri misti, anche se sarebbe corretto da un punto di vista matematico.Pubblicità
Uso della formula quadratica
Scrivi tutti i termini su un lato, preferibilmente sul lato dove x2 è positivo. Trova i valori di a, b e c. a è il coefficiente di x2, b è il coefficiente di x e c la costante (non ha una x). Ricordati di scrivere anche il segno del coefficiente.
-
1Calcola il prodotto di 4, a e c. Capirai la ragione di questo passaggio più avanti.
-
2Scrivi la formula quadratica, che è:
-
3Sostituisci i valori di a, b, c, e 4ac nella formula:
-
4Aggiusta i segni del numeratore, finisci di moltiplicare il denominatore e calcola b2. Nota che anche quando b è negativo, b2 è positivo.
-
5Finisci la parte sotto la radice quadrata. Questa parte della formula si chiama "discriminante". A volte è meglio calcolarlo per primo, poiché ti può dire in anticipo il tipo di risultato che darà la formula.
-
6Semplifica la radice quadrata. Se il numero sotto la radice è un quadrato perfetto, otterrai un numero intero. Altrimenti, semplifica fino alla versione quadratica più semplice. Se il numero è negativo, e tu sei sicuro che dovrebbe essere negativo, allora la radice sarà complessa.
-
7Separa i più o meno in opzione più o opzione meno. (Questo passaggio vale solo se la radice quadrata è stata semplificata.)
-
8Calcola la possibilità più o quella meno in modo separato...
-
9...e riducila ciascuna ai minimi termini. Le frazioni improprie non devono essere scritte come numeri misti, ma se vuoi puoi farlo.Pubblicità
Completare il quadrato
Questo metodo potrebbe essere più facile da applicare con un tipo di equazione quadratica differente.
Es: 2x2 - 12x - 9 = 0
-
1Scrivi tutti i termini su un lato, preferibilmente sul lato dove a o x2 siano positivi.2x2 - 9 = 12x2x2 - 12x - 9 = 0
-
2Sposta c, o constante, sull'altro lato.2x2 - 12x = 9
-
3Se necessario, dividi entrambi i lati per il coefficiente di a o x2.x2 - 6x = 9/2
-
4Dividi b per due ed eleva al quadrato. Aggiungi su entrambi i lati.-6/2 = -3(-3)2 = 9x2 - 6x + 9 = 9/2 + 9
-
5Semplifica entrambi i lati. Scomponi in fattori un lato (il sinistro nell'esempio). La forma scomposta sarà (x - b/2)2. Somma i termini simili tra loro (a destra nell'esempio).(x - 3)(x - 3) = 9/2 + 18/2(x - 3)2 = 27/2
-
6Calcola la radice quadrata di entrambi i lati. Non dimenticare di aggiungere il segno più o meno (±) al lato della constante.x - 3 = ±√(27/2)
-
7Semplifica la radice e risolvi per la x.x - 3 = ±3√(6) ------- 2x = 3 ±3√(6) ------- 2Pubblicità
Consigli
- Se il numero sotto la radice quadrata non è un quadrato perfetto, allora gli ultimi passaggi sono un po' diversi.
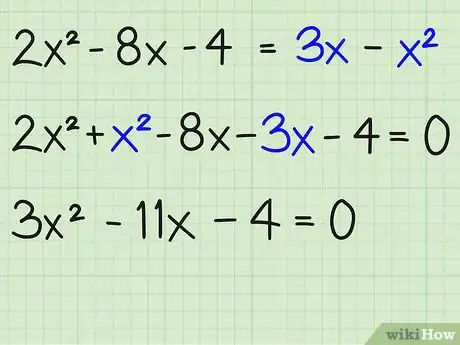
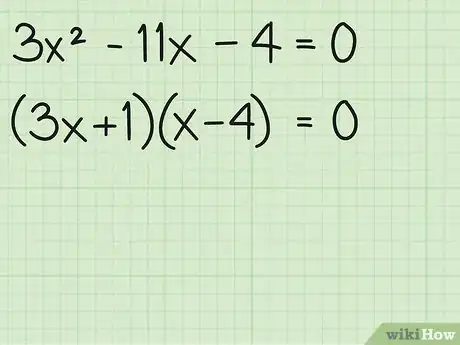
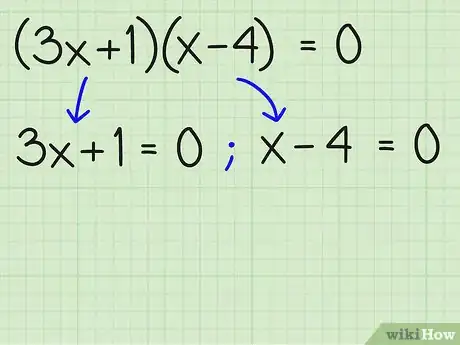
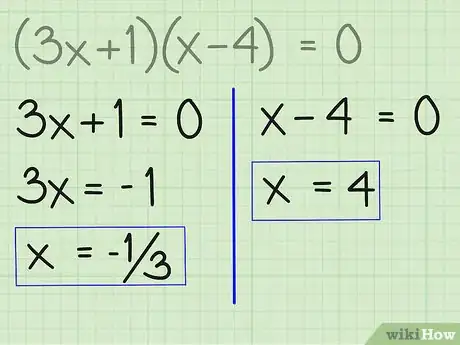
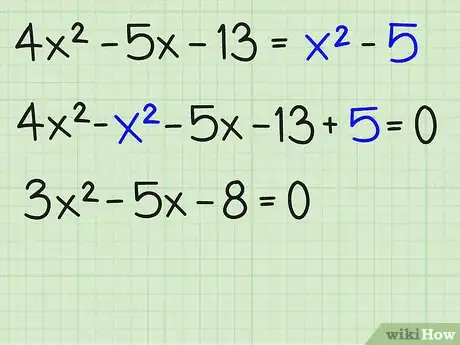
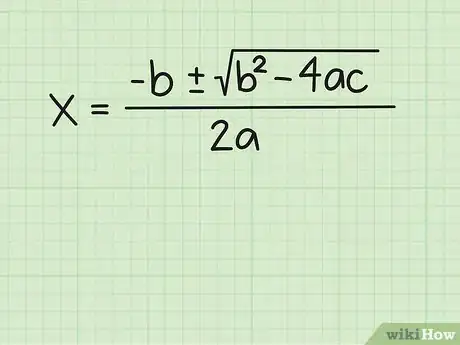
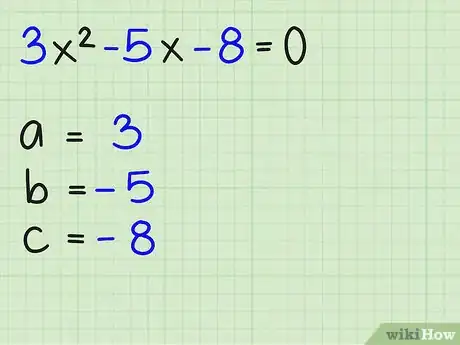
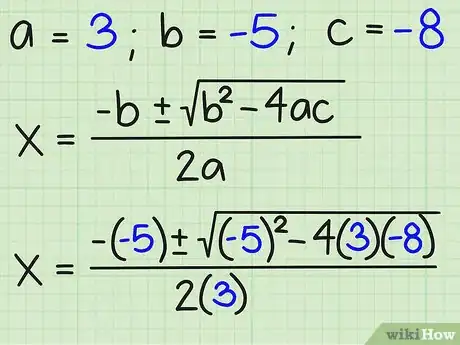
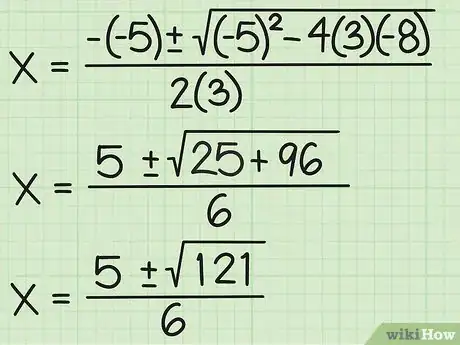
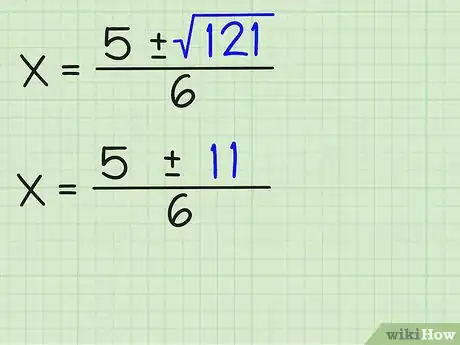

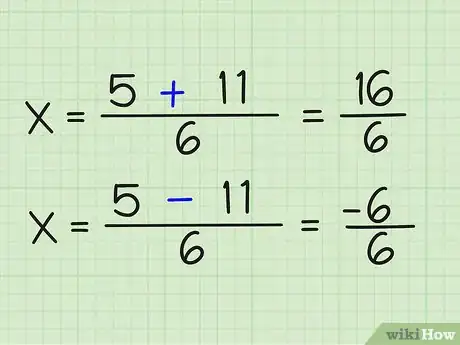

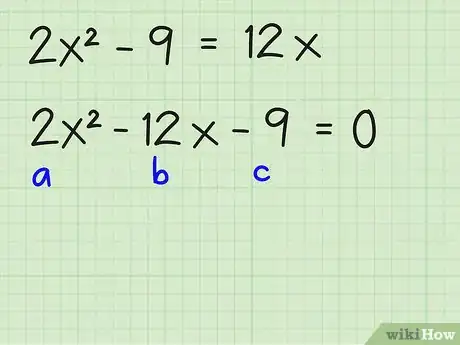
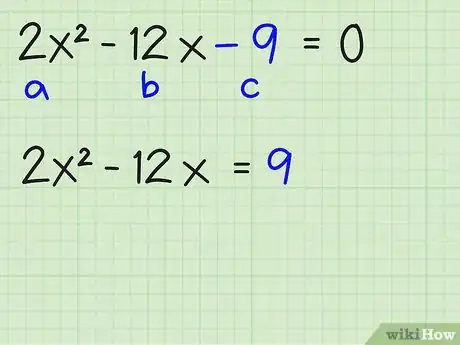
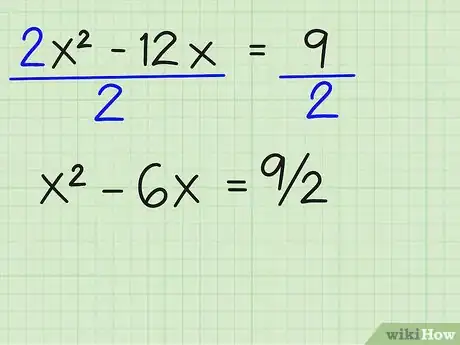
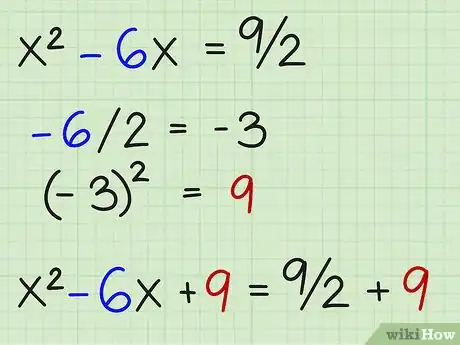
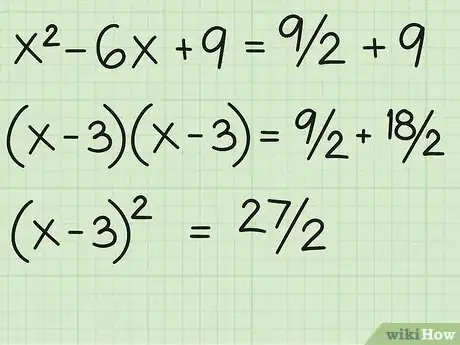
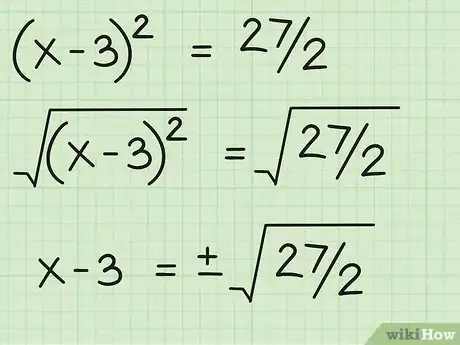
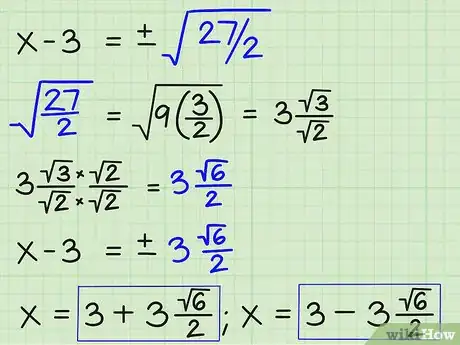
-Step-31-Version-2.webp)





-to-Grams-(g)-Step-12-Version-4.webp)






-Step-31-Version-2.webp)



