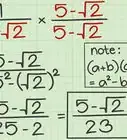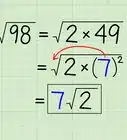X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 26 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 56 818 volte
Per poter sommare e sottrarre fra loro le radici quadrate, queste devono avere lo stesso radicando. In altre parole, puoi sommare o sottrarre 2√3 con 4√3 ma non 2√3 con 2√5. Ci sono molte situazioni in cui puoi semplificare il numero sotto radice per poter procedere alle operazioni di somma e sottrazione.
Passaggi
Parte 1
Parte 1 di 2:
Comprendere le Basi
-
1Quando possibile, semplifica ogni valore sotto radice. Per eseguire questa operazione, devi scomporre il radicando in fattori per trovarne almeno uno che sia un quadrato perfetto, come 25 (5 x 5) o 9 (3 x 3). A questo punto, puoi estrarre dal segno di radice il quadrato perfetto e scriverlo alla sinistra del radicale lasciando gli altri fattori all’interno. Per esempio consideriamo il problema: 6√50 - 2√8 + 5√12. I numeri esterni alla radice sono detti coefficienti e i numeri sotto il segno di radice radicandi. Ecco come puoi procedere alla semplificazione:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Hai scomposto in fattori il numero "50" trovando "25 x 2", hai estratto dalla radice il "5" del quadrato perfetto "25" e lo hai posto alla sinistra del radicale. Il numero "2" è rimasto sotto radice. Ora moltiplica "5" per "6", il coefficiente che già si trova fuori radice, e ottieni 30.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. In questo caso hai scomposto "8" in "4 x 2", hai estratto "2" dal quadrato perfetto "4" e lo hai scritto a sinistra del radicale lasciando "2" all’interno. A questo punto moltiplica "2" per "2", il numero che già si trova fuori dalla radice, e ottieni 4 come nuovo coefficiente.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Scomponi "12" in "4 x 3" ed estrai "2" dal quadrato perfetto "4". Scrivilo alla sinistra della radice lasciando "3" all’interno. Moltiplica "2" per "5", il coefficiente già presente fuori dal radicale, e ottieni 10.
-
2Cerchia ogni termine dell’espressione che ha lo stesso radicando. Una volta eseguite tutte le semplificazioni, otterrai: 30√2 - 4√2 + 10√3. Poiché puoi sommare o sottrarre solo i termini con il medesimo radicando, dovresti cerchiarli per renderli più visibili. Nel nostro esempio si tratta di: 30√2 e 4√2. Puoi pensare a questa operazione come alla sottrazione e somma fra frazioni dove puoi combinare solo quelle con il medesimo denominatore.
-
3Se stai calcolando un'espressione più lunga e ci sono molti fattori con radicandi comuni, puoi cerchiare una coppia, sottolinearne un’altra, aggiungere un asterisco alla terza e così via. Riscrivi i termini dell’espressione in modo che sia più semplice visualizzare la soluzione.
-
4Sottrai o somma fra loro i coefficienti con lo stesso radicando. Ora puoi procedere alle operazioni di somma/sottrazione e lasciare immutate le altre parti dell’equazione. Non combinare i radicandi. Il concetto alla base di questa operazione è quello di scrivere quante radici con il medesimo radicando sono presenti nell’espressione. I valori non-simili devono rimanere da soli. Ecco cosa devi fare:
- 30√2 - 4√2 + 10√3 =
- (30 - 4)√2 + 10√3 =
- 26√2 + 10√3
Pubblicità
Parte 2
Parte 2 di 2:
Esercitarsi
-
1Primo esercizio. Somma le seguenti radici: √(45) + 4√5. Ecco il procedimento:
- Semplifica √(45). Per prima cosa scomponi in fattori il numero 45 e ottieni: √(9 x 5).
- Estrai il numero "3" dal quadrato perfetto "9" e scrivilo come coefficiente del radicale: √(45) = 3√5.
- Ora somma fra loro i coefficienti dei due termini che hanno il radicando comune e otterrai la soluzione: 3√5 + 4√5 = 7√5
-
2Secondo esercizio. Risolvi l’espressione: 6√(40) - 3√(10) + √5. Ecco come dovresti procedere:
- Semplifica 6√(40). Scomponi "40" in "4 x 10" e ottieni che 6√(40) = 6√(4 x 10).
- Estrai "2" dal quadrato perfetto "4" e moltiplicalo per il coefficiente esistente. Ora hai: 6√(4 x 10) = (6 x 2)√10.
- Moltiplica fra loro i coefficienti:12√10.
- Ora rileggi il problema: 12√10 - 3√(10) + √5. Dato che i primi due termini hanno uguale radicando, puoi procedere alla sottrazione, ma dovrai lasciare immutato il terzo termine.
- Otterrai:(12-3)√10 + √5 che può essere semplificato con 9√10 + √5.
-
3Terzo esercizio. Risolvi la seguente espressione: 9√5 -2√3 - 4√5. In questo caso non ci sono radicandi con quadrati perfetti e non è possibile alcuna semplificazione. Il primo e il terzo termine hanno lo stesso radicando, quindi possono essere sottratti fra loro (9 - 4). I radicandi restano uguali. Il secondo termine non è simile e viene riscritto tale e quale: 5√5 - 2√3.
-
4Quarto esercizio. Risolvi la seguente espressione: √9 + √4 - 3√2. Ecco il procedimento:
- Dato che √9 è pari a √(3 x 3), puoi semplificare √9 in 3.
- Dato che √4 è pari a √(2 x 2), puoi semplificare √4 in 2.
- Ora svolgi la semplice somma: 3 + 2 = 5.
- Poiché 5 e 3√2 non sono termini simili, non c’è modo di sommarli fra loro. La soluzione finale è: 5 - 3√2.
-
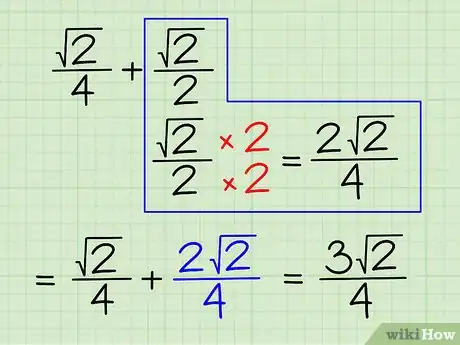
5Quinto esercizio. In questo caso sommiamo e sottraiamo radici quadrate che fanno parte di una frazione. Proprio come nelle normali frazioni, puoi eseguire somme e sottrazioni solo fra quelle con denominatore comune. Supponiamo di risolvere: (√2)/4 + (√2)/2. Ecco il procedimento:
- Fai in modo che i termini abbiano lo stesso denominatore. Il minimo comune denominatore, il denominatore che è divisibile per entrambi i denominatori "4" e "2", è "4".
- Ricalcola il secondo termine, (√2)/2, con il denominatore 4. Per farlo devi moltiplicare sia il numeratore che il denominatore per 2/2. (√2)/2 x 2/2 = (2√2)/4.
- Somma fra loro i numeratori delle frazioni lasciando immutato il denominatore. Procedi come una normale somma fra frazioni: (√2)/4 + (2√2)/4 = 3√2)/4.
Pubblicità
Consigli
- Semplifica sempre i radicandi con un fattore che sia un quadrato perfetto, prima di iniziare a combinare i radicandi simili.
Pubblicità
Avvertenze
- Non sommare o sottrarre mai tra loro dei radicali non simili.
- Non combinare numeri interi e radicali; ad esempio non è possibile semplificare 3 + (2x)1/2.
- Nota: "(2x) elevato a 1/2" = (2x)1/2 è un altro modo di scrivere "radice quadrata di (2x)".
Pubblicità
Informazioni su questo wikiHow
Pubblicità
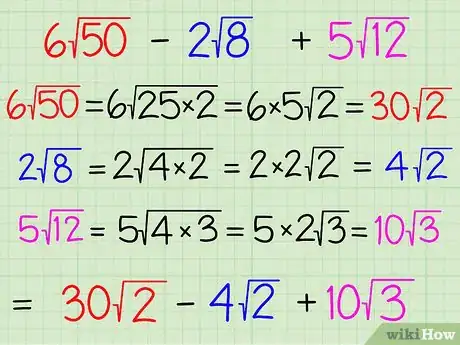


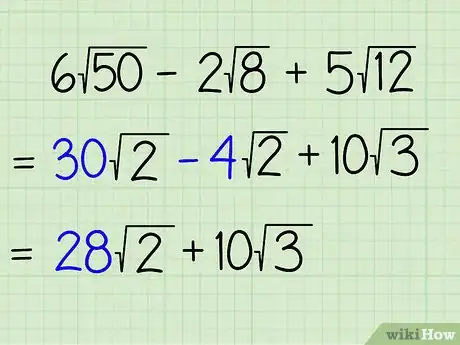






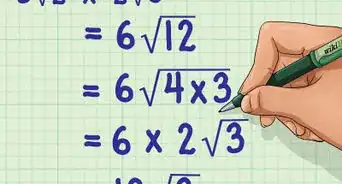
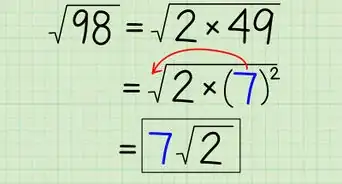



-to-Grams-(g)-Step-12-Version-4.webp)