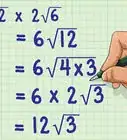Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 28 355 volte
Saper eseguire la divisione fra radici quadrate è un'operazione essenziale per poter semplificare le frazioni che includono radicali. La presenza di questi elementi rende ovviamente l'intero procedimento leggermente più complesso, ma l'uso di regole specifiche permette di gestire le frazioni di radicali in un modo relativamente semplice. Il fattore chiave da tenere sempre a mente consiste nel fatto che è possibile dividere le entità di pari natura, cioè i coefficienti con i coefficienti e i radicandi con i radicandi. Inoltre, ricorda che la forma canonica relativa ai radicali prevede che non appaiano mai al denominatore di una frazione che rappresenta la soluzione finale di un problema.
Passaggi
Dividere i Radicandi
-
1Imposta la frazione. Se l'espressione a cui devi lavorare non è già scritta sotto forma di frazione, devi riscriverla in tal modo. Si tratta di un'operazione che semplifica l'esecuzione di tutti i passaggi necessari a dividere un'espressione per una radice quadrata. Ricorda che, in matematica, la linea che separa il numeratore dal denominatore di una frazione rappresenta a tutti gli effetti una divisione.[1]
- Ad esempio, ipotizzando di dover affrontare il seguente calcolo , il primo passo prevede di riscrivere l'espressione come segue: .
-
2Usa un simbolo di radice unico. Se il problema in esame contiene esclusivamente radici quadrate sia al numeratore sia al denominatore, è possibile inserire i radicandi sotto un unico segno di radice (il radicando è l'argomento del radicale, cioè il numero o l'espressione matematica che appare all'interno del segno di radice).[2] In questo modo si facilita notevolmente il processo di semplificazione.
- Facendo riferimento al nostro esempio, la frazione può essere riscritta nella seguente forma: .
-
3Procedi nel dividere i radicandi. Esegui la divisione dei numeri presenti all'interno del segno di radice, come faresti nel caso di semplici numeri interi. Ricorda che il quoziente della divisione dovrà comunque rimanere il radicando di un radicale, quindi dovrà essere posto all'interno del segno di radice.
- Nel nostro esempio otterremo , quindi il risultato finale del problema iniziale è .
-
4Se necessario, esegui tutte le semplificazioni possibili. Se il radicando rappresenta un quadrato perfetto o se uno dei suoi fattori è un quadrato perfetto, devi semplificare l'espressione. Un quadrato perfetto rappresenta il risultato del prodotto di un numero intero per se stesso.[3] Ad esempio, il numero 25 è un quadrato perfetto perché è il risultato del seguente prodotto: .
- Nel nostro esempio il numero 4 è un quadrato perfetto, dato che . Possiamo quindi semplificare il nostro risultato finale ottenendo:
A questo punto, possiamo affermare che .
Pubblicità - Nel nostro esempio il numero 4 è un quadrato perfetto, dato che . Possiamo quindi semplificare il nostro risultato finale ottenendo:
Fattorizzare i Radicandi
-
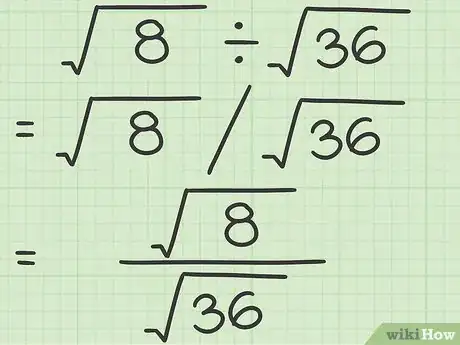
1Riscrivi il problema sotto forma di frazione. Molto probabilmente l'espressione che devi risolvere è già in questa forma, ma in caso contrario riscrivila come frazione. Affrontare il problema dato sotto forma di frazione rende l'intera serie di passaggi molto più semplice, soprattutto quando si deve eseguire la fattorizzazione di una radice quadrata. Ricorda che, in matematica, la linea che separa il numeratore dal denominatore di una frazione rappresenta a tutti gli effetti una divisione.[4]
- Ad esempio, ipotizzando di dover eseguire questo calcolo, , riscriveremo il problema nella forma seguente: .
-
2Scomponi ogni radicando nei suoi fattori. Esegui questo passaggio come faresti nel caso di un qualunque numero intero, avendo l'accortezza di scrivere il risultato ottenuto all'interno del segno di radice.[5]
- Nel nostro esempio otterremo:
- Nel nostro esempio otterremo:
-
3Semplifica il numeratore e il denominatore della frazione ottenuta. La semplificazione di una radice quadrata prevede di estrarre dal segno di radice tutti i radicandi che rappresentano un quadrato perfetto; nel nostro caso, dovremo quindi semplificare tutti i fattori che rappresentano un quadrato perfetto. Ricorda che un quadrato perfetto rappresenta il prodotto di un numero intero per se stesso.[6] I radicandi che possono essere estratti dal segno di radice andranno a comporre il coefficiente della radice quadrata.
- Nel nostro esempio otterremo:
Quindi
- Nel nostro esempio otterremo:
-
4Se necessario, razionalizza il denominatore. La forma canonica in cui devono essere espressi i radicali, prevede che al denominatore di una frazione non compaia mai un segno di radice. Se il risultato che hai ottenuto presenta un radicale al denominatore di una frazione, devi eseguire la relativa razionalizzazione. In pratica, bisogna fare in modo che il segno di radice venga eliminato dal denominatore della frazione in esame. Per farlo, occorre moltiplicare il numeratore e il denominatore della frazione per il radicale che dobbiamo eliminare.[7]
- Ad esempio, nel caso dell'espressione , dobbiamo moltiplicare il numeratore e il denominatore per la , in modo da eliminare il radicale presente al denominatore:
.
- Ad esempio, nel caso dell'espressione , dobbiamo moltiplicare il numeratore e il denominatore per la , in modo da eliminare il radicale presente al denominatore:
-
5Se necessario, esegui tutte le ulteriori semplificazioni. A volte, si ottengono coefficienti che possono essere semplificati fra loro o che possono essere ridotti ai minimi termini. Semplifica i coefficienti presenti al numeratore e al denominatore dell'espressione ottenuta, esattamente come faresti per qualunque altra frazione.
- Nel nostro esempio, la frazione può essere semplificata in , quindi l'espressione può essere riscritta come , o più semplicemente .
Pubblicità
Dividere Radici Quadrate con Coefficienti
-
1Semplifica i coefficienti dei radicali. Si tratta dei numeri posti di fronte al segno di radice. Per semplificarli, dividili o riducili ai minimi termini, come se fossero dei semplici numeri, ignorando per il momento i relativi radicali.
- Ad esempio, ipotizzando di dover eseguire il seguente calcolo , dovremo per prima cosa semplificare la frazione composta dai coefficienti dei radicali . In questo caso, sia il numeratore sia il denominatore sono divisibili per 2, quindi possiamo ridurli come segue: .
-
2Semplifica le radici quadrate. Se l'espressione presente al numeratore è interamente divisibile per quella presente al denominatore, esegui semplicemente la divisione fra i due radicandi. In caso contrario, procedi semplificando ogni radicale, come faresti normalmente.
- Nel nostro esempio, dato che 32 è divisibile per 16, possiamo eseguire la divisione dei due radicandi ottenendo:
-
3Moltiplica i coefficienti ridotti ai minimi termini per il risultato ottenuto dalla semplificazione delle radici quadrate. Ricorda che non è possibile avere un radicale al denominatore di una frazione; quando moltiplichi una frazione per un radicale, quest'ultimo andrà quindi riportato al numeratore.
- Nel nostro esempio, otterremo:
-
4Se necessario, elimina i radicali presenti al denominatore della frazione. Questo passaggio viene chiamato razionalizzazione del denominatore. La forma canonica in cui devono essere espressi i radicali prevede che al denominatore di una frazione non compaia mai un segno di radice. Per razionalizzare il denominatore di una frazione, occorre moltiplicare il relativo numeratore e denominatore per il radicale da eliminare.[8]
- Ad esempio, ipotizzando di dover razionalizzare la seguente espressione , abbiamo la necessità di moltiplicare sia il numeratore che il denominatore per , ottenendo:
Pubblicità - Ad esempio, ipotizzando di dover razionalizzare la seguente espressione , abbiamo la necessità di moltiplicare sia il numeratore che il denominatore per , ottenendo:
Eseguire una Divisione con un Binomio che Contiene un Radicale
-
1Determina se il denominatore della frazione in esame è un binomio. Il denominatore di una frazione è il numero o l'espressione che appare nella parte inferiore della linea divisoria e che rappresenta il divisore. Un binomio è un polinomio composto da due termini.[9] Questo metodo può essere applicato solo alle divisioni fra radici quadrate che presentano un binomio al denominatore.
- Ad esempio, ipotizziamo di dover eseguire la seguente operazione . Al denominatore della frazione abbiamo un binomio, dato che l'espressione non è altro che un polinomio composto da due termini.
-
2Individua il coniugato del binomio in esame. Il coniugato di un binomio è a sua volta un binomio, in cui l'operatore matematico è stato invertito.[10] L'utilizzo del coniugato del binomio originale permette di eliminare la radice quadrata dal denominatore della frazione.
- Nel nostro esempio, i binomi e sono coniugati fra loro, dato che presentano gli stessi termini ma con segno opposto.
-
3Moltiplica il numeratore e il denominatore della frazione per il binomio coniugato del denominatore. In questo modo avrai la possibilità di eliminare il radicale dal denominatore, dato che il prodotto di un binomio per il suo coniugato rappresenta la differenza della radice quadrata di ogni termine del binomio, cioè .[11] .
- Nel nostro esempio, otterremo:
A questo punto, possiamo affermare che .
Pubblicità - Nel nostro esempio, otterremo:
Consigli
- Molte calcolatrici scientifiche consentono di inserire le frazioni nella loro forma naturale premendo un apposito tasto. Prova a digitare il coefficiente del numeratore, premi il tasto in esame e infine inserisci il valore relativo al denominatore. Premendo il tasto "=", la calcolatrice dovrebbe eseguire automaticamente la semplificazione visualizzando la frazione ridotta ai minimi termini.
- Quando si lavora con le radici quadrate, è sempre meglio usare le frazioni improprie, anziché adottare la forma che prevede l'uso dei numeri misti.
- A differenza delle addizioni e delle sottrazioni, quando si affronta una divisione fra radicali, i radicandi non vanno prima necessariamente semplificati allo scopo di estrarre dalla radice i quadrati perfetti. Nella pratica, in questi casi, spesso è meglio eseguire le semplificazioni solo dopo aver raggiunto il risultato finale.
Avvertenze
- Non lasciare mai un radicale al denominatore di una frazione. In questi casi, attua le semplificazioni necessarie o razionalizzalo.
- Non usare mai numeri decimali o misti come coefficienti di un radicale. Convertili in numeri frazionari e apporta le semplificazioni necessarie all'intera espressione in esame.
- Non inserire mai un numero decimale in una frazione. Matematicamente parlando, significherebbe che il denominatore o il numeratore di una frazione sarebbe anch'esso una frazione.
- Se al denominatore di una frazione è presente una somma o una sottrazione di radicali, usa i relativi coniugati per rimuovere le radici dal denominatore.
Riferimenti
- ↑ http://www.mathgoodies.com/lessons/fractions/
- ↑ http://www.mathwarehouse.com/algebra/radicals/dividing-square-roots.php
- ↑ http://www.mathwarehouse.com/arithmetic/numbers/what-is-a-perfect-square.php
- ↑ http://www.mathgoodies.com/lessons/fractions/
- ↑ http://www.purplemath.com/modules/radicals4.htm
- ↑ http://www.mathwarehouse.com/arithmetic/numbers/what-is-a-perfect-square.php
- ↑ http://www.purplemath.com/modules/radicals5.htm
- ↑ http://www.purplemath.com/modules/radicals5.htm
- ↑ https://www.mathsisfun.com/definitions/binomial.html
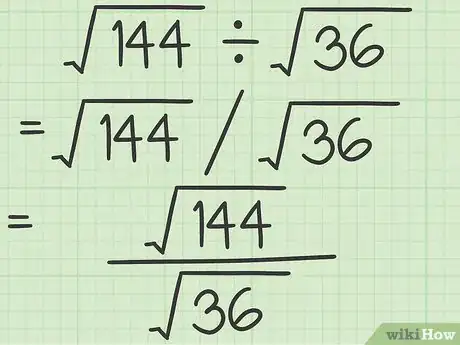




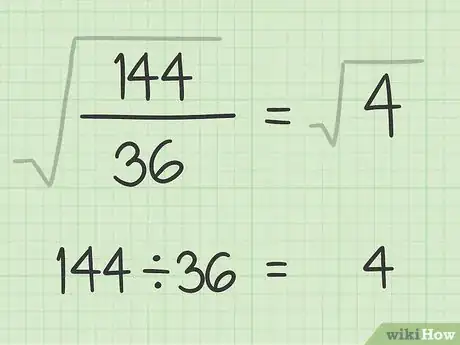


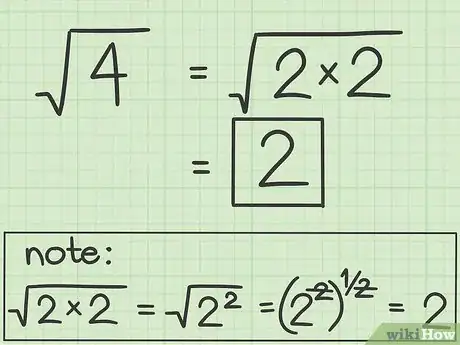








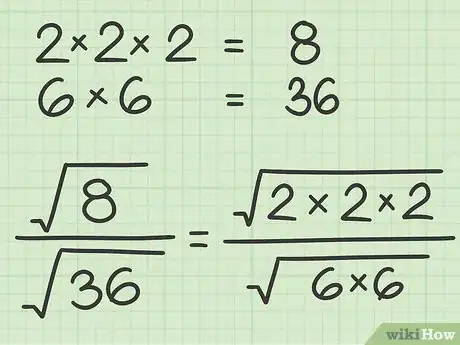

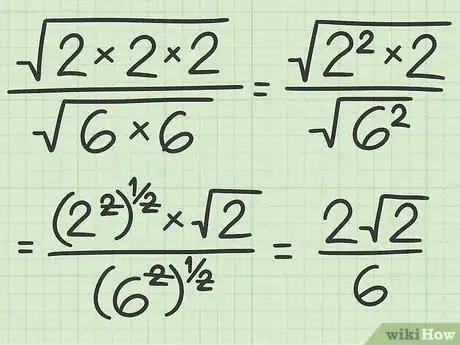



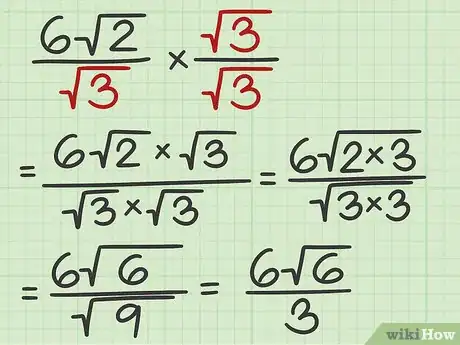






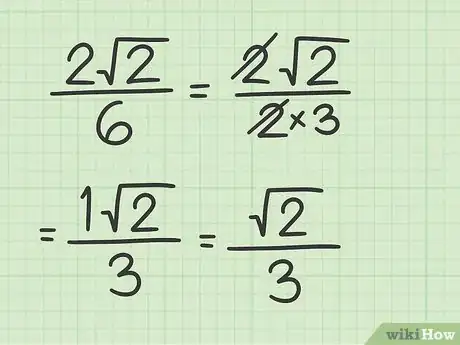




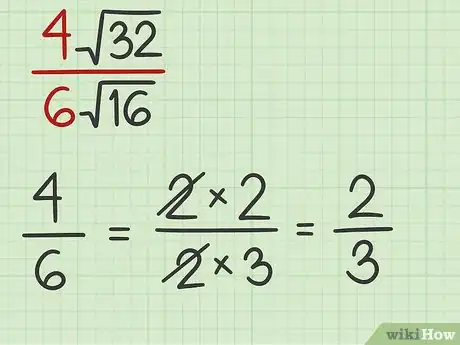



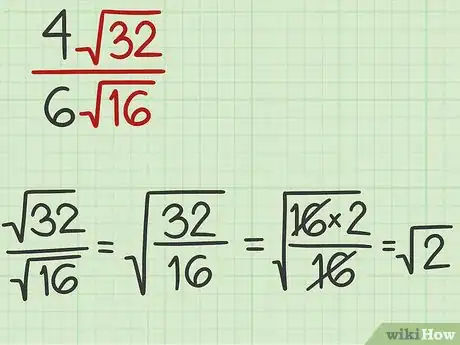

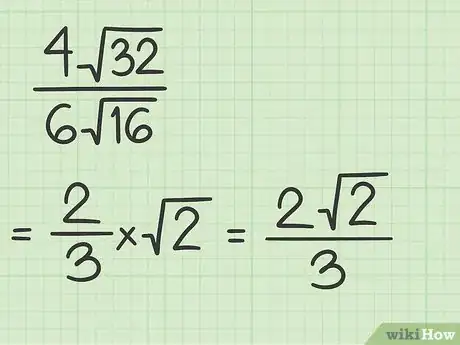

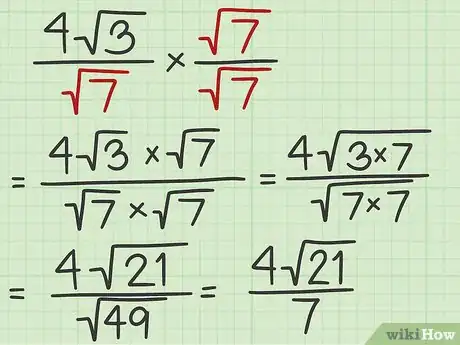









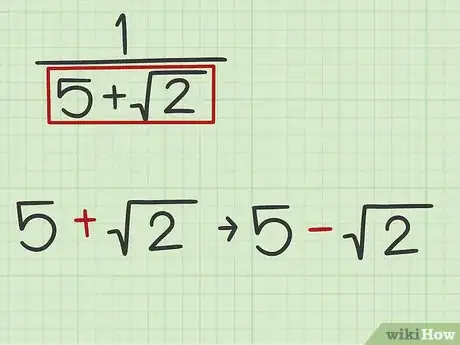














-to-Grams-(g)-Step-12-Version-4.webp)