Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Ci sono 8 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 134 633 volte
Esistono diversi metodi per calcolare le dimensioni di un rettangolo, quale preferire dipende esclusivamente dalle informazioni già note. Conoscendo il valore dell'area superficiale o del perimetro unitamente alla lunghezza di uno dei lati del rettangolo (oppure il rapporto esistente fra altezza e larghezza) è possibile calcolare tutte le altre misure mancanti. Un rettangolo ha proprietà geometriche tali per cui utilizzando uno dei metodi decritti nell'articolo è possibile calcolarne l'altezza o la larghezza.
Passaggi
Utilizzare l'Area Superficiale e la Base
-
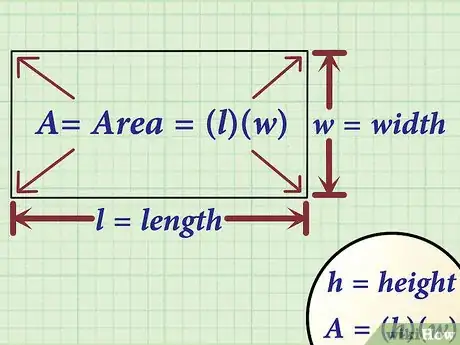
1Imposta la formula per calcolare l'area di un rettangolo. La formula matematica da usare è la seguente , dove rappresenta l'area del rettangolo, rappresenta la base e rappresenta l'altezza.[1]
- Questo metodo è applicabile solo se si conoscono i valori di area e lunghezza della base del rettangolo in esame.
- La formula per il calcolo dell'area potrebbe essere scritta anche nel seguente modo , dove rappresenta la lunghezza del rettangolo (cioè la base) e rappresenta la larghezza (cioè l'altezza). Si tratta solo di una questione di forma, mentre il concetto alla base rimane invariato in entrambe le formule.[2]
-
2Sostituisci il valore dell'area e della base (o lunghezza) all'interno della formula. Assicurati di eseguire la sostituzione dei valori con le variabili corrette.
- Ad esempio, se devi calcolare l'altezza di un rettangolo che ha un'area pari a 24 cm2 e una base di 8 cm, la formula risultante è:
.
- Ad esempio, se devi calcolare l'altezza di un rettangolo che ha un'area pari a 24 cm2 e una base di 8 cm, la formula risultante è:
-
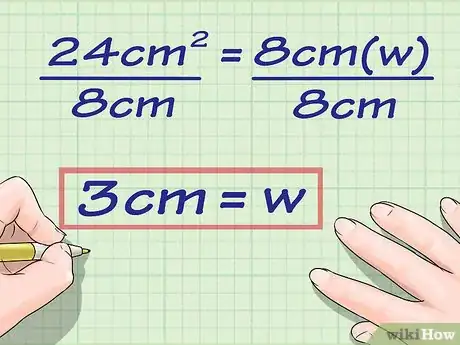
3Risolvi l'equazione in base alla variabile da calcolare, cioè . Per farlo, hai la necessità di dividere entrambi i membri per il valore della base.
- Utilizzando come esempio l'equazione , dovrai dividere ogni membro per 8 ottenendo:
- Utilizzando come esempio l'equazione , dovrai dividere ogni membro per 8 ottenendo:
-
4Riporta il risultato finale senza dimenticarti di includere l'unità di misura.
- Nel nostro esempio il rettangolo con area pari a e base lunga ha un'altezza di .
Pubblicità
Utilizzare il Perimetro e la Base
-
1Imposta la formula per calcolare il perimetro di un rettangolo. La formula matematica da usare è la seguente , dove rappresenta il perimetro del rettangolo in esame, è la base (o la lunghezza) e rappresenta l'altezza o la larghezza della figura.[3]
- Questo metodo è applicabile solo se si conoscono i valori di perimetro e lunghezza della base del rettangolo in esame.
- La stessa formula può essere scritta anche nel seguente modo: (o come nel caso precedente, potrebbero essere riportate la lunghezza e la larghezza del rettangolo che fanno comunque riferimento a base e altezza).[4] Grazie alla proprietà distributiva dell'algebra entrambe le formule, anche se scritte in modo differente, daranno comunque lo stesso risultato.
-
2Sostituisci il valore del perimetro e della lunghezza della base all'interno della formula. Assicurati di eseguire la sostituzione dei valori con le variabili corrette.
- Ipotizzando di dover calcolare l'altezza di un rettangolo avente un perimetro di 22 cm e una base lunga 8 cm, la formula risultante dalla sostituzione dei valori sarà:
- Ipotizzando di dover calcolare l'altezza di un rettangolo avente un perimetro di 22 cm e una base lunga 8 cm, la formula risultante dalla sostituzione dei valori sarà:
-
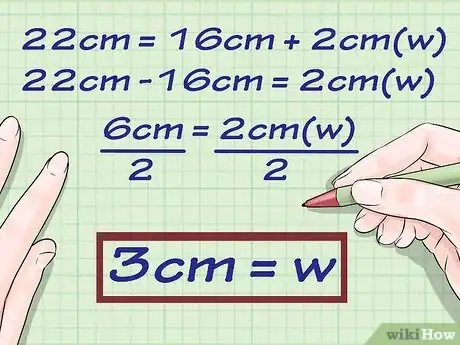
3Risolvi l'equazione in base alla variabile . Per farlo, hai la necessità di sottrarre la lunghezza della base da entrambi i membri dell'equazione per poi dividerli per 2.
- Utilizzando come esempio l'equazione , dovrai sottrarre a entrambi i membri il coefficiente 16 per poi dividerli per 2 ottenendo:
- Utilizzando come esempio l'equazione , dovrai sottrarre a entrambi i membri il coefficiente 16 per poi dividerli per 2 ottenendo:
-
4Riporta il risultato finale senza dimenticare di includere l'unità di misura.
- Nel nostro esempio il rettangolo avente il perimetro pari a e una base lunga possiede un'altezza pari a .
Pubblicità
Utilizzare la Diagonale e la Base
-
1Imposta la formula per calcolare la lunghezza della diagonale di un rettangolo. La formula è espressa dal teorema di Pitagora ed è la seguente: , dove è la lunghezza della diagonale, rappresenta l'altezza e è pari alla lunghezza della base della figura geometrica.[5]
- Questo metodo è applicabile solo se si conoscono la lunghezza della diagonale e della base del rettangolo in esame.
- La formula per il calcolo della lunghezza della diagonale di un rettangolo potrebbe essere scritta anche nel seguente modo , dove rappresenta la larghezza (cioè l'altezza) e rappresenta la lunghezza del rettangolo (cioè la base).[6] Anche in questo caso il risultato finale non cambia, dato che le variabili in gioco fanno riferimento agli stessi valori.
-
2Sostituisci il valore relativo alla lunghezza della diagonale e della base all'interno della formula. Assicurati di eseguire la sostituzione dei valori con le variabili corrette.
- Ipotizzando di dover calcolare l'altezza di un rettangolo avente una diagonale lunga 5 cm e la base lunga 4 cm, la formula risultante dalla sostituzione dei valori sarà:
-
3Eleva al quadrato entrambi i membri dell'equazione. Per poter eliminare la radice quadrata, occorre appunto elevare al quadrato entrambi i membri dell'equazione. In questo modo risolvere la formula in base all'altezza risulterà più semplice.
- Nel nostro esempio otterremo quanto segue:
- Nel nostro esempio otterremo quanto segue:
-
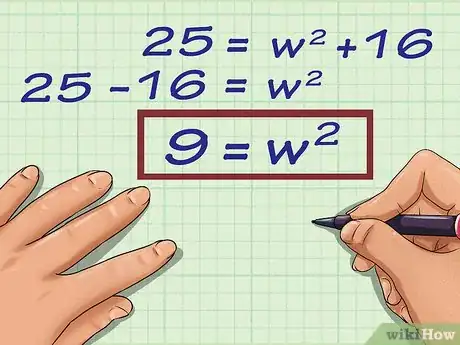
4Isola la variabile all'interno di un membro dell'equazione. Per farlo, devi sottrarre il quadrato della base da ognuno dei membri della formula.
- Utilizzando come esempio l'equazione , dovrai sottrarre il coefficiente 16 da ciascun membro:
- Utilizzando come esempio l'equazione , dovrai sottrarre il coefficiente 16 da ciascun membro:
-
5Risolvi l'equazione in base alla variabile . Per ottenere il risultato finale, devi calcolare la radice quadrata di entrambi i membri dell'equazione.
- Sempre in riferimento al nostro esempio, otterrai:
- Sempre in riferimento al nostro esempio, otterrai:
-
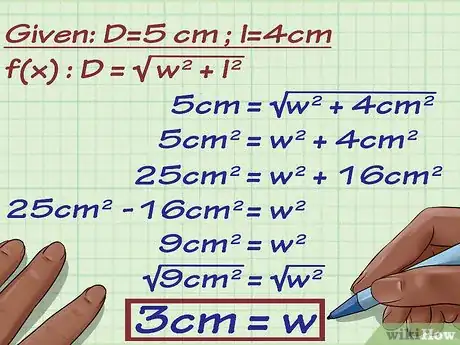
6Riporta il risultato finale senza dimenticarti di includere l'unità di misura.
- Nel nostro esempio il rettangolo avente la diagonale lunga e la base lunga avrà un'altezza pari a .
Pubblicità
Utilizzare l'Area o il Perimetro e il Rapporto fra Base e Altezza
-
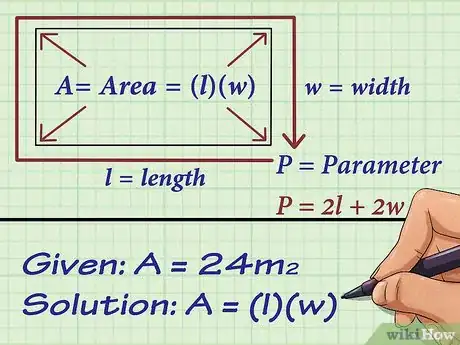
1Imposta la formula per calcolare l'area o il perimetro di un rettangolo. La formula da usare varia in base alle misure conosciute. Se è l'area a essere nota, dovrai utilizzare la formula per il calcolo dell'area; al contrario, utilizzerai la formula per calcolare il perimetro se sarà quest'ultimo il valore noto.
- Se non si conoscono i valori di perimetro, area o il rapporto che lega la base con l'altezza non è possibile applicare questo metodo.
- La formula per calcolare l'area di un rettangolo è .
- La formula per calcolare il perimetro di un rettangolo è .
- Se ad esempio sai che l'area del rettangolo in esame è pari a 24 cm2, puoi impostare la formula per il calcolo dell'area usando i valori noti.
-
2Scrivi l'equazione che descrive il rapporto esistente fra la base e l'altezza di un rettangolo. Scrivi la formula in base alla variabile .
- Il rapporto esistente fra i lati del rettangolo in esame potrebbe essere espresso in base a quante volte la base è maggiore dell'altezza (o viceversa) oppure alla differenza fra le due lunghezze.
- Ad esempio, potrebbe essere noto che la lunghezza della base è superiore di 5 cm a quella dell'altezza, il rapporto che le lega sarebbe quindi espresso dalla formula .
-
3Sostituisci la formula relativa alla variabile all'interno dell'equazione per il calcolo dell'area o del perimetro. A questo punto l'equazione finale dovrebbe contenere solo la variabile , possiamo quindi risolverla in base all'altezza.
- Ipotizzando di studiare un rettangolo avente area pari a 24 cm2 e il rapporto fra base e altezza pari a , la formula finale dovrebbe essere:
- Ipotizzando di studiare un rettangolo avente area pari a 24 cm2 e il rapporto fra base e altezza pari a , la formula finale dovrebbe essere:
-
4Semplifichiamo l'equazione ottenuta. Questo passaggio può essere eseguito in vari modi, in base a come è stato impostato il legame fra base e altezza e all'aver utilizzato la formula per il calcolo dell'area o del perimetro.[7] Poni l'attenzione sul cercare di ottenere un'equazione che ti permetta di calcolare il valore di nel modo più semplice possibile.
- Utilizzando e semplificando l'equazione del nostro esempio , otterrai .
-
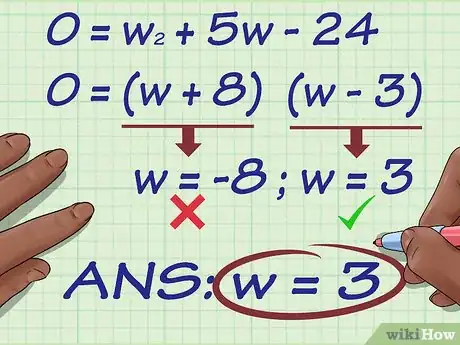
5Risolvi l'equazione in base alla variabile . Anche in questo caso i calcoli da eseguire dipendono da come è stata semplificata l'equazione iniziale nel passaggio precedente. Per procedere, affidati alle proprietà di base dell'algebra e della geometria.
- Potresti dover ricorrere a delle semplici addizioni o divisioni oppure potrebbe essere necessario fattorizzare un'equazione quadratica o usare la formula quadratica.[8]
- Utilizzando l'equazione derivante dal nostro esempio iniziale, possiamo fattorizzarla come segue:
A questo punto i possibili valori della variabile che soddisfano l'equazione sono due: e . Dato che un triangolo non può avere una dimensione negativa possiamo scartare la seconda soluzione e affermare che la nostra risposta finale è .[9]
Pubblicità
Riferimenti
- ↑ http://www.coolmath.com/reference/rectangles#The_area_of_a_rectangle
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.virtualnerd.com/middle-math/geometry-measurement/rectangle-perimeter-area/rectangle-perimeter-example
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://www.coolmath.com/reference/rectangles#The_diagonal_of_a_rectangle
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml







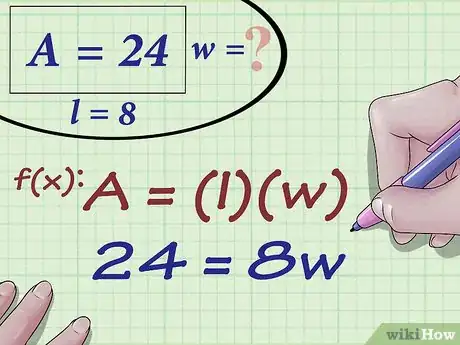











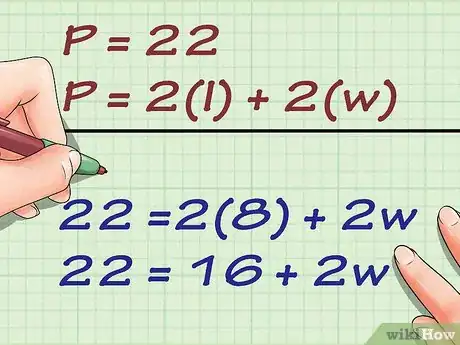


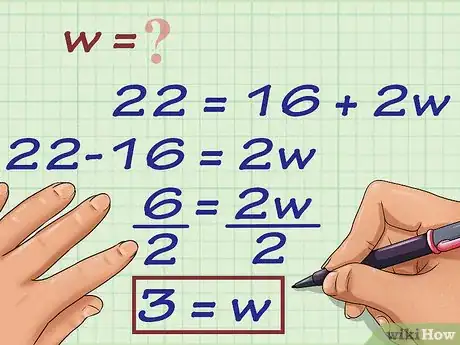



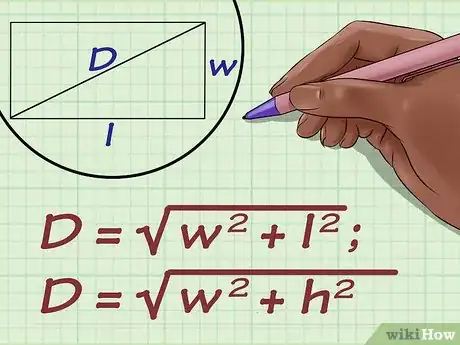



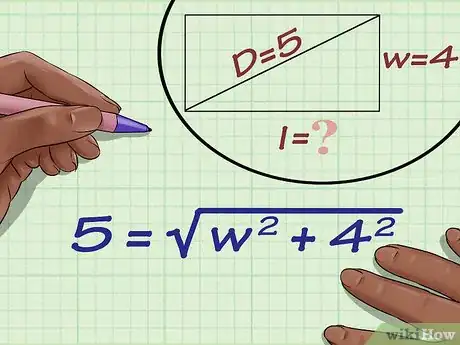

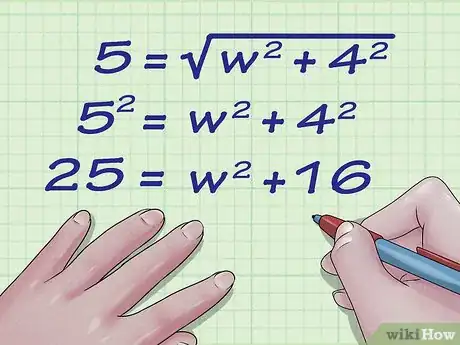




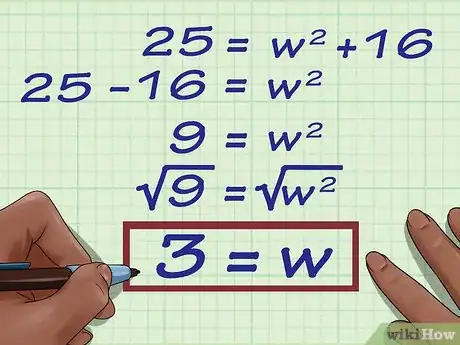





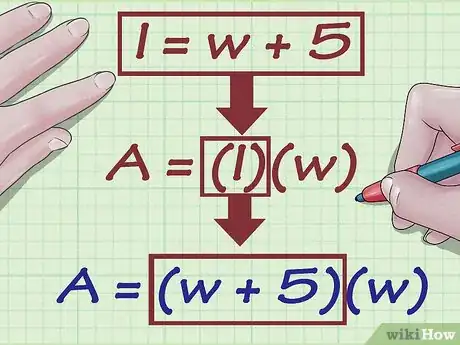









-to-Grams-(g)-Step-12-Version-4.webp)










Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 134 633 volte