Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 99 325 volte
La diagonale di un quadrato rappresenta la linea retta che congiunge un vertice della figura con quello opposto. Per calcolare la lunghezza della diagonale si utilizza la formula , dove rappresenta la lunghezza di un lato del quadrato. Tuttavia, a volte, ti potrebbe venir richiesto di calcolare la lunghezza della diagonale di un quadrato partendo da un altro valore iniziale come ad esempio il perimetro o l'area. In questi casi è necessario partire utilizzando altre formule in modo da poter risalire alla lunghezza del singolo lato che poi andrà utilizzata nella formula per calcolare la diagonale.
Passaggi
Utilizzare la Misura del Lato
-
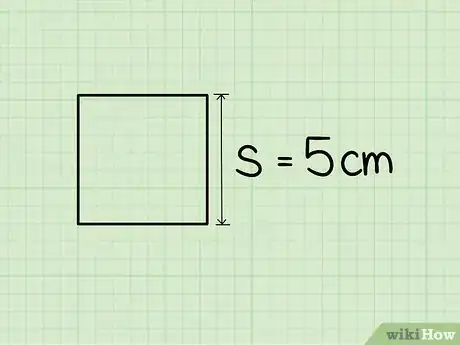
1Individua la lunghezza di un lato del quadrato in esame. Molto probabilmente si tratta di un valore che ti verrà dato come informazione di partenza. Se devi risolvere un problema legato al mondo reale, puoi utilizzare un righello o un metro per ottenere questa misura. Dato che un quadrato è caratterizzato da 4 lati perfettamente identici puoi misurarne uno qualsiasi. Se non conosci la lunghezza di un lato del quadrato in esame non potrai fare affidamento su questo metodo.
- Ad esempio ipotizziamo di voler calcolare la diagonale di un quadrato avente un lato di 5 cm.
-
2Imposta la formula . Nella formula rappresenta la lunghezza della diagonale e quella di un lato del quadrato in esame.[1]
- La formula per il calcolo della diagonale di un quadrato deriva da quella del teorema di Pitagora (). Dato che la diagonale di un quadrato lo suddivide in due triangoli congruenti identici, puoi utilizzare la lunghezza del lato per calcolare quella della diagonale (che rappresenta esattamente l'ipotenusa dei due triangoli).
-
3Sostituisci le variabili della formula con i relativi valori. Assicurati di sostituire la variabile con la misura del lato.
- Ad esempio, se la lunghezza del lato del nostro quadrato è pari a 5 cm la formula finale apparirà così:
.
- Ad esempio, se la lunghezza del lato del nostro quadrato è pari a 5 cm la formula finale apparirà così:
-
4Moltiplica la lunghezza del lato per . In questo modo otterremo la lunghezza della diagonale. È meglio affidarsi a una calcolatrice per eseguire i calcoli dato che ci fornirà un risultato molto più preciso. Se non possiedi una calcolatrice puoi arrotondare il valore di a 1,414.
- Ipotizzando di dover calcolare la lunghezza della diagonale di un quadrato avente il lato di 5 cm la formula finale apparirà così:
Quindi possiamo affermare che la diagonale del nostro quadrato è lunga 7,07 cm.
Pubblicità - Ipotizzando di dover calcolare la lunghezza della diagonale di un quadrato avente il lato di 5 cm la formula finale apparirà così:
Utilizzare il Perimetro
-
1Imposta la formula per calcolare il perimetro di un quadrato. La formula è , dove rappresenta il perimetro e la lunghezza del lato.[2]
- Questo metodo è applicabile solo nel caso in cui si conosca il valore del perimetro del quadrato in esame.
- Per calcolare la lunghezza della diagonale dobbiamo prima di tutto ricavare la misura di un lato, quindi partendo dalla formula del perimetro dobbiamo risolvere l'equazione in base a .
-
2Sostituisci il valore del perimetro all'interno della relativa formula. Assicurati di sostituire la variabile con il relativo valore.
- Ipotizzando di avere un quadrato il cui perimetro è pari a 20 cm, la formula apparirebbe così:
.
- Ipotizzando di avere un quadrato il cui perimetro è pari a 20 cm, la formula apparirebbe così:
-
3Risolvi l'equazione in base a . Per farlo occorre dividere ogni membro per 4. In questo modo otterremo la lunghezza di un singolo lato del quadrato.
- Nel nostro esempio otterremo:
.
- Nel nostro esempio otterremo:
-
4Imposta la formula . In questa formula rappresenta la diagonale del quadrato mentre è pari alla lunghezza di un lato.[3]
- La formula per il calcolo della diagonale di un quadrato deriva da quella del teorema di Pitagora (). Dato che la diagonale di un quadrato lo suddivide in due triangoli congruenti identici, puoi utilizzare la lunghezza del lato per calcolare quella della diagonale (che rappresenta esattamente l'ipotenusa dei due triangoli).
-
5Inserisci la lunghezza del lato all'interno della formula. Assicurati di sostituire la variabile con il relativo valore.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
-
6Moltiplica la lunghezza del lato per . In questo modo otterremo la lunghezza della diagonale. È meglio affidarsi a una calcolatrice per eseguire i calcoli dato che ci fornirà un risultato molto più preciso. Se non possiedi una calcolatrice puoi arrotondare il valore di a 1,414.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
Quindi possiamo affermare che la diagonale del nostro quadrato è lunga 7,07 cm.
Pubblicità - Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
Utilizzare l'Area
-
1Imposta la formula per calcolare l'area di un quadrato. La formula da usare è , dove rappresenta 'area della figura e è la lunghezza di un singolo lato.[4]
- Questo metodo si può applicare solo se si conosce l'area del quadrato in esame.
- Per calcolare la lunghezza della diagonale dobbiamo prima di tutto ricavare la misura di un lato, quindi partendo dalla formula dell'area dobbiamo risolvere l'equazione in base a .
-
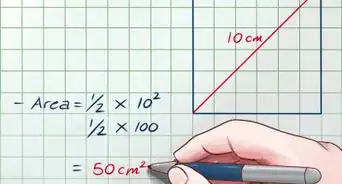
2Sostituisci il valore dell'area all'interno della relativa formula. Assicurati di sostituire la variabile con il relativo valore.
- Ipotizzando di avere un quadrato con un area pari a 25 cm2 la formula apparirà così:
.
- Ipotizzando di avere un quadrato con un area pari a 25 cm2 la formula apparirà così:
-
3Risolvi l'equazione in base a . Per farlo occorre calcolare la radice quadrata dell'area. In questo modo otterremo la lunghezza di un singolo lato. Per eseguire i calcoli è meglio usare una calcolatrice. Se preferisci calcolare la radice quadrata manualmente fai riferimento a questo articolo per avere maggiori dettagli.
- Nel nostro esempio otterremo:
.
- Nel nostro esempio otterremo:
-
4Imposta la formula per calcolare la diagonale . In questa formula rappresenta la diagonale del quadrato mentre è pari alla lunghezza di un lato.[5]
- La formula per il calcolo della diagonale di un quadrato deriva da quella del teorema di Pitagora (). Dato che la diagonale di un quadrato lo suddivide in due triangoli congruenti identici, puoi utilizzare la lunghezza del lato per calcolare quella della diagonale (che rappresenta esattamente l'ipotenusa dei due triangoli).
-
5Inserisci la lunghezza del lato all'interno della formula. Assicurati di sostituire la variabile con il relativo valore.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
-
6Moltiplica la lunghezza del lato per . In questo modo otterremo la lunghezza della diagonale. È meglio affidarsi a una calcolatrice per eseguire i calcoli dato che ci fornirà un risultato molto più preciso. Se non possiedi una calcolatrice puoi arrotondare il valore di a 1,414.
- Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
Quindi possiamo affermare che la diagonale del nostro quadrato è lunga 7,07 cm.
Pubblicità - Nel nostro esempio la lunghezza del lato è pari a 5 cm, quindi la formula finale apparirà così:
Cose che ti Serviranno
- Calcolatrice


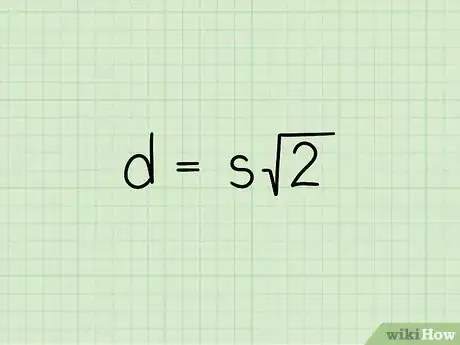


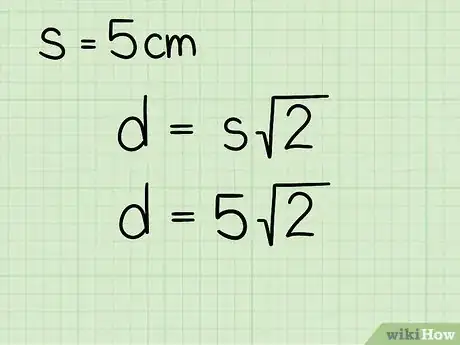

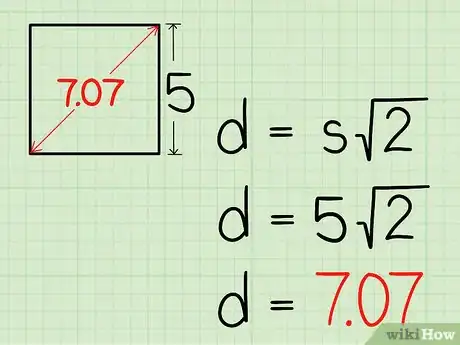











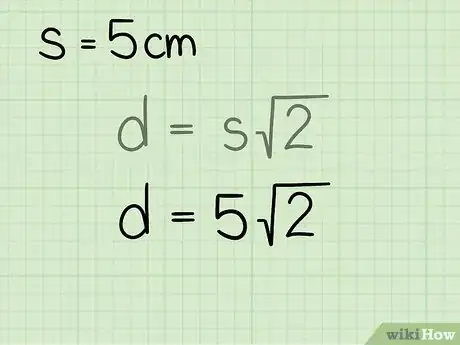
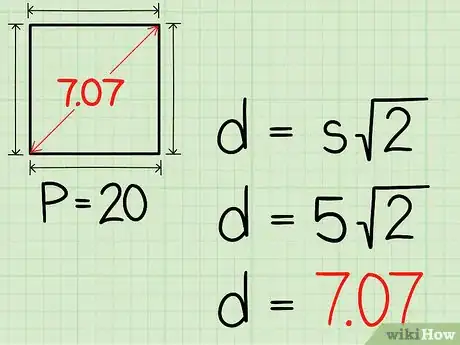
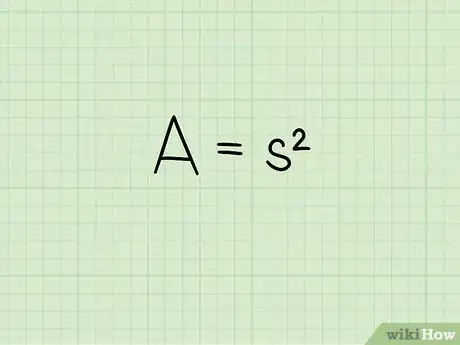






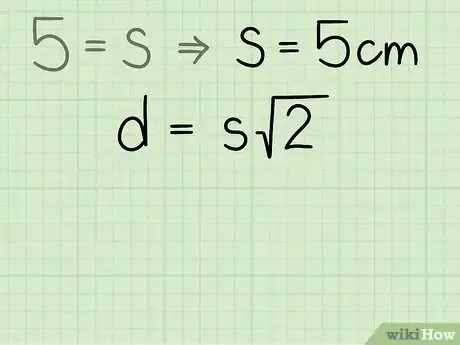

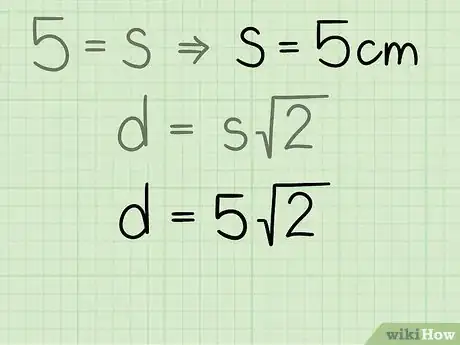




-to-Grams-(g)-Step-12-Version-4.webp)














