Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 21 461 volte
La sequenza di Fibonacci è una serie di numeri che viene generata sommando fra loro i due elementi precedenti della serie. La peculiarità di questa sequenza matematica sta nel fatto che i numeri che la compongono si possono trovare molto spesso anche nella realtà, ad esempio in natura o nelle opere d'arte, e sono rappresentati da spirali e dalla costante denominata "sezione aurea" o "rapporto aureo". Il metodo più semplice per calcolare gli elementi che compongono la sequenza di Fibonacci consiste nel creare manualmente una tabella. Questo sistema risulta tuttavia poco pratico e poco efficiente se si ha la necessità di calcolare il centesimo elemento della sequenza, quindi in questo caso si fa ricorso all'elegante formula matematica di Binet.
Passaggi
Utilizzare una Tabella
-
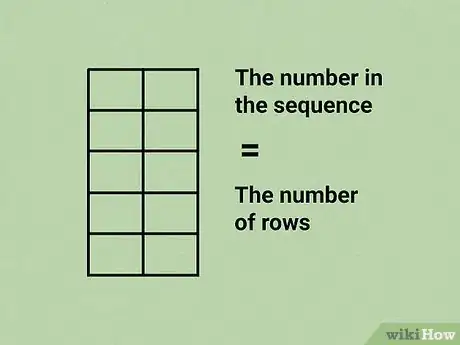
1Imposta una tabella costituita da due colonne. Il numero delle righe che la costituiscono dipende dal numero di elementi della sequenza di Fibonacci che desideri calcolare.
- Ad esempio, se hai la necessità di individuare i primi 5 numeri della successione di Fibonacci, devi creare una tabella con 5 righe.
- Quando utilizzi questo metodo, non è possibile calcolare gli elementi successivi della serie senza aver prima già ottenuto tutti i precedenti. Ad esempio, se vuoi calcolare il centesimo numero della successione di Fibonacci, sei obbligato a trovare prima tutti i 99 numeri che lo precedono. Questo è il motivo per cui questo metodo è ideale per calcolare i primi elementi della serie.
-
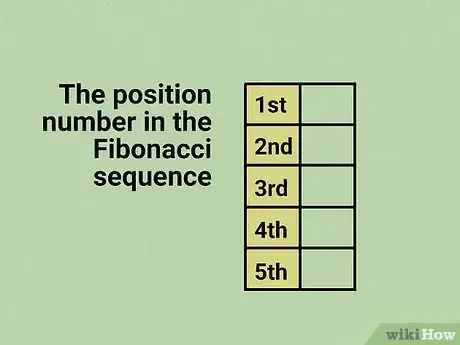
2Inserisci la serie di numeri che identifica gli elementi della sequenza nella prima colonna della tabella. In altre parole, devi semplicemente creare una sequenza ordinata di numeri che parte da 1.
- Ogni numero della sequenza fa riferimento alla posizione del relativo elemento della sequenza di Fibonacci.
- Ad esempio, se hai la necessità di calcolare i primi 5 elementi della successione di Fibonacci, all'interno della prima colonna della tabella (quella di sinistra) devi inserire i numeri 1, 2, 3, 4 e 5. In questo modo potrai facilmente individuare quali sono i primi 5 elementi della sequenza di Fibonacci.
-
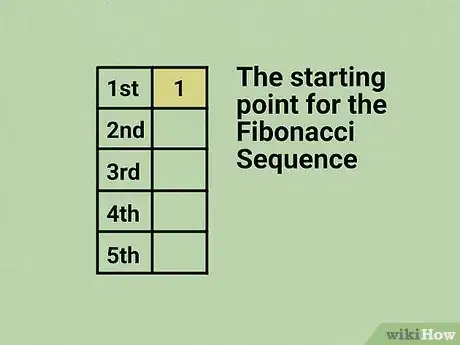
3Nella prima cella della colonna di destra, inserisci il numero "1". Si tratta del punto di partenza per il calcolo della successione di Fibonacci. In altre parole, il primo elemento della serie è rappresentato dal numero 1.
- La sequenza di Fibonacci corretta parte sempre dal numero 1. Nel caso si utilizzi una serie che inizia con un numero differente, non si sta calcolando la successione di Fibonacci.
-
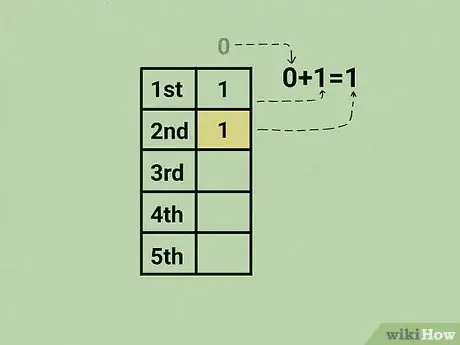
4Somma il primo elemento della serie (1) con 0. In questo modo si calcola il secondo numero della sequenza.
- Ricorda che qualunque numero della successione di Fibonacci è dato dalla somma dei due elementi che lo precedono.
- Per creare la successione di Fibonacci, basta pensare che l'elemento che precede il numero 1 è 0, quindi 0 + 1 = 1.
-
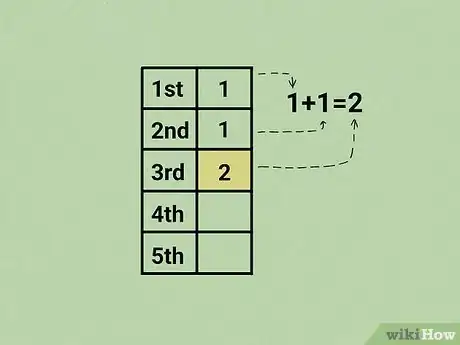
5Somma fra loro il primo elemento della successione (1) e il secondo (1). In questo modo si ottiene come risultato il terzo numero della sequenza di Fibonacci.
- 1 + 1 = 2. Il terzo numero della serie è 2.
-
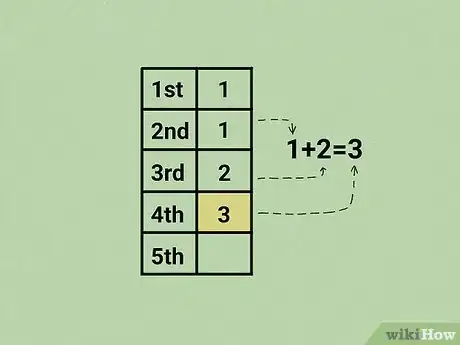
6Per ottenere il quarto numero della successione di Fibonacci, somma fra loro il secondo elemento della sequenza (1) e il terzo (2).
- 1 + 2 = 3. Il quarto numero della serie è 3.
-
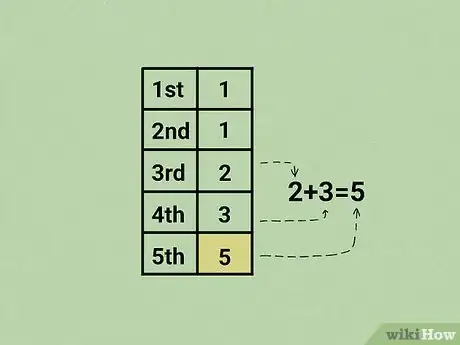
7Somma fra loro il terzo elemento della successione (2) e il quarto (3). In questo modo ottieni il quinto numero che compone la sequenza di Fibonacci.
- 2 + 3 = 5. Il quinto numero della serie è 5.
-
8Per calcolare qualunque numero della successione di Fibonacci, somma i due elementi della serie che lo precedono. Quando applichi questo semplice metodo stai utilizzando la formula matematica .[1] Dato che questa formula è espressa in forma ricorsiva, non può essere usata per calcolare un elemento qualunque della sequenza senza prima aver ottenuto tutti quelli che lo precedono.Pubblicità
Utilizzare la Formula di Binet
-
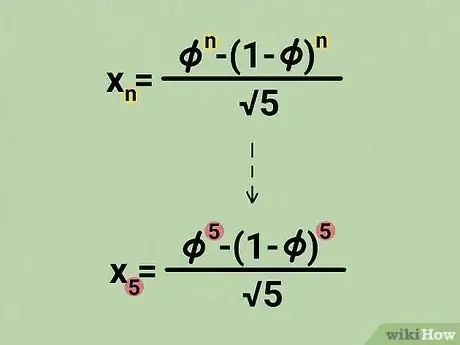
1Imposta la formula matematica di Binet: =. Nella formula, con il termine si indica l'elemento della successione di Fibonacci che si desidera calcolare, rappresenta la posizione occupata dal numero in esame all'interno della sequenza e rappresenta il numero naturale irrazionale denominato "sezione aurea" o "rapporto aureo".[2]
- Questa formula è definita in "forma chiusa", quindi è possibile usarla per calcolare qualunque elemento della sequenza senza la necessità di dover calcolare prima tutti quelli precedenti.
- Questa è una formula semplificata derivata da quella originale creata da Binet.[3]
- La formula in esame utilizza la costante denominata "sezione aurea" (), perché il rapporto fra due elementi successivi qualsiasi della sequenza di Fibonacci, all'infinito, tende alla "sezione aurea".[4]
-
2Sostituisci la variabile della formula con il numero desiderato. Ricorda che rappresenta la posizione dell'elemento della successione di Fibonacci che si desidera calcolare.
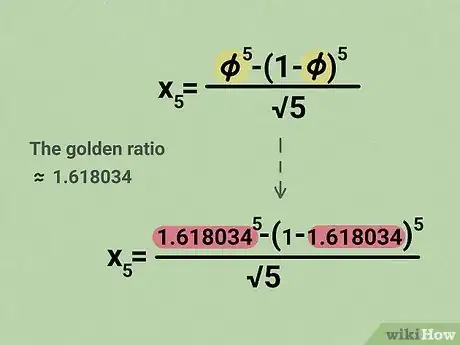
- Ad esempio, se hai la necessità di calcolare il quinto numero della serie, devi usare il numero 5. In questo caso la formula apparirà così: =.
-
3Sostituisci il valore della "sezione aurea" all'interno della formula. Puoi usare un'approssimazione del valore di tale costante che è pari a 1,618034.[5]
- Ad esempio, ipotizzando di voler calcolare il valore del quinto elemento della successione di Fibonacci, la formula finale apparirà così: =.
-
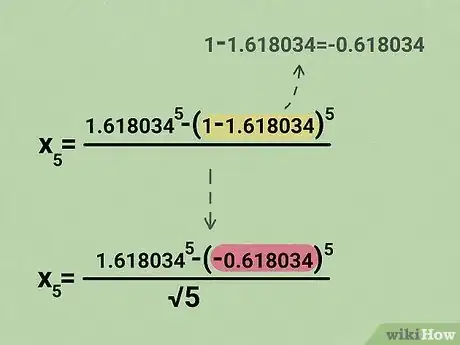
4Calcola per primi i termini presenti all'interno delle parentesi. Ricorda di rispettare sempre l'ordine in cui devono essere svolte le operazioni matematiche; in questo caso, iniziamo quindi a calcolare i termini posti all'interno delle parentesi tonde ottenendo: .
- Nel nostro esempio, l'equazione di partenza è diventata la seguente: =.
-
5Calcola le potenze. Eleva a potenza i due numeri posti all'interno delle parentesi posti al numeratore della frazione utilizzando i rispettivi esponenti.
- Nel nostro esempio, otterremo: e . Al termine, l'equazione di partenza sarà diventata la seguente: .
-
6Completa i calcoli al numeratore eseguendo la sottrazione. Prima di poter calcolare la frazione, hai la necessità di eseguire la sottrazione dei due elementi posti al numeratore.
- Nel nostro esempio, otterremo: . Al termine, la formula di partenza è diventata: =.
-
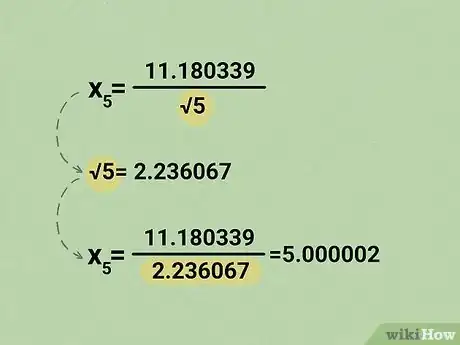
7Dividi il numeratore per la radice quadrata di 5. Il valore arrotondato della radice quadrata di 5 è pari a 2,236067.
- Nel nostro esempio, otterremo quindi: .
-
8Arrotonda il risultato finale al numero intero più prossimo. Il risultato della formula sarà un numero decimale, che tuttavia risulta essere molto vicino a un numero intero, che rappresenta l'elemento della sequenza di Fibonacci che stavi cercando.
- Utilizzando il numero irrazionale completo che corrisponde alla "sezione aurea" e senza compiere alcun arrotondamento si ottiene un numero intero esatto. Per facilitare i calcoli, è molto più pratico eseguire gli arrotondamenti ottenendo in tal modo un risultato decimale.[6]
- Nel nostro esempio, dopo aver eseguito tutti i calcoli con l'aiuto di una calcolatrice, abbiamo ottenuto un risultato pari a 5,000002. Se arrotondiamo quest'ultimo al numero intero più prossimo, otteniamo esattamente la risposta che stavamo cercando, cioè 5: il quinto elemento della successione di Fibonacci.
Pubblicità
Riferimenti
- ↑ http://mathworld.wolfram.com/FibonacciNumber.html
- ↑ https://www.mathsisfun.com/numbers/fibonacci-sequence.html
- ↑ http://mathworld.wolfram.com/FibonacciNumber.html
- ↑ https://www.mathsisfun.com/numbers/fibonacci-sequence.html
- ↑ https://www.mathsisfun.com/numbers/fibonacci-sequence.html
- ↑ https://www.mathsisfun.com/numbers/fibonacci-sequence.html




















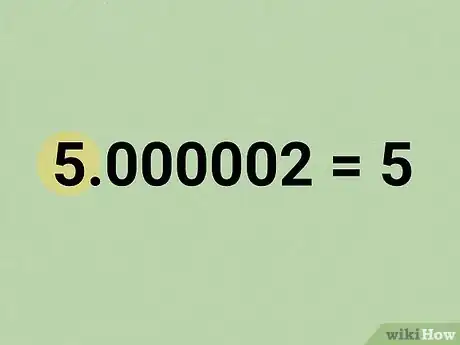



-to-Grams-(g)-Step-12-Version-4.webp)














Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 21 461 volte