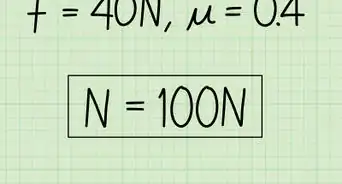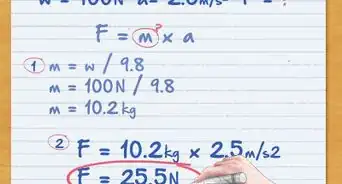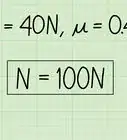Come Calcolare la Tensione in Fisica

Co-redatto da Bess Ruff, MA

In fisica, la tensione è la forza esercitata da una corda, un filo, un cavo e simili su uno o più oggetti. Qualsiasi cosa tirata, appesa, sorretta o fatta oscillare è soggetta alla forza di tensione. Come ogni altra forza, la tensione può far accelerare un oggetto o deformarlo. Essere in grado di calcolare la tensione è importante non solo per gli studenti di fisica ma anche per gli ingegneri e gli architetti i quali, per costruire edifici sicuri, devono conoscere se la tensione su una data corda o cavo possa resistere allo sforzo causato dal peso dell'oggetto prima che ceda e si rompa. Continua a leggere per imparare a calcolare la tensione in diversi sistemi fisici.

Metodo 1

Metodo 1 di 2:

Determinare la Tensione su un'Unica Fune

1
Definisci le forze di entrambe le estremità della fune. La tensione in una data fune è il risultato delle forze che tirano sulla corda da entrambe le estremità. Un piccolo promemoria: forza = massa × accelerazione. Supponendo che la corda sia ben tirata, ogni cambiamento di accelerazione o massa negli oggetti sorretti dalla corda causerà un cambiamento nella tensione della corda. Non dimenticare la costante di accelerazione gravitazionale - anche se un sistema è isolato, le sue componenti sono soggette a questa forza. Prendiamo una data corda, la sua tensione sarà T = (m × g) + (m × a), dove "g" è la costante gravitazionale di ogni oggetto sorretto dalla corda e "a" corrisponde a ogni altra accelerazione su ogni altro oggetto sorretto dalla corda.
- Per la maggior parte dei problemi fisici, supponiamo dei fili ideali - in altre parole, la nostra corda è sottile, senza massa, e non può essere né allungata né spezzata.
- A titolo di esempio, consideriamo un sistema in cui un peso sia attaccato a una trave di legno attraverso un'unica fune (vedi la figura). Il peso e la fune sono immobili - l'intero sistema non si muove. Con queste prerogative sappiamo che, affinché il peso si mantenga in equilibrio, la forza di tensione deve essere equivalente alla forza di gravità esercitata sul peso. In altre parole, Tensione (F_t) = Forza di gravità (F_g) = m × g.
  - Supponiamo di avere un peso da 10 kg, la forza di tensione sarà 10 kg × 9,8 m/s² = 98 Newton.
2
Calcola l'accelerazione. La gravità non è l'unica forza che influisce sulla tensione in una fune, perché qualsiasi forza relativa all'accelerazione di un oggetto a cui è attaccata la fune ne influenza la tensione. Se, ad esempio, un oggetto sospeso viene accelerato da una forza sulla fune o sul cavo, la forza di accelerazione (massa × accelerazione) si aggiunge alla tensione causata dal peso dell'oggetto.
- Facciamo conto che, prendendo l'esempio precedente del peso di 10 kg sospeso con una corda, la fune, invece di essere fissata a una trave di legno, viene usata per tirare verso l'alto il peso con un'accelerazione di 1 m/s². In questo caso, dobbiamo calcolare anche l'accelerazione sul peso, oltre che la forza di gravità, con le seguenti formule:
  - F_t = F_g + m × a
  - F_t = 98 + 10 kg × 1 m/s²
  - F_t = 108 Newton.
3
Calcola l'accelerazione rotazionale. Un oggetto ruotato intorno a un punto centrale tramite l'uso di una fune (come un pendolo) esercita una tensione sulla fune per via della forza centripeta. La forza centripeta è la forza di tensione addizionale che la fune esercita "tirando" verso l'interno per mantenere il movimento di un oggetto dentro al suo arco e non in una linea dritta. Più velocemente si muove un oggetto, maggiore è la forza centripeta. La forza centripeta (F_c) equivale a m × v²/r dove per "m" si intende la massa, per "v" la velocità, mentre "r" è il raggio della circonferenza in cui si inscrive l'arco del movimento dell'oggetto.
- Siccome la direzione e la magnitudine della forza centripeta cambia quando l'oggetto sulla fune si muove e cambia velocità, allo stesso modo cambia la tensione totale sulla fune, che tira sempre in modo parallelo rispetto alla corda verso il centro. Ricorda anche che la forza di gravità influisce costantemente sull'oggetto, "chiamandolo" verso il basso. Per cui, se un oggetto viene ruotato o fatto oscillare verticalmente, la tensione totale è maggiore nella parte inferiore dell'arco (nel caso del pendolo, parliamo di punto di equilibrio) quando l'oggetto si muove a una maggiore velocità e minore nella parte superiore dell'arco quando si muove più lentamente.
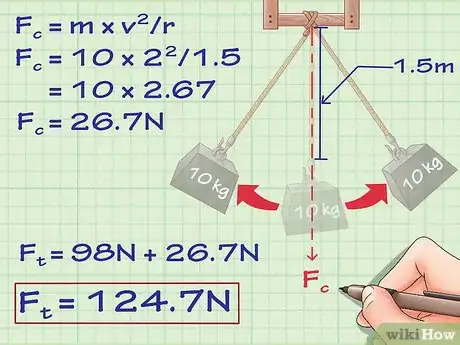
- Riprendiamo il nostro esempio e supponiamo che l'oggetto non stia più accelerando verso l'alto ma che stia oscillando come un pendolo. Mettiamo che la fune sia lunga 1,5 metri e che il nostro peso si muova a 2 m/s quando passa sul punto più basso dell'oscillazione. Se vogliamo calcolare il punto di massima tensione esercitata sulla parte inferiore dell'arco, dovremmo innanzitutto riconoscere che la tensione dovuta alla gravità in questo punto è uguale a quando il peso era immobile - 98 Newton. Per trovare la forza centripeta da aggiungere, dobbiamo usare queste formule:
  - F_c = m × v²/r
  - F_c = 10 × 2²/1,5
  - F_c =10 × 2,67 = 26,7 Newton.
  - Quindi la nostra tensione totale sarà 98 + 26,7 = 124,7 Newton.
4
Sappi che la tensione dovuta alla gravità cambia durante l'oscillazione dell'arco di un oggetto. Come abbiamo detto prima, sia la direzione che la magnitudine della forza centripeta cambia quando un oggetto oscilla. Ad ogni modo, sebbene la forza di gravità rimanga costante, anche la tensione derivante dalla gravità cambia. Quando un oggetto che oscilla non è nella parte inferiore del suo arco (il suo punto di equilibrio), la gravità tira l'oggetto direttamente verso il basso, ma la tensione tira verso l'alto a un certo angolo. Perciò la tensione ha solo la funzione di neutralizzare in parte la forza di gravità, ma non del tutto.
- Dividere la forza di gravità in due vettori può essere utile per visualizzare meglio il concetto. Su ogni dato punto nell'arco di un oggetto che oscilla verticalmente, la fune forma un angolo "θ" con la retta che passa attraverso il punto di equilibrio e il punto centrale della rotazione. Quando il pendolo oscilla, la forza di gravità (m × g) può essere suddivisa in due vettori - mgsin(θ) che è la tangente dell'arco in direzione del punto di equilibrio e mgcos(θ) che è parallelo alla forza di tensione nella direzione opposta. La tensione risponde solo a mgcos(θ) - la forza che gli si oppone - non all'intera forza di gravità (tranne che nel punto di equilibrio, dove sono equivalenti).
- Diciamo che quando il nostro pendolo forma un angolo di 15 gradi con la verticale, si muove a 1,5 m/s. Troveremo la tensione con queste formule:
  - Tensione generata dalla gravità (T_g) = 98cos(15) = 98(0,96) = 94,08 Newtons
  - Forza centripeta (F_c) = 10 × 1,5²/1,5 = 10 × 1,5 = 15 Newtons
  - Tensione totale = T_g + F_c = 94,08 + 15 = 109,08 Newton.
5
Calcola l'attrito. Qualsiasi oggetto attaccato a una corda che subisce una forza di "trascinamento" dovuta all'attrito contro un altro oggetto (o fluido) trasferisce questa forza alla tensione nella fune. La forza data dall'attrito fra due oggetti si calcola come in qualsiasi altra condizione - con la seguente equazione: forza d'attrito (in genere indicata con F_r) = (mu)N, dove mu è il coefficiente d'attrito fra due oggetti e N è la forza normale fra i due oggetti, o la forza che esercitano l'uno sull'altro. Sappi che l'attrito statico - l'attrito generato dalla messa in movimento di un oggetto statico - è diverso dall'attrito dinamico - l'attrito generato dal voler mantenere in movimento un oggetto che è già in movimento.
- Mettiamo che il nostro peso da 10 kg abbia smesso di oscillare e che sia invece adesso trascinato orizzontalmente sul pavimento tramite la nostra fune. Diciamo che il pavimento abbia un coefficiente d'attrito dinamico di 0,5 e che il nostro peso si muova a una velocità costante che vogliamo accelerare a 1 m/s². Questo nuovo problema presenta due cambiamenti importanti - primo, non dobbiamo più calcolare la tensione provocata dalla gravità perché la fune non sta sostenendo il peso contro la sua forza. Secondo, dobbiamo calcolare la tensione causata dall'attrito e quella data dall'accelerazione della massa del peso. Usiamo le seguenti formule:
  - Forza normale (N) = 10 kg × 9,8 (accelerazione dovuta alla gravità) = 98 N
  - Forza data dall'attrito dinamico (F_r) = 0,5 × 98 N = 49 Newton
  - Forza data dall'accelerazione (F_a) = 10 kg × 1 m/s² = 10 Newton
  - Tensione totale = F_r + F_a = 49 + 10 = 59 Newton.
Pubblicità

Metodo 2

Metodo 2 di 2:

Calcolare la Tensione su Più Funi

1
Solleva dei carichi paralleli e verticali usando una puleggia. Le pulegge sono delle macchine semplici costituite da un disco sospeso che consente alla forza di tensione in una fune di cambiare direzione. In una puleggia predisposta in maniera semplice, la corda o il cavo va da un peso all'altro passando attraverso il disco sospeso, creando così due funi con lunghezze diverse. In ogni caso, la tensione in entrambe le parti della corda è equivalente, anche se su ciascuna estremità vengono esercitate delle forze di diversa magnitudine. In un sistema di due masse appese a una puleggia verticale, le tensioni si equivalgono 2g(m₁)(m₂)/(m₂+m₁), dove per "g" si intende l'accelerazione gravitazionale, per "m₁" la massa dell'oggetto 1 e per "m₂" la massa dell'oggetto 2.
- Sappi che, di solito, i problemi di fisica prevedono delle pulegge ideali - pulegge senza massa, senza attrito e che non si possono né rompere né deformare e che sono inseparabili dal soffitto o dal filo che le sorregge.
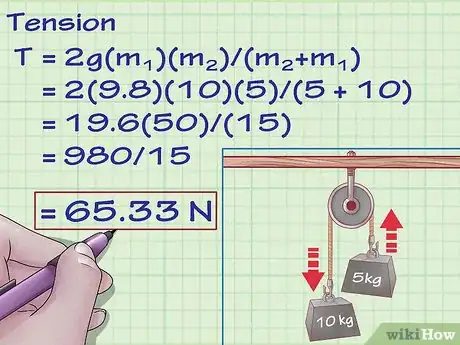
- Mettiamo di avere due pesi che penzolano in verticale da una puleggia, su due funi parallele. Il peso 1 ha una massa di 10 kg, mentre il peso 2 ha una massa di 5 kg. In questo caso troveremo la tensione con queste formule:
  - T = 2g(m₁)(m₂)/(m₂+m₁)
  - T = 2(9,8)(10)(5)/(5 + 10)
  - T = 19,6(50)/(15)
  - T = 980/15
  - T = 65,33 Newton.
- Sappi che siccome un peso è più pesante dell'altro, ed è l'unica condizione che varia nelle due parti della puleggia, questo sistema inizierà ad accelerare, i 10 kg si muoveranno verso il basso e i 5 kg verso l'alto.
2
Solleva dei carichi usando una puleggia con delle funi non parallele. Le pulegge vengono spesso utilizzate per dirigere la tensione in una direzione diversa da "su" e "giù". Se, ad esempio, un peso è sospeso verticalmente dall'estremità di una fune mentre l'altra estremità della fune è attaccata a un secondo peso con un'inclinazione diagonale, il sistema-puleggia non parallelo avrà la forma di un triangolo i cui vertici sono il primo peso, il secondo peso e la puleggia. In questo caso, la tensione nella fune è influenzata sia dalla forza di gravità sul peso che dalle componenti della forza di richiamo parallela alla sezione diagonale della fune.
- Prendiamo un sistema con 10 kg di peso (m₁) che pende in verticale, collegato tramite una puleggia a un peso di 5kg (m₂) su una rampa a 60 gradi (supponi che la rampa sia priva di attrito). Per trovare la tensione nella fune, è più facile procedere prima con il calcolo delle forze che accelerano i pesi. Ecco come fare:
  - Il peso sospeso è più pesante e non abbiamo a che fare con l'attrito, per cui sappiamo che accelera verso il basso. La tensione nella fune tira però verso l'alto, per cui accelera in base alla forza netta F = m₁(g) - T, o 10(9,8) - T = 98 - T.
  - Sappiamo che il peso sulla rampa accelererà percorrendola verso l'alto. Siccome la rampa è priva di attrito, sappiamo che la tensione tira su per la rampa e solo il proprio peso tira verso il basso. L'elemento componente la forza che tira verso il basso sulla rampa è dato da mgsin(θ), quindi nel nostro caso possiamo dire che accelera su per la rampa per via della forza netta F = T - m₂(g)sin(60) = T - 5(9,8)(,87) = T - 42,14.
  - Se facciamo equivalere queste due equazioni, abbiamo 98 - T = T - 42,14. Isolando T avremo 2T = 140,14, ovvero T = 70,07 Newtons.
3
Usa più funi per sorreggere un oggetto sospeso. Per concludere, consideriamo un oggetto sospeso in un sistema di funi "a Y" - due funi sono attaccate al soffitto, e si incontrano su un punto centrale da cui parte una terza fune sulla cui estremità è attaccato un peso. La tensione nella terza fune è ovvia - è semplicemente la tensione provocata dalla forza di gravità, o m(g). Le tensioni nelle altre due funi sono diverse e vanno sommate all'equivalente della forza di gravità per la direzione verticale verso l'alto e a un equivalente zero per entrambe le direzioni orizzontali, supponendo di trovarci in un sistema isolato. La tensione nelle funi è influenzata sia dalla massa del peso sospeso che dall'angolo che forma ogni fune quando incontra il soffitto.
- Supponiamo che il nostro sistema a Y abbia un peso più in basso di 10 kg e che le due corde più in alto incontrino il soffitto formando rispettivamente due angoli di 30 e 60 gradi. Se vogliamo trovare la tensione in ciascuna delle due corde, dovremo considerare per ciascuna gli elementi verticali e orizzontali di tensione. Per risolvere il problema per T₁ (la tensione nella fune a 30 gradi) e T₂ (la tensione nella fune a 60 gradi), procedi in questo modo:
  - Secondo le leggi della trigonometria, il rapporto fra T = m(g) e T₁ o T₂equivale al coseno dell'angolo fra ciascuna corda e il soffitto. Per T₁, cos(30) = 0,87, mentre per T₂, cos(60) = 0,5
  - Moltiplica la tensione nella corda più in basso (T = mg) per il coseno di ciascun angolo per trovare T₁ e T₂.
  - T₁ = ,87 × m(g) = ,87 × 10(9,8) = 85,26 Newton.
  - T₂ = ,5 × m(g) = ,5 × 10(9,8) = 49 Newton.
Pubblicità