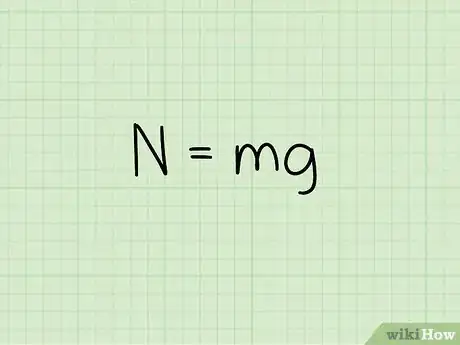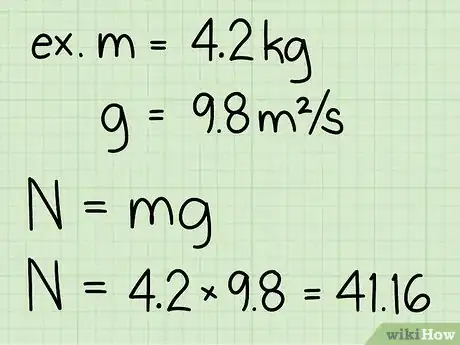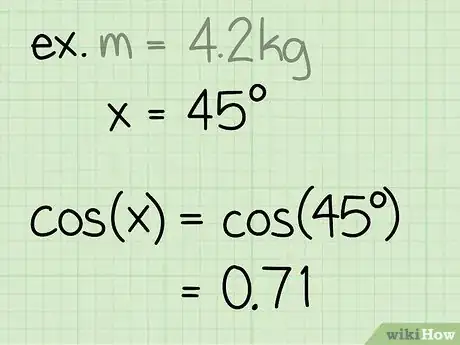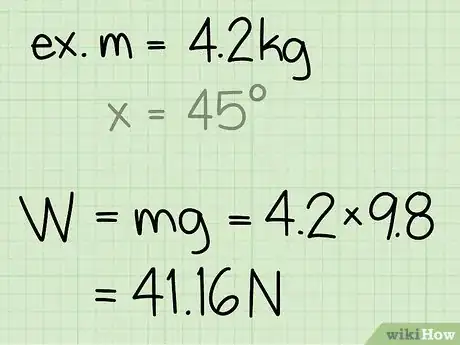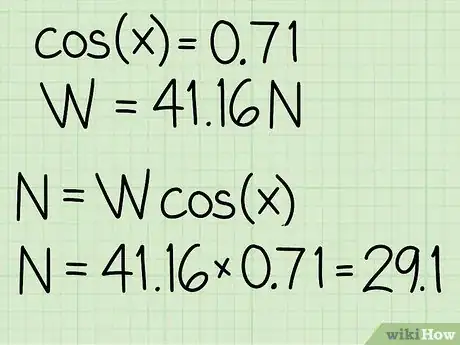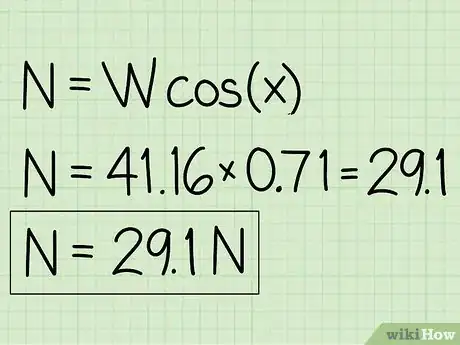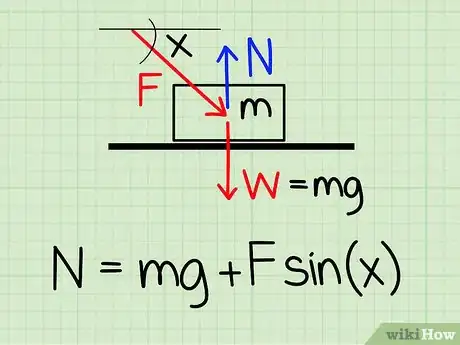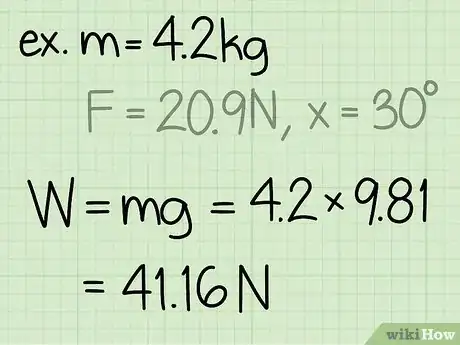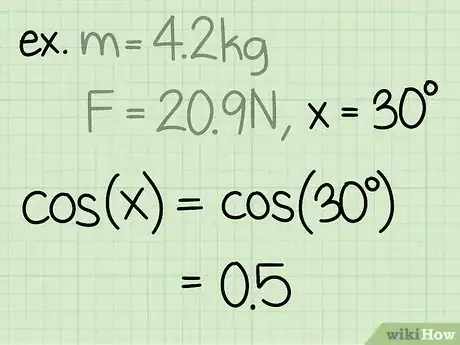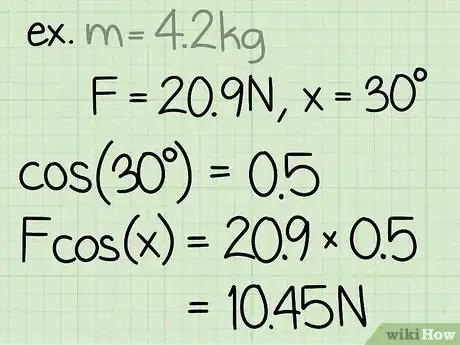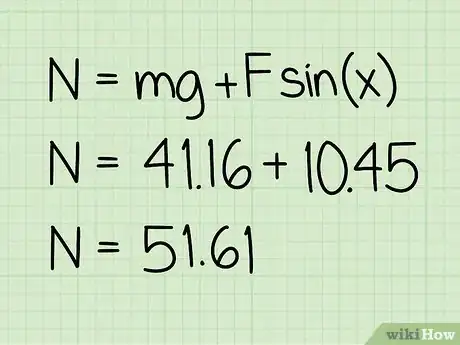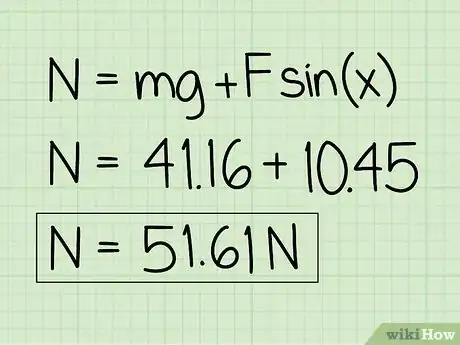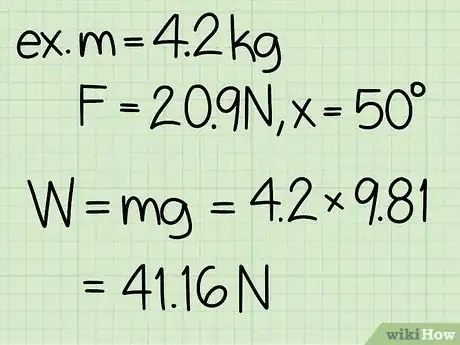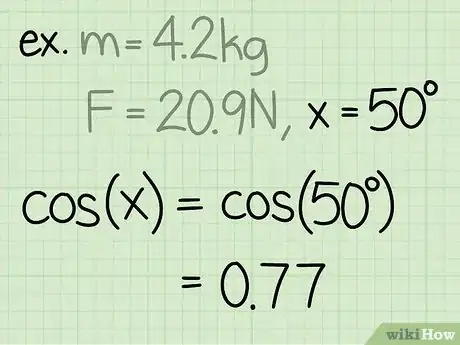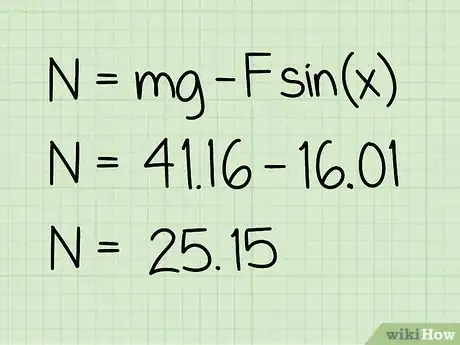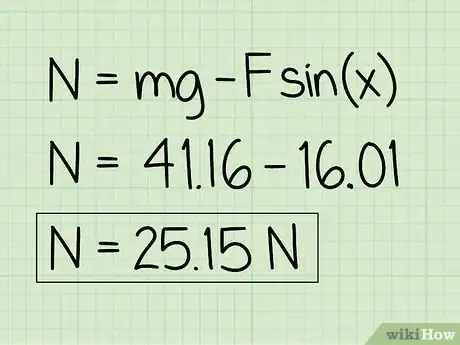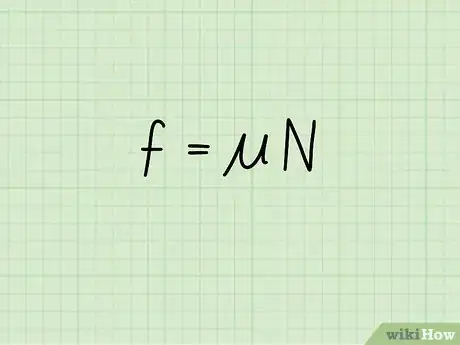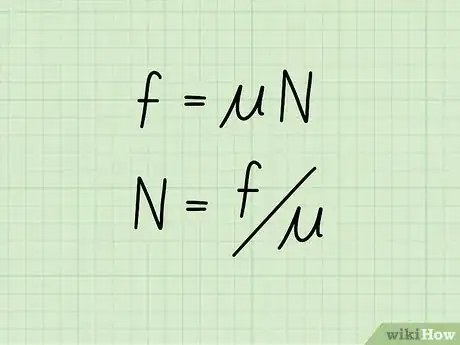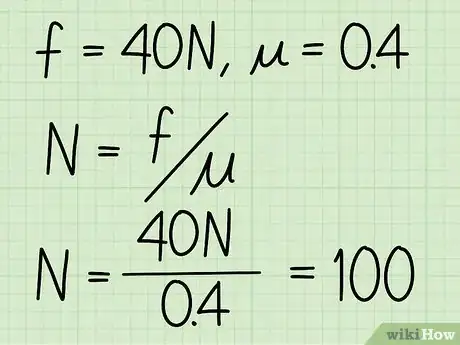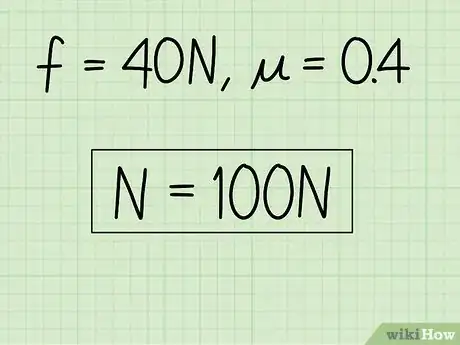Come Calcolare la Forza Normale

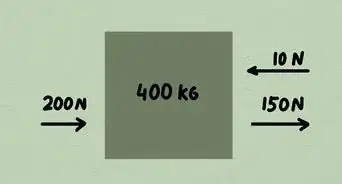
La forza normale è la quantità di forza necessaria a contrastare l'azione di forze esterne presenti in un dato scenario. Per calcolare la forza normale bisogna considerare le circostanze dell'oggetto e i dati a disposizione per le variabili. Continua a leggere per ulteriori informazioni.

Metodo 1
Metodo 1 di 5:

Forza Normale in Condizioni di Riposo

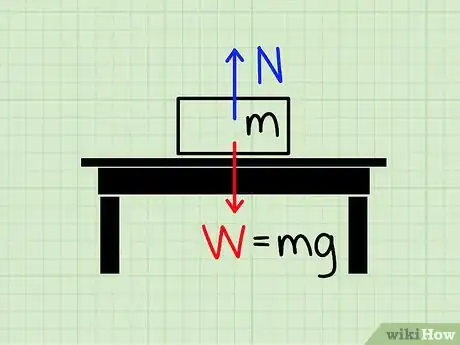
  1. Immagine titolata Find Normal Force Step 1
    1
    Comprendi il concetto di "forza normale". La forza normale si riferisce alla quantità di forza necessaria a contrastare la forza di gravità.
    • Immagina un blocco su un tavolo. La forza di gravità attira il blocco verso terra, ma esiste chiaramente un'altra forza all'opera che impedisce al blocco di attraversare il tavolo e schiantare al suolo. La forza che impedisce al blocco di cadere a dispetto della forza di gravità è, appunto, la forza normale.
  2. Immagine titolata Find Normal Force Step 2
    2
    Conosci l'equazione per calcolare la forza normale di un oggetto a riposo. Per calcolare la forza normale di un oggetto a riposo su una superficie piana, usa la formula: N = m * g[1]
    • In questa equazione, N si riferisce alla forza normale, m alla massa dell'oggetto, e g all'accelerazione di gravità.
    • Per un oggetto che si trova in condizione di riposo su una superficie piana, e non soggetta all'influenze di forze esterne, la forza normale è uguale al peso dell'oggetto. Al fine di mantenere fermo l'oggetto, la forza normale deve essere uguale alla forza di gravità che agisce sull'oggetto. La forza di gravità che agisce sull'oggetto è rappresentata dal peso dell'oggetto stesso, o la sua massa moltiplicata per l'accelerazione di gravità.
    • "Esempio": Calcola la forza normale di un blocco con una massa di 4,2 g.
  3. Immagine titolata Find Normal Force Step 3
    3
    Moltiplica la massa dell'oggetto per l'accelerazione di gravità. Il risultato ti darà il peso dell'oggetto, che equivale, in ultima analisi, alla forza normale dell'oggetto in condizione di riposo.
    • Nota che l'accelerazione gravitazionale sulla superficie della Terra è una costante: g = 9,8 m/s2[2]
    • "Esempio": peso = m * g = 4,2 * 9,8 = 41,16
  4. Immagine titolata Find Normal Force Step 4
    4
    Scrivi la tua risposta. Il passaggio precedente dovrebbe risolvere il problema fornendoti la risposta.
    • "Esempio": La forza normale è pari a 41,16 N.
    Pubblicità
Metodo 2
Metodo 2 di 5:

Forza Normale su un Piano Inclinato

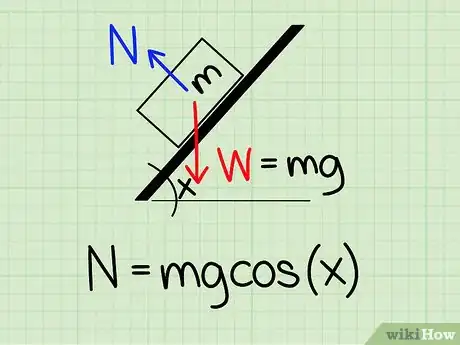
  1. Immagine titolata Find Normal Force Step 5
    1
    Usa l'equazione appropriata. Per calcolare la forza normale di un oggetto su un piano inclinato, bisogna usare la formula: N = m * g * cos(x)[3]
    • In questa equazione, N si riferisce alla forza normale, m alla massa dell'oggetto, g all'accelerazione di gravità, e x all'angolo di inclinazione.
    • "Esempio": Calcola la forza normale di un blocco con una massa di 4,2 g che si trova su una rampa con una pendenza di 45°.
  2. Immagine titolata Find Normal Force Step 6
    2
    Calcola il coseno dell'angolo. Il coseno di un angolo è uguale al seno dell'angolo complementare, o al lato adiacente diviso per l'ipotenusa del triangolo formato dalla pendenza[4]
    • Questo valore viene spesso calcolato tramite l'uso di una calcolatrice, dal momento che il coseno di un angolo è una costante, ma puoi anche calcolarlo manualmente.
    • "Esempio": cos(45) = 0,71
  3. Immagine titolata Find Normal Force Step 7
    3
    Trova il peso dell'oggetto. Il peso di un oggetto è uguale alla massa dell'oggetto moltiplicata per l'accelerazione di gravità.
    • Nota che l'accelerazione gravitazionale sulla superficie della Terra è una costante: g = 9,8 m/s2.
    • "Esempio": peso = m * g = 4,2 * 9,8 = 41,16
  4. Immagine titolata Find Normal Force Step 8
    4
    Moltiplica i due valori tra loro. Al fine di calcolare la forza normale, occorre moltiplicare il peso dell'oggetto per il coseno dell'angolo di inclinazione.
    • "Esempio": N = m * g * cos(x) = 41,16 * 0,71 = 29,1
  5. Immagine titolata Find Normal Force Step 9
    5
    Scrivi la tua risposta. Il passaggio precedente dovrebbe risolvere il problema e fornirti la risposta.
    • Nota che per un oggetto che si trova su un piano inclinato, la forza normale dovrebbe essere inferiore al peso dell'oggetto.
    • "Esempio"': La forza normale è pari a 29,1 N.
    Pubblicità
Metodo 3
Metodo 3 di 5:

Forza Normale in Casi di Pressione Esterna Verso il Basso

  1. Immagine titolata Find Normal Force Step 10
    1
    Usa l'equazione appropriata. Per calcolare la forza normale di un oggetto a riposo quando una forza esterna esercita su di esso una pressione verso il basso, usa l'equazione: N = m * g + F * sin(x).
    • N si riferisce alla forza normale, m alla massa dell'oggetto, g all'accelerazione di gravità, F alla forza esterna, e x all'angolo tra l'oggetto e la direzione della forza esterna.
    • "Esempio": Calcola la forza normale di un blocco con una massa di 4,2 g, quando una persona esercita sul blocco una pressione verso il basso a un angolo di 30° con una forza pari a 20,9 N.
  2. Immagine titolata Find Normal Force Step 11
    2
    Calcola il peso dell'oggetto. Il peso di un oggetto è uguale alla massa dell'oggetto moltiplicata per l'accelerazione di gravità.
    • Nota che l'accelerazione gravitazionale sulla superficie della Terra è una costante: g = 9,8 m/s2.
    • "Esempio": peso = m * g = 4,2 * 9,8 = 41,16
  3. Immagine titolata Find Normal Force Step 12
    3
    Trova il seno dell'angolo. Il seno di un angolo viene calcolato dividendo il lato del triangolo opposto all'angolo stesso per l'ipotenusa dell'angolo.
    • "Esempio": sin(30) = 0,5
  4. Immagine titolata Find Normal Force Step 13
    4
    Moltiplica il seno per la forza esterna. In questo caso, la forza esterna si riferisce alla pressione esercitata verso il basso sull'oggetto.
    • "Esempio": 0,5 * 20,9 = 10,45
  5. Immagine titolata Find Normal Force Step 14
    5
    Aggiungi questo valore al peso dell'oggetto. In questo modo otterrai il valore della forza normale.
    • "Esempio": 10,45 + 41,16 = 51,61
  6. Immagine titolata Find Normal Force Step 15
    6
    Scrivi la tua risposta. Nota che per un oggetto a riposo su cui viene esercitata una pressione esterna verso il basso, la forza normale sarà maggiore del peso dell'oggetto.
    • "Esempio": La forza normale è pari a 51,61 N.
    Pubblicità
Metodo 4
Metodo 4 di 5:

Forza Normale in Casi di Forza Esterna Diretta Verso l'Alto

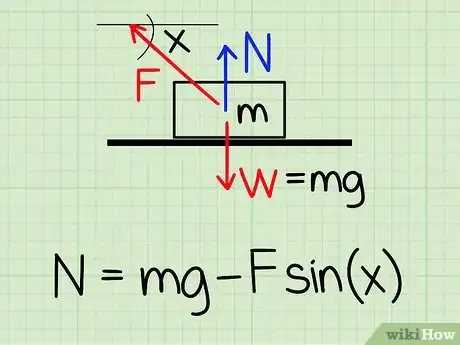
  1. Immagine titolata Find Normal Force Step 16
    1
    Usa l'equazione appropriata. Per calcolare la forza normale di un oggetto a riposo quando una forza esterna agisce sull'oggetto verso l'alto, usa l'equazione: N = m * g - F * sin (x).
    • N si riferisce alla forza normale, m alla massa dell'oggetto, g all'accelerazione di gravità, F alla forza esterna, e x all'angolo tra l'oggetto e la direzione della forza esterna.
    • "Esempio": Calcola la forza normale di un blocco con una massa di 4,2 g quando una persona tira il blocco verso l'alto a un angolo di 50° e con una forza pari a 20,9 N.
  2. Immagine titolata Find Normal Force Step 17
    2
    Trova il peso dell'oggetto. Il peso di un oggetto è uguale alla massa dell'oggetto moltiplicata per l'accelerazione di gravità.
    • Nota che l'accelerazione gravitazionale sulla superficie della Terra è una costante: g = 9,8 m/s2.
    • "Esempio": peso = m * g = 4,2 * 9,8 = 41,16
  3. Immagine titolata Find Normal Force Step 18
    3
    Calcola il seno dell'angolo. Il seno di un angolo viene calcolato dividendo il lato del triangolo opposto all'angolo stesso per l'ipotenusa dell'angolo.
    • "Esempio": sin(50) = 0,77
  4. Immagine titolata Find Normal Force Step 19
    4
    Moltiplica il seno per la forza esterna. In questo caso, la forza esterna si riferisce alla forza esercitata sull'oggetto verso l'alto.
    • "Esempio": 0,77 * 20,9 = 16,01
  5. Immagine titolata Find Normal Force Step 20
    5
    Sottrai questo valore dal peso. In questo modo otterrai la forza normale dell'oggetto.
    • "Esempio": 41,16 - 16,01 = 25,15
  6. Immagine titolata Find Normal Force Step 21
    6
    Scrivi la tua risposta. Nota che per un oggetto a riposo su cui agisce una forza esterna verso l'alto, la forza normale sarà inferiore al peso dell'oggetto.
    • "Esempio": La forza normale è pari a 25,15 N.
    Pubblicità
Metodo 5
Metodo 5 di 5:

Forza Normale e Attrito

  1. Immagine titolata Find Normal Force Step 22
    1
    Conosci l'equazione di base per calcolare l'attrito cinetico. L'attrito cinetico, o l'attrito di un oggetto in movimento, è pari al coefficiente di attrito moltiplicato per la forza normale di un oggetto. L'equazione si presenta nella seguente forma: f = μ * N
    • In questa equazione, f si riferisce all'attrito, μ al coefficiente di attrito, e N alla forza normale dell'oggetto.
    • Il "coefficiente di attrito" è il rapporto tra la resistenza di attrito e la forza normale, ed è responsabile per la pressione esercitata su entrambi le superfici contrapposte.
  2. Immagine titolata Find Normal Force Step 23
    2
    Riorganizza l'equazione per isolare la forza normale. Se disponi di un valore per l'attrito cinetico di un oggetto, e del coefficiente di attrito di quell'oggetto, puoi calcolare la forza normale usando la formula: N = f / μ
    • Entrambi i lati dell'equazione originale sono stati divisi per μ, isolando così da un lato la forza normale, e dall'altro il coefficiente di attrito e l'attrito cinetico.
    • "Esempio": Calcola la forza normale di un blocco quando il coefficiente di attrito è di 0,4 e la quantità di attrito cinetico di 40 N.
  3. Immagine titolata Find Normal Force Step 24
    3
    Dividi l'attrito cinetico per il coefficiente di attrito. Questo è in sostanza tutto ciò che bisogna fare per calcolare il valore della forza normale.
    • "Esempio": N = f / μ = 40 / 0,4 = 100
  4. Immagine titolata Find Normal Force Step 25
    4
    Scrivi la tua risposta. Se lo reputi necessario, puoi controllare la tua risposta inserendola nuovamente nell'equazione originale per l'attrito cinetico. In caso contrario, avrai risolto il problema.
    • "Esempio": La forza normale è pari a 100 N.
    Pubblicità

Cose che ti Serviranno

  • Penna
  • Carta
  • Calcolatrice

wikiHow Correlati

Calcolare il Baricentro
Come
Calcolare il Baricentro
Calcolare l'Accelerazione
Come
Calcolare l'Accelerazione
Calcolare l'Accelerazione Angolare
Come
Calcolare l'Accelerazione Angolare
Calcolare la Forza di Gravità
Come
Calcolare la Forza di Gravità
Calcolare la Forza
Come
Calcolare la Forza
Calcolare la Tensione in Fisica
Come
Calcolare la Tensione in Fisica
Calcolare la Potenza Elettrica
Come
Calcolare la Potenza Elettrica
Calcolare Resistenze in Serie e in Parallelo
Come
Calcolare Resistenze in Serie e in Parallelo
Calcolare l'Impedenza
Come
Calcolare l'Impedenza
Calcolare la Frequenza
Come
Calcolare la Frequenza
Calcolare la Lunghezza d'Onda
Come
Calcolare la Lunghezza d'Onda
Convertire i Watt in Ampere
Come
Convertire i Watt in Ampere
Pubblicità

Riferimenti

  1. ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/frict.html
  2. ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/mass.html#wgt
  3. ↑ http://www.phy-astr.gsu.edu/butler/labs/physics1111/4NormalForce1111.pdf
  4. ↑ http://www.mathsisfun.com/sine-cosine-tangent.html

Informazioni su questo wikiHow

wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo. Questo articolo è stato visualizzato 126 380 volte
Categorie: Fisica
Pubblicità