Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 436 879 volte
Saper convertire i numeri in percentuali, frazioni e decimali è una delle abilità matematiche basilari che è fondamentale acquisire. Una volta appreso, il concetto alla base del processo di conversione diverrà facile da padroneggiare e utilizzare. Imparare a convertire rapidamente le piccole cifre di uso quotidiano ti sarà di grande aiuto sia nei test scolastici sia nei calcoli in ambito finanziario.
Passaggi
Convertire le Percentuali
-
1Per convertire una percentuale in un numero decimale, sposta il separatore (la virgola) di due posizioni verso sinistra. A meno di altre indicazioni, una percentuale presenta il separatore decimale dopo l'ultimo numero. Per esempio, la percentuale 75% può essere espressa correttamente anche nella forma 75,0%. Spostando il separatore decimale di due posizioni verso sinistra si ottiene la conversione della percentuale in un numero decimale. Si tratta dello stesso risultato che si ottiene dividendo lo stesso numero per 100. Ecco alcuni esempi:[1]
- 75% convertito in numero decimale diventa 0,75;
- 3,1% convertito in numero decimale diventa 0,031;
- 0,5% convertito in numero decimale diventa 0,005.
-
2Esprimi una percentuale come una frazione del numero 100. Si tratta di un altro modo corretto per esprimere un numero percentuale. Il coefficiente della percentuale viene trasformato nel numeratore della frazione, mentre 100 diviene il denominatore. A questo punto, ove possibile, procedi semplificando la frazione ottenuta nei minimi termini.
- Esempio: la percentuale 36% può essere scritta come 36/100.
- Per eseguire la semplificazione dei termini della frazione, occorre individuare il massimo comune divisore, cioè il numero più grande in grado di dividere numeratore e denominatore della frazione (36 e 100). In questo caso si tratta del numero 4.
- Eseguendo i calcoli il risultato che otterremo sarà 9/25.
- Per controllare se il risultato ottenuto è corretto, dividi il numeratore della frazione per il denominatore (9 / 25 = 0,36), quindi moltiplica il dividendo ottenuto per 100 (36%). Il numero finale dovrebbe coincidere con il coefficiente della percentuale iniziale.
-
3Elimina il simbolo di percentuale. Dopo che la percentuale originale è stata convertita in un numero decimale o in una frazione, il simbolo % non va più indicato. Ricorda che una percentuale indica una parte dell'insieme totale che è rappresentato dal numero 100. Quindi, se al termine della conversione non rimuovi il simbolo %, la tua soluzione al problema non è corretta.[2]Pubblicità
Convertire i Numeri Decimali
-
1Per convertire un numero decimale in una percentuale, moltiplicalo per il coefficiente 100. In altre parole, sposta il separatore decimale (la virgola) di due posizioni verso destra. Il simbolo percentuale tradotto in parole significa letteralmente "per cento", quindi, dopo essere stato moltiplicato per cento, un numero decimale diviene una percentuale.[3] Ecco alcuni esempi: 0,32 espresso in percentuale diventa 32%; 0,07 espresso in percentuale diventa 7%; 1,25 espresso in percentuale diventa 125%; 0,083 espresso in percentuale diventa 8,3%.
-
2Converti un numero decimale limitato in una frazione. Un numero decimale si dice limitato quando è composto da un numero finito di cifre decimali. Sposta il separatore decimale, cioè la virgola, verso destra per il numero di cifre decimali presenti. Il numero ottenuto rappresenta il numeratore della nostra frazione. Il denominatore è rappresentato dal numero 1 seguito da tanti 0 quante erano le cifre decimali del numero originale. Come ultimo passaggio semplifichiamo ai minimi termini la frazione ottenuta.[4]
- Per esempio: il numero 0,32 presenta due cifre decimali, quindi spostiamo il separatore decimale verso destra di due posizioni e dividiamo il risultato per 100 ottenendo la frazione 32/100. Avendo un massimo comune divisore pari a 4, la frazione risultante dal passaggio precedente può essere semplificata nella forma 8/25.
- Ecco un altro esempio: il numero 0,8 presenta una sola cifra decimale, quindi, spostando il separatore decimale verso destra di una posizione e dividendo il risultato per 10, otterremo la seguente frazione 8/10. Semplificando il risultato utilizzando il massimo comune divisore 2 otterremo la frazione 4/5.
- Per verificare la correttezza del tuo lavoro, devi semplicemente calcolare il risultato della frazione, assicurandoti che sia identico al numero decimale di partenza. Nel nostro esempio otteniamo 8 / 25 = 0,32.
-
3Converti un numero decimale periodico in una frazione. Un numero decimale periodico è un numero composto da infinite cifre decimali che si ripetono con regolarità. Ad esempio, il numero decimale 0,131313... è composto da due cifre (1 e 3) che si ripetono all'infinito. Determina il numero di cifre che compongono il "periodo" del numero in esame (cioè le cifre decimali che si ripetono all'infinito), quindi moltiplica l'intero numero per 10n, dove "n" rappresenta il numero di cifre che compongono il periodo.[5]
- Ad esempio: 0,131313... deve essere moltiplicato per 100 (risultato di 102) ottenendo così 13,131313... .
- Per determinare il numeratore della nostra frazione occorre sottrarre la parte decimale al numero ottenuto nel passaggio precedente. Nel nostro esempio avremo 13,131313... - 0,131313... = 13.[6]
- Per determinare il denominatore, si deve sottrarre 1 alla potenza di 10 utilizzata nel primo passaggio della conversione. Nel nostro esempio 0,131313... è stato moltiplicato per 100, quindi il denominatore sarà 100 - 1 = 99.
- Al termine della conversione, possiamo scrivere che il numero decimale periodico 0,131313… in forma frazionaria si esprime come 13/99.
- Ecco altri esempi:
- 0,333... è rappresentato dalla frazione 3/9;
- 0,123123123... è rappresentato dalla frazione 123/999;
- 0,142857142857... è rappresentato dalla frazione 142857/999999.
- Se necessario, è possibile semplificare ai minimi termini la frazione risultante dalla conversione. Ad esempio, semplificando la frazione 142857/999999 si ottiene 1/7.
Pubblicità
Convertire le Frazioni
-
1Per convertire una frazione in un numero decimale, dividi semplicemente il numeratore per il denominatore. Interpreta il simbolo di frazione come il dover eseguire una divisione. Questo significa che qualsiasi frazione nella forma "x / y" può essere descritta come "x diviso y".[7]
- Ad esempio: la frazione 4/8 dà come risultato il numero decimale 0,5.
-
2Determina come arrotondare il numero decimale risultante dalla conversione. Molte frazioni non danno come risultato un numero intero, in tal caso occorre quindi valutare a che decimale arrotondare il risultato finale della divisione. La convenzione adottata con maggior frequenza prevede di utilizzare 2 decimali. Ricorda la regola base per eseguire l'arrotondamento di un numero decimale troncato: se il primo numero troncato è 5 occorre arrotondare la cifra precedente al decimale superiore. Ad esempio, il numero decimale 0,145 va arrotondato a 0,15.
- Ad esempio: la frazione 5/17 dà come risultato il numero decimale 0,2941176470588… ;
- Il risultato finale arrotondato risulterà essere semplicemente 0,29.
-
3Per convertire una frazione in una percentuale occorre eseguire la divisione e moltiplicare il risultato ottenuto per 100. Partiamo procedendo esattamente come nella conversione di una frazione in un numero decimale, quindi dividiamo il numeratore per il denominatore. A questo punto moltiplichiamo il risultato ottenuto per 100 e completiamo la conversione aggiungendo il simbolo di %.[8]
- Ad esempio, procediamo alla conversione della frazione 4/8 dividendo 4 per 8, ottenendo così 0,50. A questo punto moltiplichiamo il risultato per 100 ottenendo la risposta finale cioè 50%.
- Ecco altri esempi:
- 3/10 = 0,30 * 100 = 30%;
- 5/8 = 0,625 * 100 = 62,5%.
Pubblicità
Consigli
- Una conoscenza eccellente delle tabelle aritmetiche (tabelline) ti sarà di grande aiuto.
- Rispetta l'opinione del professore o dell'insegnante in merito all'utilizzo della calcolatrice in classe. Se l'uso di tale strumento non è permesso o ben visto, è meglio non utilizzarlo.
- Molte calcolatrici sono dotate della funzione per il calcolo delle frazioni. In questo caso potrebbe essere utile usare la calcolatrice per ridurre una frazione ai minimi termini. Per avere maggiori dettagli in merito alla procedura da seguire, consulta il manuale di istruzioni del dispositivo.
Avvertenze
- Assicurati che il separatore decimale (la virgola) sia inserito nella posizione corretta.
- Quando converti una frazione in un numero decimale, assicurati di dividere il numeratore per il denominatore.
Cose che ti Serviranno
- Foglio di carta e matita
- Calcolatrice
Riferimenti
- ↑ https://www.mathsisfun.com/converting-percents-decimals.html
- ↑ https://www.mathsisfun.com/converting-percents-decimals.html
- ↑ http://www.mathsisfun.com/converting-decimals-percents.html
- ↑ https://www.mathsisfun.com/converting-decimals-fractions.html
- ↑ http://www.basic-mathematics.com/converting-repeating-decimals-to-fractions.html
- ↑ http://www.virtualnerd.com/pre-algebra/rational-numbers/definitions-basics/convert-decimals-fractions/repeating-decimal-to-fraction-conversion
- ↑ https://www.mathsisfun.com/converting-fractions-decimals.html
- ↑ https://www.mathsisfun.com/converting-fractions-percents.html


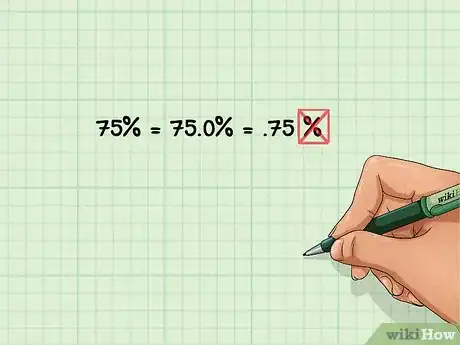


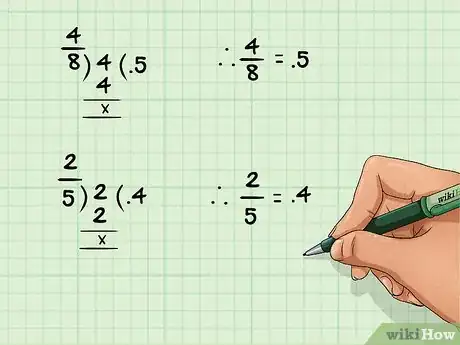

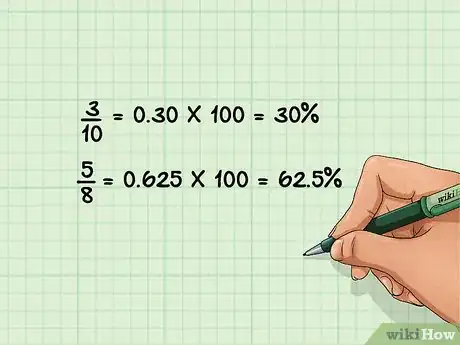




-to-Grams-(g)-Step-12-Version-4.webp)













Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 436 879 volte