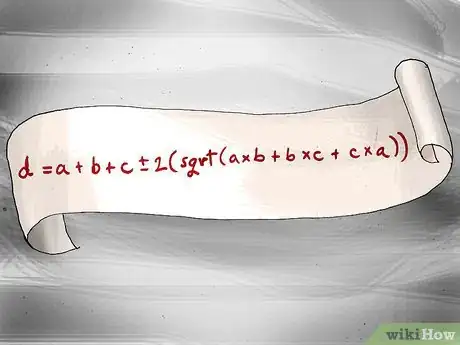Come Creare una Guarnizione Apollinea

Info sull'Autore

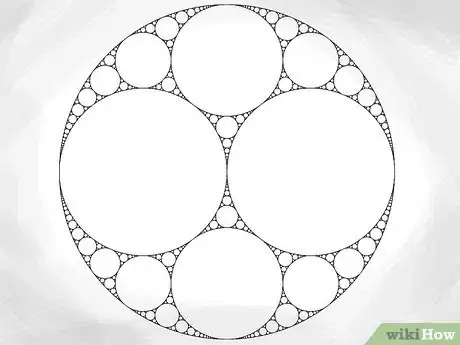
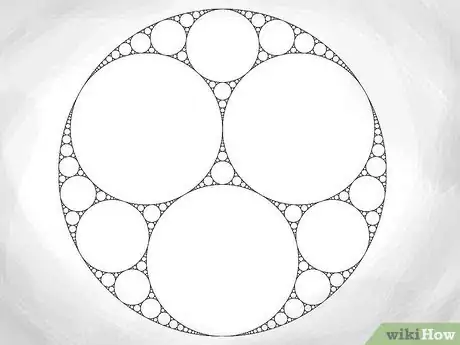
Una Guarnizione Apollinea è un tipo di immagine frattale, formata da cerchi che diventano via via più piccoli contenuti in un unico grande cerchio. Ogni cerchio nella Guarnizione Apollinea è "tangente" ai cerchi adiacenti - in altre parole, questi cerchi si toccano in punti infinitamente piccoli. Chiamata Guarnizione Apollinea in onore del matematico Apollonio di Perga, questo tipo di frattale può essere portato a un ragionevole livello di complessità (a mano o con il computer) e forma un'immagine meravigliosa e impressionante. Leggi il Passaggio 1 per iniziare.

Parte 1

Parte 1 di 2:

Comprendere i Concetti Chiave

"Per essere chiari: se sei semplicemente interessato a "disegnare" una Guarnizione Apollinea, non è necessario cercare i principi matematici che si celano dietro al frattale. Tuttavia, nel caso volessi comprendere a fondo la Guarnizione Apollinea, è importante che tu comprenda la definizione di diversi concetti che useremo nella discussione".

1
Definisci i termini chiave. I seguenti termini sono utilizzati nelle istruzioni più in basso:
- Guarnizione Apollinea: uno dei diversi nomi che si applicano ad un tipo di frattale composto da una serie di cerchi annidati dentro un grande cerchio e tangenti l'uno all'altro. Questi sono anche chiamati "Cerchi a Zolle" o "Cerchi Bacianti".
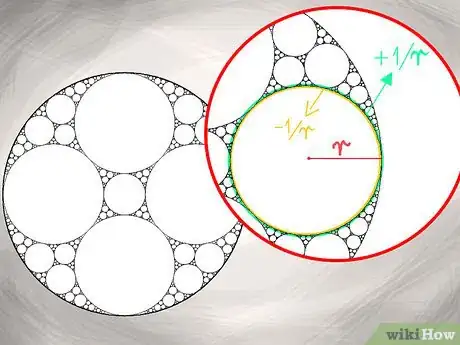
- Raggio di un cerchio: la distanza tra il punto centrale di un cerchio e la sua circonferenza, a cui di solito si assegna la variabile "r".
- Curvatura di un cerchio: la funzione, positiva o negativa, inversa al raggio, o ±1/r. La curvatura è positiva quando si calcola la curvatura esterna, negativa quando si calcola quella interna.
- Tangente: un termine applicato a linee, piani e forme che si intersecano in un punto infinitesimale. Nelle Guarnizioni Apollinee, questo si riferisce al fatto che ogni cerchio tocca tutti i cerchi vicini in un solo punto. Nota che non ci sono intersezioni - le forme tangenti non si sovrappongono.
2
Comprendi il Teorema di Cartesio. Il teorema di Cartesio è una formula utile per calcolare le dimensioni dei cerchi nella Guarnizione Apollinea. Se definiamo le curvature (1/r) di tre cerchi qualsiasi - rispettivamente "a", "b" e "c" - la curvatura del cerchio tangente a tutti e tre (che chiameremo "d") è: d = a + b + c ± 2 (sqrt (a × b + b × c + c × a )).
- Per i nostri scopi, in genere useremo solo la risposta che otterremo mettendo un segno '+' di fronte alla radice quadrata (in altre parole, ... + 2 (sqrt(...)). Per ora è sufficiente sapere che l'equazione di forma negativa ha la sua utilità in altri contesti.
Pubblicità

Parte 2

Parte 2 di 2:

Costruire la Guarnizione Apollinea

"Le Guarnizioni Apollinee hanno la forma di magnifici arrangiamenti frattali di cerchi che vanno via via rimpicciolendosi. Matematicamente, le Guarnizioni Apollinee sono infinitamente complesse, ma, sia usando un programma di disegno, sia disegnando a mano, potrai arrivare a un punto in cui sarà impossibile disegnare cerchi più piccoli. Più precisi sono i cerchi, più sarai in grado di riempire a guarnizione".

1
Prepara i tuoi strumenti da disegno, analogici o digitali che siano. Nei passaggi qua sotto, faremo una Guarnizione Apollinea semplice. È possibile disegnare una Guarnizione Apollinea a mano o al computer. In entrambi i casi, sforzati di disegnare dei cerchi perfetti. È piuttosto importante perché ogni cerchio nella Guarnizione Apollinea è perfettamente tangente ai cerchi che gli sono vicini; cerchi che siano anche solo lievemente irregolari possono rovinare il tuo prodotto finale.
- Se stai disegnando al computer, avrai bisogno di un programma che ti permetta di disegnare con facilità cerchi con raggio fisso dal punto centrale. Puoi usare Gfig, un'estensione che disegna vettorialmente per GIMP, un programma gratuito di modifica delle immagini, così come una miriade di altri programmi di disegno (guarda la sezione dei materiali per alcuni link utili). Probabilmente avrai bisogno anche di una calcolatrice e di qualcosa su cui annotare raggi e curvature.
- Per disegnare a mano la Guarnizione avrai bisogno di una calcolatrice scientifica, una matita, un compasso, un righello (preferibilmente con scala al millimetro), della carta e un block notes.
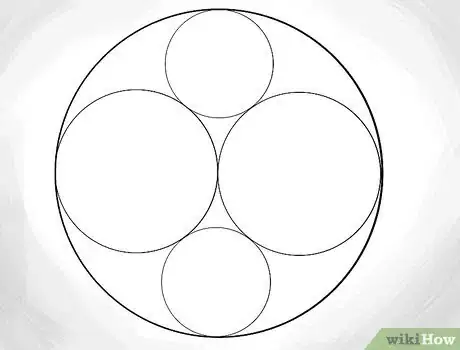
2
Inizia con un grande cerchio. Il primo compito è facile - disegna semplicemente un grande cerchio che sia perfettamente tondo. Più grande è il cerchio, più complessa sarà la guarnizione, perciò cerca di disegnare un cerchio tanto grande quanto la pagina su cui stai disegnando.
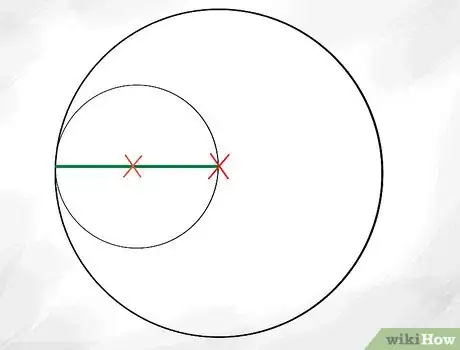
3
Disegna un cerchio più piccolo dentro quello originale, tangente a un lato. Poi disegna un altro cerchio dentro quello più piccolo. Le dimensioni del secondo cerchio dipendono da te - non ci sono dimensioni esatte. Comunque, per i nostri scopi, disegniamo il secondo cerchio in modo che il suo punto centrale sia a metà del raggio del cerchio più grande.
- Ricorda che nelle Guarnizioni Apollinee, tutti i cerchi che si toccano sono tangenti l'uno all'altro. Se stai usando un compasso per disegnare i tuoi cerchi a mano, ricrea questo effetto mettendo la punta del compasso a metà del raggio del cerchio esterno più grande, aggiustando poi la matita in modo che "sfiori" appena il bordo del cerchio grande e, infine, disegnando il cerchio più piccolo.
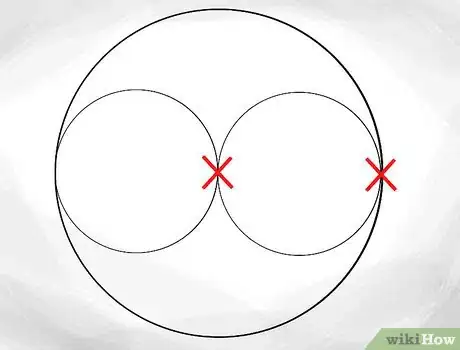
4
Disegna un cerchio identico che attraversi il cerchio più piccolo all'interno. In seguito, disegniamo un altro cerchio che attraversi il primo. Questo cerchio dovrebbe essere tangente sia al cerchio più esterno sia a quello più interno; questo significa che i due cerchi interni si toccheranno esattamente a metà di quello più grande.
5
Applica il Teorema di Cartesio per scoprire le dimensioni dei prossimi cerchi. Smetti di disegnare per un attimo. Ricorda che il Teorema di Cartesio è d = a + b + c ± 2 (sqrt (a × b + b × c + c × a )), dove a, b e c sono le curvature dei tuoi tre cerchi tangenti. Perciò, per trovare il raggio del prossimo cerchio, troviamo prima la curvatura di ognuno dei tre cerchi che già abbiamo disegnato in modo da poter trovare la curvatura del prossimo cerchio, per poi convertirla e trovare il raggio.
- Definiamo il raggio del cerchio più esterno come 1. Poiché gli altri cerchi sono dentro quest'ultimo, ne stiamo trattando la curvatura "interna" (piuttosto che quella esterna), e, di conseguenza, sappiamo che la sua curvatura è negativa. - 1/r = -1/1 = -1. La curvatura del cerchio grande è -1.
- I raggi dei cerchi più piccoli sono lunghi la metà di quello grande, o, in altre parole, 1/2. Dato che questi cerchi toccano il cerchio più grande e si toccano tra di loro, stiamo trattando la loro curvatura "esterna", sicché le curvature sono positive. 1/(1/2) = 2. Le curvature dei cerchi più piccoli sono entrambe 2.
- Ora, sappiamo che a = -1, b = 2, and c = 2 secondo l'equazione del Teorema di Cartesio. Risolviamo d:
  - d = a + b + c ± 2 (sqrt (a × b + b × c + c × a ))
  - d = -1 + 2 + 2 ± 2 (sqrt (-1 × 2 + 2 × 2 + 2 × -1 ))
  - d = -1 + 2 + 2 ± 2 (sqrt (-2 + 4 + -2 ))
  - d = -1 + 2 + 2 ± 0
  - d = -1 + 2 + 2
  - d = 3. La curvatura del prossimo cerchio sarà 3. Poiché 3=1/r, il raggio del prossimo cerchio è 1/3.
6
Crea il prossimo set di cerchi. Usa il valore del raggio che hai appena trovato per disegnare i prossimi due cerchi. Ricorda che questi saranno tangenti ai cerchi le cui curvature a, b e c sono state usate per il Teorema di Cartesio. In altre parole, saranno tangenti ai cerchi originali e ai secondi cerchi. Per rendere questi cerchi tangenti agli altri tre, dovrai disegnarli negli spazi vuoti dell'area del cerchio più grande.
- Ricorda che i raggi di questi cerchi saranno uguali a 1/3. Misura 1/3 sul bordo del cerchio più esterno, poi disegna il nuovo cerchio. Dovrebbe risultare tangente agli altri tre cerchi.
7
Continua ad aggiungere cerchi in questo modo. Siccome sono frattali, le Guarnizioni Apollinee sono infinitamente complesse. Questo significa che puoi aggiungerne sempre di più piccoli a seconda di ciò che vuoi. Sei limitato solo dalla precisione dei tuoi strumenti (o, se stai usando il computer, l'abilità dello zoom del tuo programma di disegno). Ogni cerchio, non importa quanto sia piccolo, dovrebbe essere tangente agli altri tre. Per disegnare i cerchi successivi, usa le curvature dei tre cerchi a cui saranno tangenti nel Teorema di Cartesio. Poi, usa la risposta (che sarà il raggio del nuovo cerchio) per disegnare accuratamente il nuovo cerchio.
- Nota che la Guarnizione che abbiamo deciso di disegnare è simmetrica, perciò il raggio di uno dei cerchi è lo stesso del cerchio corrispondente "che lo attraversa". Comunque, sappi che non tutte le Guarnizioni Apollinee sono simmetriche.
- Facciamo un altro esempio. Diciamo che, dopo aver disegnato l'ultima serie di cerchi, vogliamo disegnare dei cerchi che siano tangenti alla terza serie, alla seconda e al cerchio grande più esterno. Le curvature di questi cerchi sono rispettivamente 3, 2 e -1. Usiamo questi numeri nel Teorema di Cartesio, ponendo a = -1, b = 2, and c = 3:
  - d = a + b + c ± 2 (sqrt (a × b + b × c + c × a ))
  - d = -1 + 2 + 3 ± 2 (sqrt (-1 × 2 + 2 × 3 + 3 × -1 ))
  - d = -1 + 2 + 3 ± 2 (sqrt (-2 + 6 + -3))
  - d = -1 + 2 + 3 ± 2 (sqrt (1))
  - d = -1 + 2 + 3 ± 2
  - d = 2, 6. Abbiamo due risposte! Tuttavia, poiché sappiamo che il nostro nuovo cerchio sarà più piccolo di ogni cerchio a cui è tangente, solo una curvatura 6 (e quindi un raggio di 1/6) avrebbe senso.
  - L'altra risposta, 2, si riferisce attualmente al cerchio ipotetico sull'"altro lato" del punto tangente dei secondi e terzi cerchi. Questo "è" tangente sia a questi cerchi sia al cerchio più esterno, ma dovrebbe intersecare i cerchi già disegnati, perciò possiamo non considerarlo.
8
Come sfida, prova a fare una Guarnizione Apollinea non simmetrica cambiando le dimensioni del secondo cerchio. Tutte le Guarnizioni Apollinee iniziano allo stesso modo - con un largo cerchio esterno che funge da bordo del frattale. Tuttavia, non c'è motivo per cui il tuo secondo cerchio debba avere un raggio che sia metà del primo - l'abbiamo fatto così solo perché è semplice da capire. Per divertimento, inizia una nuova Guarnizione con un secondo cerchio di dimensioni differenti. Ciò ti porterà a nuove emozionanti strade d'esplorazione.
- Dopo aver disegnato il tuo secondo cerchio (senza riguardo per le dimensioni), la tua prossima mossa dovrebbe essere disegnare uno o più cerchi che siano tangenti sia a questo che al cerchio grande più esterno - non c'è un modo corretto. Dopodiché puoi usare il Teorema di Cartesio per determinare i raggi di ogni cerchio successivo, come mostrato sopra.
Pubblicità