X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 50 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 17 216 volte
I problemi sulle frazioni possono sembrare difficili, ma un po' di pratica e di conoscenza renderanno tutto più facile. Ecco come risolvere degli esercizi con le frazioni.
Passaggi
Metodo 1
Metodo 1 di 4:
Moltiplicare frazioni
-
1Hai bisogno di lavorare con due frazioni. Queste istruzioni funzionano solo nel caso di due frazioni. Se hai dei numeri misti, prima trasformali in frazioni improprie.
-
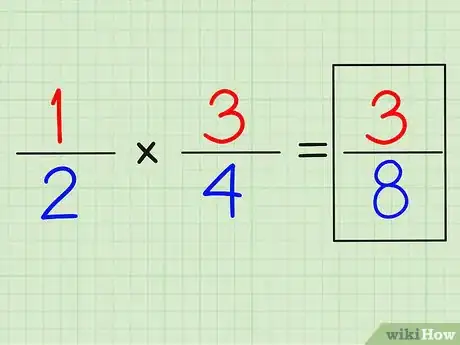
2Moltiplica numeratore x numeratore, quindi denominatore x denominatore.
- Avendo 1/2 x 3/4, moltiplica 1 x 3 e 2 x 4. La risposta è 3/8.
Pubblicità
Metodo 2
Metodo 2 di 4:
Dividere frazioni
-
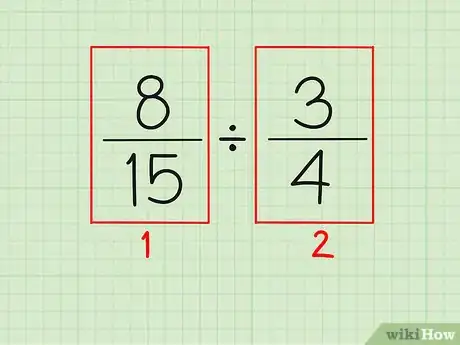
1Hai bisogno di lavorare con due frazioni. Di nuovo, la procedura funzionerà SOLO se hai già convertito eventuali numeri misti in frazioni improprie.
-
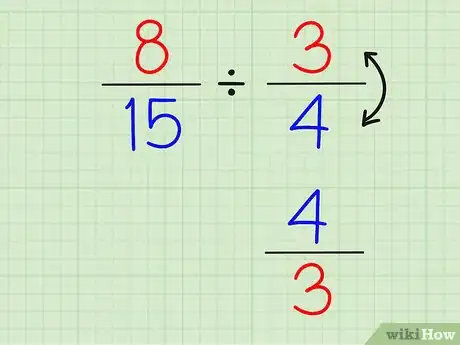
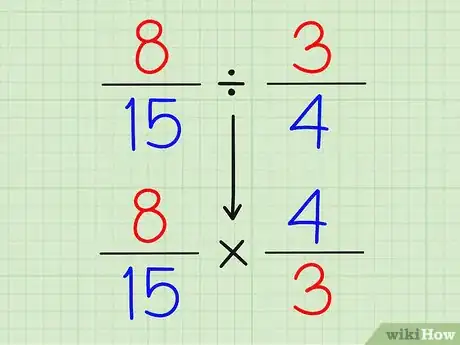
2Inverti la seconda frazione. Non importa quale frazione scegli come seconda.
-
3Cambia il segno della divisione nel segno della moltiplicazione.
- Se sei partito da 8/15 ÷ 3/4, allora diventerà 8/15 x 4/3
-
4Moltiplica sopra x sopra e sotto x sotto.
- 8 x 4 è 32 e 15 x 3 è 45, da cui il risultato è 32/45.
Pubblicità
Metodo 3
Metodo 3 di 4:
Convertire dei numeri misti in frazioni improprie
-
1Converti dei numeri misti in frazioni improprie. Le frazioni improprie sono delle frazioni in cui il numeratore è maggiore del denominatore. (Per esempio, 17/5.) Se stai moltiplicando o dividendo, prima di fare gli altri calcoli, devi convertire i numeri misti in frazioni improprie.
- Supponiamo che il numero misto sia 3 2/5 (tre e due quinti).
-
2
-
3Aggiungi il risultato al numeratore.
- Nel nostro caso, aggiungiamo 15 + 2 per avere 17
-
4Scrivi questa somma sopra il denominatore originale e otterrai una frazione impropria.
- Nel nostro caso, otterremo 17/5.
Pubblicità
Metodo 4
Metodo 4 di 4:
Sommare e sottrarre frazioni
-
1Trova il minimo comune denominatore (il numero in basso). Sia per l'addizione che per la sottrazione, si incomincia allo stesso modo. Trova la frazione comune più piccola che contenga entrambi i denominatori.
- Per esempio, tra 1/4 e 1/6, il minimo comune denominatore è 12. (4x3=12, 6x2=12)
-
2Moltiplica le frazioni per accordarsi con il minimo comune denominatore. Ricorda che nel fare ciò, non stai realmente cambiando il valore, ma solo i termini in cui è espresso. Pensa a una pizza: 1/2 di pizza e 2/4 di pizza sono la stessa quantità.
- Calcola quante volte il denominatore attuale è contenuto nel minimo comune denominatore. Per 1/4, 4 moltiplicato per 3 dà 12. Per 1/6, 6 moltiplicato per 2 dà 12.
- Moltiplica il numeratore e il denominatore della frazione per quel numero. Nel caso di 1/4, moltiplica sia 1 che 4 per 3, ottenendo 3/12. 1/6 moltiplicato per 2 dà 2/12. Ora il problema sarà: 3/12 + 2/12 o 3/12 - 2/12.
-
3Somma o sottrai i due numeratori (numeri in alto) ma NON i denominatori. Questo perché vuoi determinare quante sono in totale le frazioni di quel tipo. Se sommassi anche i denominatori, cambieresti il tipo di frazioni.
- Per 3/12 + 2/12, il risultato finale è 5/12. Per 3/12 - 2/12, è 1/12
Pubblicità
Consigli
- Per ottenere il reciproco di un numero intero, semplicemente scrivigli sopra un 1. Per esempio, 5 diventa 1/5.
- Un altro modo per dire "inverti la frazione" è dire "trova il reciproco". E' comunque lo stesso che scambiare il numeratore e il denominatore. Es. 2/4 sarà 4/2
- Le conoscenze elementari delle quattro operazioni (moltiplicazione, divisione, addizione e sottrazione) renderanno i calcoli facili e veloci.
- Puoi moltiplicare e dividere numeri misti senza convertirli prima in frazioni improprie. Ma questo coinvolge l'uso della proprietà distributiva in un metodo che può essere complesso. E' quindi meglio fare uso delle frazioni improprie.
- Quando scrivi il reciproco di un numero negativo, il segno non cambia.
Pubblicità
Avvertenze
- Converti i numeri misti in frazioni improprie prima di incominciare.
- Chiedi al tuo insegnante se devi dare i risultati nei minimi termini o no.
- Per esempio, 2/5 è il minimo termine, ma 16/40 non lo è.
- Chiedi al tuo insegnante se devi convertire i risultati in frazioni improprie in numeri misti.
- Per esempio, 3 1/4 invece di 13/4.
Pubblicità
Informazioni su questo wikiHow
Pubblicità



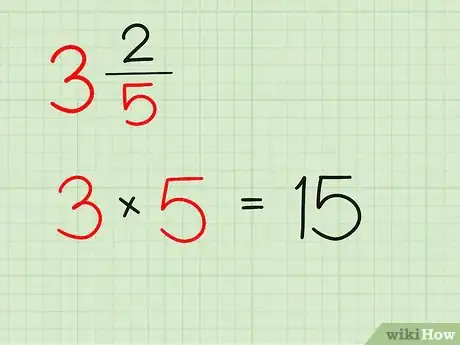
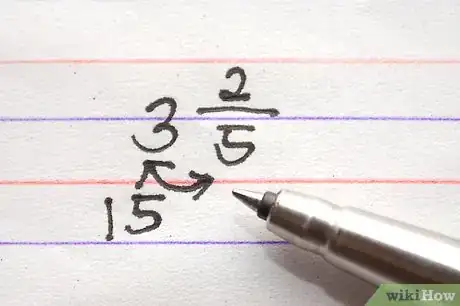








-to-Grams-(g)-Step-12-Version-4.webp)