wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 23 054 volte
Una funzione matematica (solitamente espressa come f(x)) può essere interpretata come una formula che ti permette di ricavare il valore di y in base a un dato valore di x. La funzione inversa di f(x) (che viene espressa come f-1(x)) è in pratica il procedimento opposto, grazie al quale si ottiene il valore di x una volta inserito quello di y. Trovare l’inverso di una funzione può sembrare un processo complicato, ma per le equazioni semplici basta la conoscenza delle operazioni algebriche di base. Continua a leggere per imparare a farlo.
Passaggi
-
1Scrivi la funzione sostituendo f(x) con y, se necessario. La formula dovrebbe presentarsi con la y, da sola, a un lato del segno di uguaglianza e i termini con x sull’altro lato. Se l’equazione è scritta con i termini di y e x (ad esempio 2 + y = 3x2), allora devi risolvere per y isolandola su un lato del segno “uguale”.
- Esempio: consideriamo la funzione f(x) = 5x - 2, che può essere scritta come y = 5x - 2 semplicemente sostituendo "f(x)" con y.
- Nota: f(x) è una notazione standard per indicare una funzione, ma se stai trattando più funzioni, ognuna di esse avrà una lettera diversa per renderne l’identificazione più semplice. Ad esempio, puoi scrivere g(x) e h(x) (che sono lettere altrettanto comuni per scrivere una funzione).
-
2Risolvi l’equazione per x. In altre parole svolgi le necessarie operazioni matematiche per isolare x su un lato del segno di uguaglianza. In questo passaggio i semplici principi algebrici ti saranno d’aiuto. Se x possiede un coefficiente numerico, dividi entrambi i lati dell’equazione per tale numero; se x viene sommato a un valore, sottrai quest’ultimo in entrambi i lati dell’equazione e così via.
- Ricorda di eseguire le operazioni su entrambi i termini presenti ai lati del segno di uguale.
- Esempio: consideriamo sempre l’equazione precedente e sommiamo in entrambi i lati il valore di 2. Questo ci porta a trascrivere la formula come: y + 2 = 5x. Ora dovremmo dividere entrambi i termini per 5 e otterremo: (y + 2)/5 = x. Infine, per rendere più semplice la lettura, portiamo la "x" sul lato sinistro dell’equazione e riscriviamo quest’ultima come: x = (y + 2)/5.
-
3Sostituisci le variabili. Cambia x con y e viceversa. L’equazione risultante è l’inversa di quella originale. In altre parole se inserisci il valore di x nell’equazione iniziale e ottieni una determinata soluzione, quando inserisci tale dato nell’equazione inversa (sempre per x) troverai di nuovo il valore di partenza!
- Esempio: dopo avere sostituito x e y otteniamo: y = (x + 2)/5.
-
4Sostituisci y con "f-1(x)". Le funzioni inverse sono espresse solitamente con la notazione f-1(x) = (termini in x) . Nota che, in questo caso, l’esponente -1 non significa che devi eseguire un'operazione di potenza sulla funzione. Si tratta solo di una scrittura convenzionale per indicare la funzione inversa dell’originale.
- Poiché elevare x alla -1 ti conduce a una soluzione frazionale (1/x) allora potresti pensare che f-1(x) sia un modo di scrivere "1/f(x)" che significa appunto inverso di f(x).
-
5Controlla il tuo lavoro. Prova a sostituire l’incognita x con una costante nella funzione originale. Se hai svolto i passaggi in maniera corretta, dovresti essere in grado di inserire il risultato nella funzione inversa e ritrovare la costante di partenza.
- Esempio: assegniamo a x il valore 4 all’interno dell’equazione di partenza. Questo ti porta a: f(x) = 5(4) - 2, quindi f(x) = 18.
- Ora sostituiamo x della funzione inversa con il risultato appena trovato, 18. Quindi avremo che y = (18 + 2)/5, semplificando: y = 20/5 = 4. 4 è il valore originale che abbiamo assegnato a x, quindi la nostra funzione inversa è corretta.
Pubblicità
Consigli
- Puoi liberamente passare da una notazione f(x) = y a una f^(-1)(x) = y senza problemi, quando stai eseguendo delle operazioni algebriche sulle tue funzioni. Tuttavia, può creare della confusione mantenere la funzione originale e la funzione inversa nella forma diretta; è meglio usare la notazione f(x) o f^(-1)(x), se non stai usando una delle due funzioni, che aiuta a distinguerle meglio.
- Nota che l'inverso di una funzione è, di solito, ma non sempre, anch’essa una funzione.
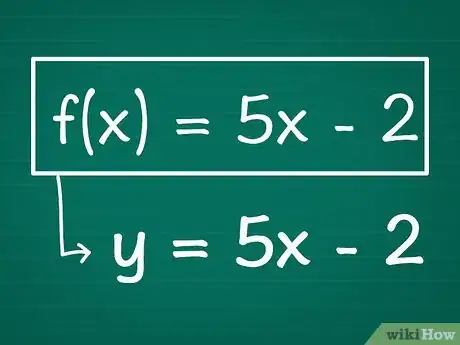
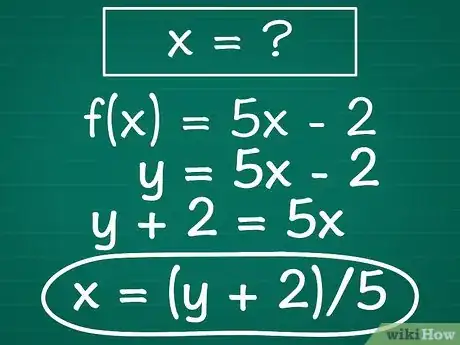
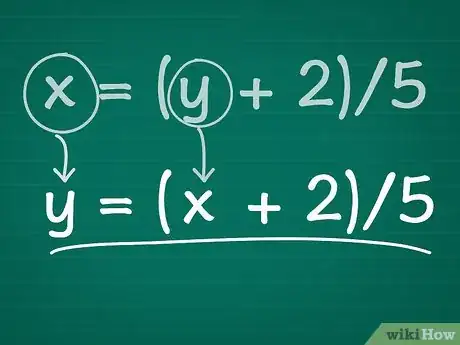
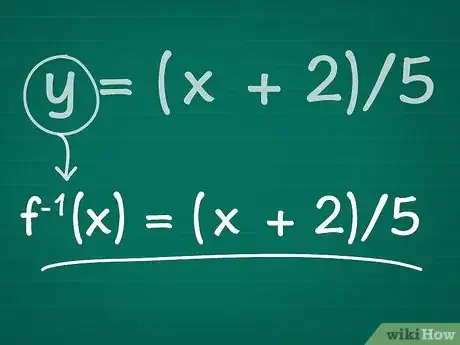
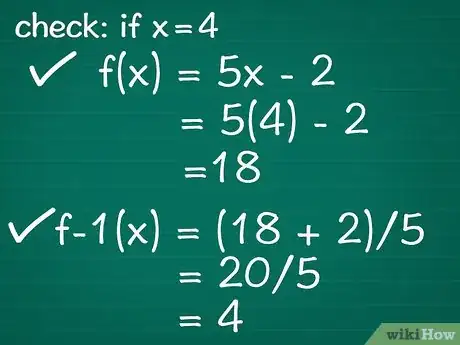




-to-Grams-(g)-Step-12-Version-4.webp)