Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 32 063 volte
Un’espressione algebrica è una formula matematica che contiene numeri e/o variabili. Anche se non può essere risolta dato che non contiene il segno “uguale” (=), può essere semplificata. Tuttavia, è possibile risolvere le equazioni algebriche, che contengono espressioni algebriche separate dal segno “uguale”. Se vuoi sapere come padroneggiare questo concetto matematico, continua a leggere.
Passaggi
Conoscere le Basi
-
1Cerca di capire la differenza tra espressione algebrica ed equazione algebrica. Un’espressione algebrica è una formula matematica che contiene numeri e/o variabili. Non contiene un segno di uguaglianza e non può essere risolta. Un’equazione algebrica invece può essere risolta e contiene una serie di espressioni algebriche separate da un segno di uguale. Ecco alcuni esempi:
- Espressione algebrica: 4x + 2
- Equazione algebrica: 4x + 2 = 100
-
2Comprendi come combinare i termini simili. Combinare i termini simili significa semplicemente sommare (o sottrarre) i termini di uguale grado. Questo significa che tutti gli elementi x2 possono essere combinati con altri elementi x2, che tutti i termini x3 possono essere combinati con altri termini x3 e che anche tutte le costanti, numeri che non sono legati ad alcuna variabile, come 8 o 5, possono essere sommati o combinati. Ecco alcuni esempi:
- 3x2 + 5 + 4x3 - x2 + 2x3 + 9 =
- 3x2 - x2 + 4x3 + 2x3 + 5 + 9 =
- 2x2 + 6x3 + 14
-
3Capisci come fattorizzare un numero. Se stai lavorando su un’equazione algebrica, cioè hai un’espressione per ciascun lato del segno di uguaglianza, allora puoi semplificarla usando un termine comune. Osserva i coefficienti di tutti i termini (i numeri che precedono le variabili, o costanti) e controlla se c’è un numero che puoi “eliminare” dividendo ogni termine per quel numero. Se lo puoi fare, puoi anche semplificare l’equazione e iniziare a risolverla. Ecco come:
- 3x + 15 = 9x + 30
- Ogni coefficiente è divisibile per 3. Ti basta “eliminare” il fattore 3 dividendo ogni termine per 3 e avrai semplificato l’equazione.
- 3x/3 + 15/3 = 9x/3 + 30/3
- x + 5 = 3x + 10
- 3x + 15 = 9x + 30
-
4Comprendi l’ordine in cui svolgere le operazioni. L’ordine delle operazioni, conosciuto anche con l’acronimo PEMDAS, spiega la sequenza in cui devono essere svolte le operazioni matematiche. L’ordine è: Parentesi, Esponenti, Moltiplicazione, Divisione, Addizione e Sottrazione. Ecco un esempio di come funziona:
- (3 + 5)2 x 10 + 4
- Prima viene P e quindi l’operazione tra parentesi:
- = (8)2 x 10 + 4
- Poi c’è E e quindi gli esponenti:
- = 64 x 10 + 4
- Poi si passa alla moltiplicazione:
- = 640 + 4
- E per ultima l’addizione:
- = 644
-
5Impara a isolare le variabili. Se stai risolvendo un’equazione algebrica, allora il tuo obiettivo è avere la variabile, di solito indicata con la lettera x, da un lato dell’equazione, e tutte le costanti dall’altro. Puoi isolare la variabile attraverso divisioni, moltiplicazioni, addizioni, sottrazioni, trovando la radice quadrata o tramite altre operazioni. Una volta isolata la x puoi risolvere l’equazione. Ecco come:
- 5x + 15 = 65
- 5x/5 + 15/5 = 65/5
- x + 3 = 13
- x = 10
Pubblicità
Risolvere un’Equazione Algebrica
-
1Risolvi una semplice equazione algebrica lineare. Un’equazione algebrica lineare contiene solo costanti e variabili di primo grado (niente esponenti o elementi strani). Per risolverla si usano semplicemente moltiplicazioni, divisioni, addizioni e sottrazioni per isolare e trovare la x. Ecco come si procede:
- 4x + 16 = 25 -3x
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16
- 7x = 9
- 7x/7 = 9/7
- x = 9/7
-
2Risolvi un’equazione algebrica con esponenti. Se l’equazione ha degli esponenti, allora tutto quello che devi fare è trovare un modo per isolare l’esponente da una parte dell’equazione e poi risolverla “rimuovendo” l’esponente stesso. Come? Trovando la radice sia dell’esponente sia della costante dall’altra parte dell’equazione. Ecco come fare:
- 2x2 + 12 = 44
- Per prima cosa, sottrai 12 da entrambi i lati:
- 2x2 + 12 -12 = 44 -12
- 2x2 = 32
- Poi, dividi per 2 da entrambi i lati:
- 2x2/2 = 32/2
- x2 = 16
- Risolvi estraendo la radice quadrata da entrambe le parti in modo da trasformare la x2 in x:
- √x2 = √16
- Scrivi entrambi i risultati: x = 4, -4
- 2x2 + 12 = 44
-
3Risolvi un’espressione algebrica contenente frazioni. Se vuoi risolvere un’equazione algebrica di questo tipo devi fare una moltiplicazione incrociata delle frazioni, combinare i termini simili e poi isolare la variabile. Ecco come fare:
- (x + 3)/6 = 2/3
- Per prima cosa, fai una moltiplicazione incrociata per eliminare la frazione. Devi moltiplicare il numeratore di una per il denominatore dell’altra:
- (x + 3) x 3 = 2 x 6
- 3x + 9 = 12
- Ora combina i termini simili. Combina le costanti, 9 e 12, sottraendo 9 da entrambi i lati:
- 3x + 9 - 9 = 12 - 9
- 3x = 3
- Isola la variabile, x, dividendo entrambi i lati per 3 e avrai il risultato:
- 3x/3 = 3/3
- x = 3
- (x + 3)/6 = 2/3
-
4Risolvi un’espressione algebrica con le radici. Se stai lavorando a un’equazione di questo tipo tutto ciò che devi fare è trovare un modo per elevare al quadrato entrambi i lati in modo da eliminare le radici e trovare la variabile. Ecco come fare:
- √(2x+9) – 5 = 0
- Per prima cosa, sposta tutto ciò che non è sotto radice dall’altro lato dell’equazione:
- √(2x+9) = 5
- Poi eleva al quadrato entrambe le parti in modo da rimuovere la radice:
- (√(2x+9))2 = 52
- 2x + 9 = 25
- A questo punto risolvi l’equazione come faresti normalmente, combinando le costanti e isolando la variabile:
- 2x = 25 – 9
- 2x = 16
- x = 8
- √(2x+9) – 5 = 0
-
5Risolvi un’espressione algebrica che contiene valori assoluti. Il valore assoluto di un numero rappresenta il suo valore indipendentemente dal segno “+” o “–” che lo precede; il valore assoluto è sempre positivo. Quindi, per esempio, il valore assoluto di -3 (scritto anche |3|) è semplicemente 3. Per trovare il valore assoluto, devi isolare il valore assoluto e poi risolvere due volte secondo x. La prima, semplicemente rimuovendo il valore assoluto e la seconda con i termini dall’altra parte dell’uguale cambiati di segno. Ecco come fare:
- Risolvi isolando il valore assoluto e poi rimuovilo:
- |4x +2| - 6 = 8
- |4x +2| = 8 + 6
- |4x +2| = 14
- 4x + 2 = 14
- 4x = 12
- x = 3
- Ora risolvi ancora cambiando il segno dei termini dall’altra parte dell’equazione dopo aver isolato il valore assoluto:
- |4x +2| = 14
- 4x + 2 = -14
- 4x = -14 -2
- 4x = -16
- 4x/4 = -16/4
- x = -4
- Scrivi entrambi i risultati: x = -4, 3
Pubblicità
Consigli
- Per fare un controllo incrociato dei risultati, visita wolfram-alpha.com. Fornisce il risultato e spesso anche i due passaggi.
- Una volta che avrai finito, sostituisci la variabile con il risultato ottenuto e risolvi la somma per vedere se quello che hai fatto ha senso. Se è così, congratulazioni! Hai appena risolto un’equazione algebrica!
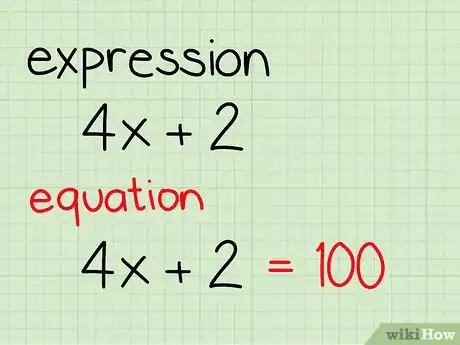
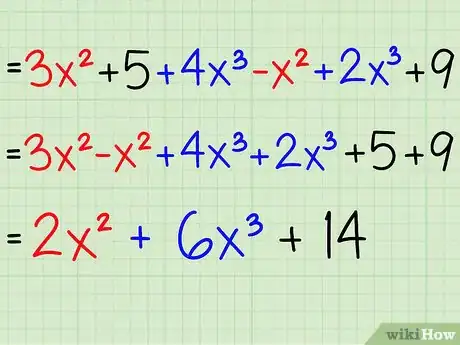
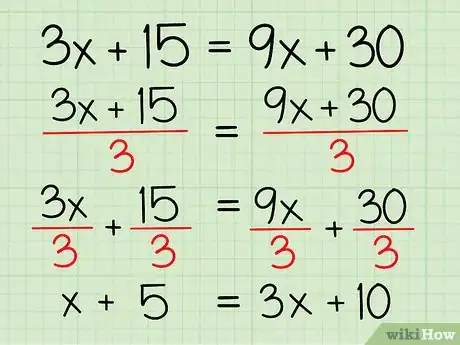
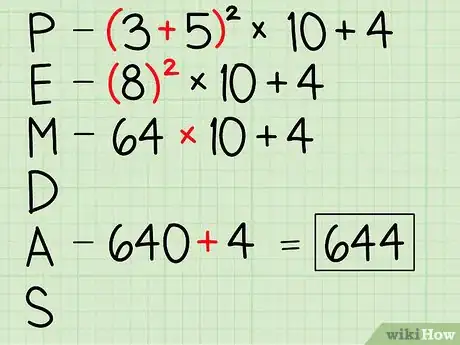

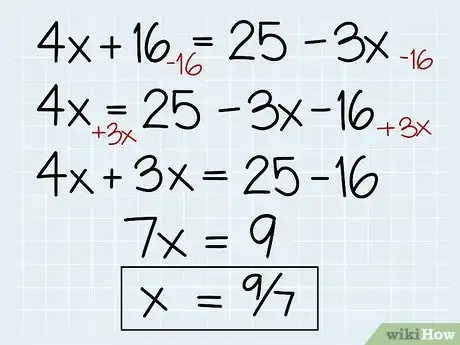
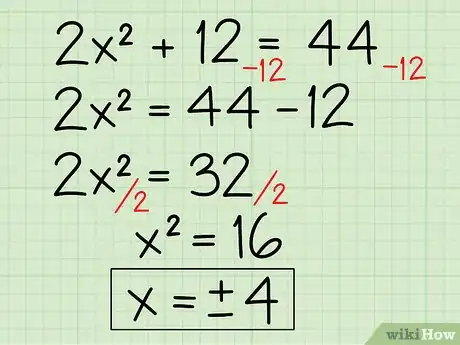
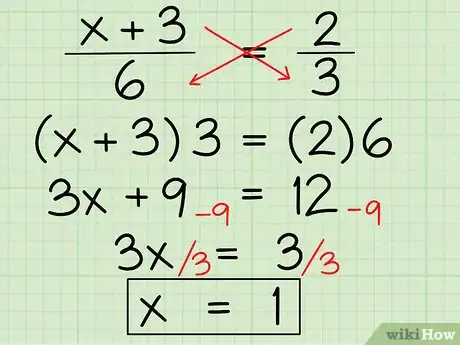
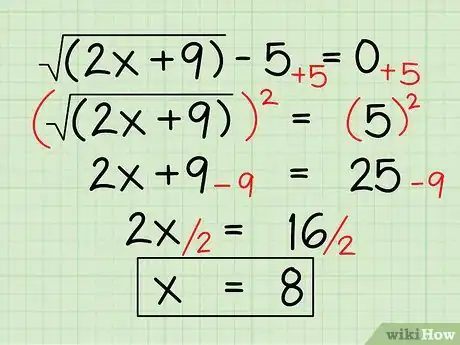
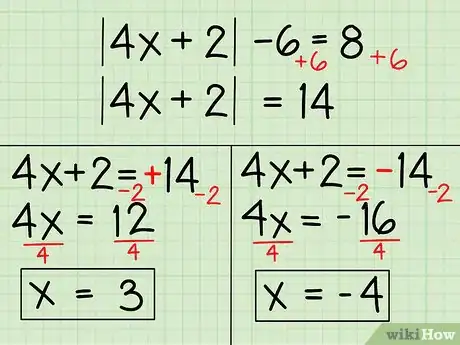



-to-Grams-(g)-Step-12-Version-4.webp)














-to-Grams-(g)-Step-12-Version-4.webp)
