wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 72 386 volte
Pi greco (π) è uno dei numeri più importanti e affascinanti per chi è appassionato di matematica. Arrotondata a 3,14, è una costante utilizzata per calcolare la lunghezza della circonferenza di un cerchio conoscendo la misura del raggio. È anche un numero irrazionale, vale a dire un numero del quale possono essere calcolate un numero infinito di cifre decimali senza ripetizioni. Questo rende difficile, ma non impossibile, un calcolo preciso.
Passaggi
Calcolare il Valore di Pi Greco Usando le Misurazioni di una Circonferenza
-
1Accertati di usare una circonferenza perfetta. Questo metodo non funziona con ellissi, ovali o qualsiasi cosa che non sia un cerchio. Un cerchio è definito come l'insieme dei punti di un piano che sono equidistanti da un singolo punto centrale. I coperchi dei barattoli sono degli oggetti che trovi in casa, e che si prestano bene per l'esperimento che stai per fare.
-
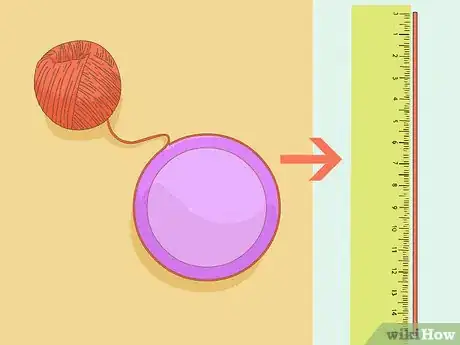
2Misura la circonferenza il più accuratamente possibile. La circonferenza è la misura della linea curva che delimita il cerchio. Dal momento che la circonferenza è rotonda, può essere difficile misurarla (ecco perché pi greco è così importante).
- Avvolgi una cordicella attorno al cerchio, più stretta possibile. Segna sulla cordicella i punti in cui le due estremità si incontrano, e misura la lunghezza della cordicella con un righello.
-
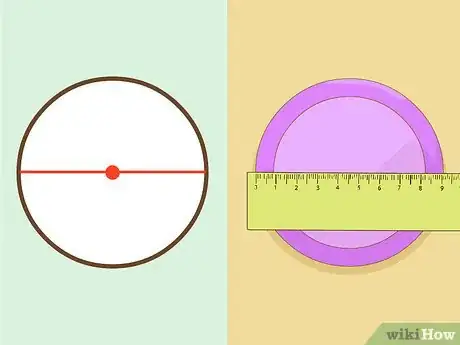
3Misura il diametro del cerchio. Il diametro è il segmento che unisce le due estremità del cerchio, passando per il centro.
-
4Usa la formula corretta. La misura della circonferenza di un cerchio si trova con la formula C= π*d = 2*π*r. Quindi pi greco è uguale al rapporto fra la misura della circonferenza e il diametro. Calcola questo rapporto con una calcolatrice: il risultato dovrebbe essere approssimativamente 3,14.
-
5Per avere un risultato più accurato, ripeti il procedimento con cerchi di dimensioni differenti, e fai la media dei risultati. Le misurazioni potrebbero non essere precise in alcuni casi, ripetendo il procedimento per un numero significativo di volte, si dovrebbe approssimare pi greco ad un valore sufficientemente accurato.Pubblicità
Calcolare il Pi Greco Usando una Serie Infinita
-
1Usa la serie di Gregory-Leibniz. I matematici hanno trovato differenti serie matematiche che, se calcolate sommando un numero infinito di termini, generano un'approssimazione sufficientemente accurata di pi greco per un numero abbastanza grande di decimali. Alcune di esse sono talmente complesse da richiedere dei supercomputer per calcolarle. Una delle più semplici, comunque, è la serie di Gregory-Leibniz. Anche se non è molto efficiente, genera un numero sempre più vicino a pi greco ad ogni iterazione, arrivando ad una approssimazione sufficientemente accurata con 10 cifre decimali con 500.000 iterazioni. Ecco la formula da utilizzare.
- π = (4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Parti da 4, e sottrai 4 diviso 3. Poi somma 4 diviso 5. Quindi sottrai 4 diviso 7. Continua sommando e sottraendo alternativamente frazioni in cui il numeratore è 4 e il denominatore è il numero dispari successivo rispetto al precedente. Più volte lo fai, più ti avvicini al valore di pi greco.
-
2Prova la serie di Nilakantha. È un'altra serie infinita per calcolare pi greco, facilmente comprensibile. Anche se più complessa, converge a pi greco molto più velocemente della formula di Leibniz.
- π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - (4/(12*13*14) ...
- Per calcolare questa formula, parti da tre e inizia ad alternare somme e sottrazioni di frazioni in cui il numeratore è 4 e il denominatore è il prodotto di tre numeri interi consecutivi che vengono incrementati ad ogni nuova iterazione. Il denominatore di ogni frazione successiva è il prodotto di tre numeri, il primo dei quali è il più alto della frazione precedente. Ripeti il procedimento anche solo per poche volte e otterrai un risultato abbastanza vicino a pi greco.
Pubblicità
Calcolare il Pi Usando un Limit
-
1Per prima cosa, scegli in numero grande. Più grande è il numero, più accurati risulteranno i tuoi calcoli.
-
2Quindi inserisci il numero al posto della "x" in questa formula per calcolare il pi greco: x * sin(180 / x). Perché funzioni, assicurati che la calcolatrice sia settata su Gradi. La ragione per cui è chiamato "limite" è che il risultato è "limitato" al pi greco: all'aumentare del numero x, aumenta l'approssimazione al valore di pi.Pubblicità
Funzione Arcoseno / Seno Inverso
-
1Scegli un numero qualunque tra -1 e 1. Fai così perché la funzione arcoseno non è definita per argomenti maggiori di 1 o inferiori a -1.
-
2Inserisci il numero nella formula seguente. Il risultato sarà molto vicino a pi.
- pi = 2 * (Arcsin(rad(1 - x^2)) + ass(Arcsin(x))).
- Arcsin indica l'inverso del seno in radianti.
- Rad è l'abbreviazione di radice quadrata.
- Ass è l'abbreviazione di valore assoluto.
- x^2 indica un esponente, in questo caso x al quadrato.
Pubblicità - pi = 2 * (Arcsin(rad(1 - x^2)) + ass(Arcsin(x))).
Consigli
- Calcolare il pi greco può essere una sfida divertente, ma un così grande sforzo non produce risultati significativi. Gli astrofisici utilizzano il pi greco approssimato a 39 cifre decimali in calcoli tanto precisi dal richiedere un'accuratezza paragonabile alla dimensione di un atomo.






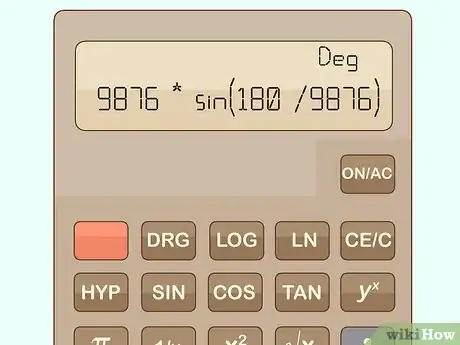




-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
