wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 37 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 26 236 volte
Il Coefficiente di Correlazione per Ranghi di Spearman consente di identificare il grado di correlazione tra due variabili in una funzione monotona (ad esempio, nel caso di un aumento proporzionale o proporzionalmente inverso tra due numeri). Segui questa semplice guida per calcolare manualmente, o sapere come calcolare, il coefficiente di correlazione in Excel o nel programma R.
Passaggi
Calcolo Manuale
-
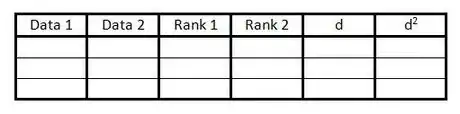
1Crea una tabella con i tuoi dati. Questa tabella organizzerà le informazioni necessarie per calcolare il Coefficiente di Correlazione per Ranghi di Spearman. Avrai bisogno di:
- 6 colonne, con le intestazioni come illustrate di seguito.
- Tante righe quante sono le coppie di dati a disposizione.
-
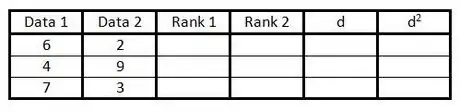
2Compila le prime due colonne con le tue coppie di dati.
-
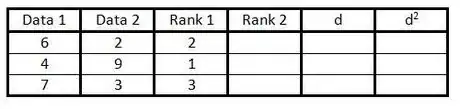
3Nella terza colonna classifica i dati della prima colonna da 1 a n (il numero dei dati a disposizione). Classifica il numero più basso con rango 1, il successivo numero più basso con rango 2, e così via.
-
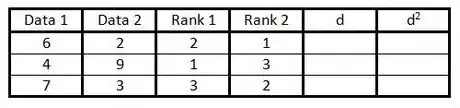
4Opera sulla quarta colonna come nel passaggio 3, ma classifica la seconda colonna invece della prima.
-
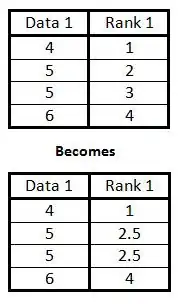
Se due (o più) dati in una colonna sono identici, trova la media dei ranghi, come se i dati fossero stati classificati normalmente, poi classifica i dati usando questa media.
Nell'esempio riportato a destra, ci sono due 5 che avrebbero teoricamente un rango di 2 e 3. Poiché ci sono due 5, usa la media del loro ranghi. La media di 2 e 3 è 2,5, quindi assegna il rango 2,5 a entrambi i numeri 5.
-
Se due (o più) dati in una colonna sono identici, trova la media dei ranghi, come se i dati fossero stati classificati normalmente, poi classifica i dati usando questa media.
-
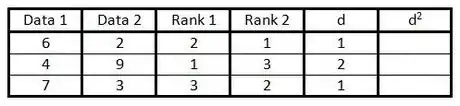
5Nella colonna "d" calcola la differenza tra i due numeri in ciascuna coppia di ranghi. Ovvero, se uno dei numeri è classificato nel rango 1 e l'altro nel rango 3, la differenza tra i due darebbe come risultato 2. (Il segno del numero non ha importanza, dato che nel passaggio successivo questo valore sarà elevato al quadrato).
-
6
-
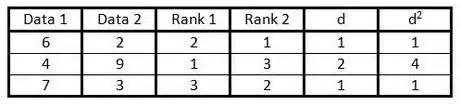
7Eleva al quadrato ciascuno dei numeri nella colonna "d" e scrivi questi valori nella colonna "d2".
-
8
-
9
-
10
-
11Interpreta il risultato. Può variare tra -1 e 1.
- Vicino a -1 - Correlazione negativa.
- Vicino a 0 - Nessuna correlazione lineare.
- Vicino a 1 - Correlazione positiva.
Pubblicità
In Excel
-
1Crea nuove colonne con i ranghi delle colonne esistenti. Ad esempio, se i dati sono nella colonna A2:A11, userai la formula "=RANGO(A2,A$2:A$11)", copiandola in tutte le righe e le colonne.
-
2In una nuova cella, crea una correlazione tra le due colonne del rango con una funzione simile a "=CORRELAZIONE(C2:C11,D2:D11)". In questo caso, C e D corrisponderebbero alle colonne dei ranghi. La cella della correlazione fornirà la correlazione dei ranghi di Spearman.Pubblicità
Usando il Programma R
-
1Se non l'avessi già, scarica il programma R. (Vedi http://www.r-project.org).
-
2Salva i contenuti in un file CSV con i dati che desideri correlare nelle prime due colonne. Clicca sul menu e scegli "Salva con nome".
-
3Apri il programma R. Se sei sul terminale, sarà sufficiente eseguire R. Sul desktop, clicca sul logo del programma R.
-
4Digita i comandi:
- d <- read.csv ("NOME_DEL_TUO_CSV.csv") e premi invio
- correlazione(rango(d[,1]),rango(d[,2]))
Pubblicità
Consigli
- La maggior parte dei dati dovrebbero contenere almeno 5 coppie di dati per identificare una tendenza (nell'esempio sono state utilizzate 3 coppie di dati per rendere più facile la dimostrazione).
Avvertenze
- Il Coefficiente di Correlazione di Spearman identificherà solamente il grado di correlazione li dove sussiste un aumento o una diminuzione costante dei dati. Se si utilizza un diagramma a dispersione dei dati, il coefficiente di Spearman non fornirà una rappresentazione accurata di questa correlazione.
- Questa formula si basa sul presupposto che non esistono correlazioni tra le variabili. Quando esistono delle correlazioni come quella illustrata nell'esempio, è necessario utilizzare l'indice di correlazione di Pearson basato sui ranghi.
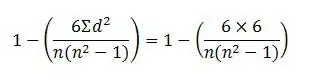
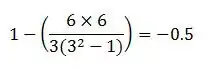



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
