Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 4 439 volte
Calcolare il numero di termini di una progressione aritmetica potrebbe sembrare un'operazione complessa, ma in realtà è un procedimento semplice e lineare. Tutto quello che occorre fare è inserire i valori noti della progressione nella formula tn = a + (n - 1) d, e risolvere l'equazione in base a n, che rappresenta il numero dei termini della sequenza. Nota che la variabile tn della formula rappresenta l'ultimo numero della sequenza, il parametro a è il primo termine della progressione e il parametro d rappresenta la ragione, cioè la differenza costante esistente fra ciascun termine della sequenza numerica e quello precedente.
Passaggi
-
1Identifica il primo, il secondo e l'ultimo numero della progressione aritmetica in esame. Normalmente, nel caso di problemi matematici come quello in oggetto, i primi tre (o più) termini della sequenza e l'ultimo sono sempre noti.[1]
- Per esempio, ipotizza di dover esaminare la seguente progressione: 107, 101, 95…-61. In questo caso il primo numero della sequenza è 107, il secondo è 101 e l'ultimo è -61. Per risolvere il problema hai la necessità di usare tutte queste informazioni.
-
2Sottrai il primo termine della sequenza dal secondo per calcolare la ragione della progressione. Nell'esempio proposto il primo numero è 107, mentre il secondo è 101, quindi eseguendo i calcoli otterrai 107 – 101 = -6. A questo punto sai che la ragione della progressione aritmetica in esame è pari a -6.[2]
-
3Usa la formula tn = a + (n - 1) d e risolvi i calcoli in base a n. Sostituisci i parametri dell'equazione con i valori noti: tn con l'ultimo numero della sequenza, a con il primo termine della progressione e d con la ragione. Esegui i calcoli per risolvere l'equazione in base a n.[3]
- Proseguendo con l'esempio precedente otterrai -61 = 107 + (n - 1) -6. Inizia sottraendo il valore 107 da entrambi i membri dell'equazione ottenendo -168 = (n - 1) -6. A questo punto dividi entrambi i membri per il valore -6 ottenendo 28 = n - 1. Infine somma il valore 1 a entrambi i membri ottenendo n = 29.
Pubblicità
Consigli
- La differenza fra il primo numero della sequenza e l'ultimo è sempre divisibile per la ragione della progressione aritmetica.
Avvertenze
- Non confondere la differenza esistente fra il primo numero della progressione aritmetica e l'ultimo con la ragione della progressione stessa.
Riferimenti
- ↑ www.youtu.be/hGiuMNIR7Gk?t=13
- ↑ https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/finding-the-number-of-terms-in-a-finite-arithmetic-sequence/
- ↑ www.youtu.be/hGiuMNIR7Gk?t=59
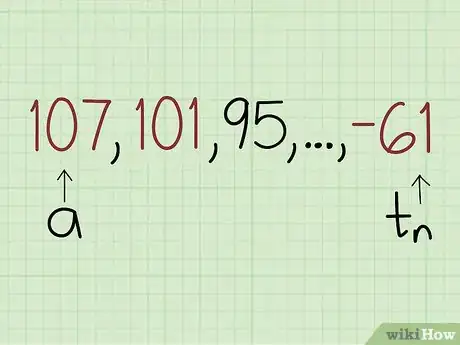
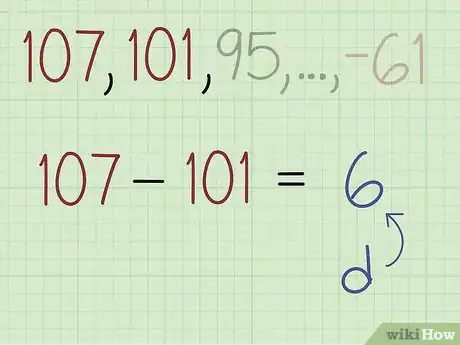
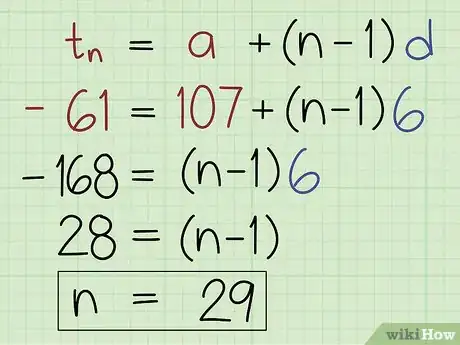



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 4 439 volte