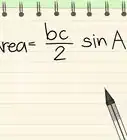Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 88 078 volte
Il perimetro di un quadrato, così come quello di una qualsiasi forma geometrica, è la misura della lunghezza del contorno. Il quadrato è un quadrilatero regolare, il che significa che ha quattro lati uguali e quattro angoli retti. Poiché tutti i lati sono uguali, non è difficile calcolare il perimetro! Questo tutorial ti mostrerà per prima cosa come calcolare il perimetro di un quadrato di cui conosci la misura del lato e poi quello di un quadrato di cui conosci l’area. Infine tratterà un quadrato inscritto in una circonferenza di raggio noto.
Passaggi
Calcolare il Perimetro di un Quadrato con un Lato Noto
-
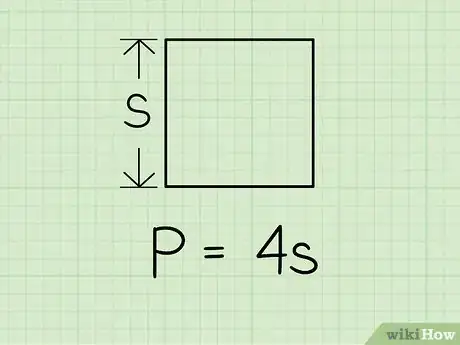
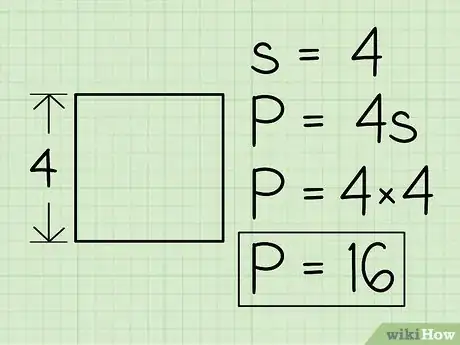
1Riporta alla memoria la formula per calcolare il perimetro di un quadrato. Per un quadrato di lato s, il perimetro è semplicemente: P=4s.
-
2Determina la lunghezza di un lato e moltiplicala per quattro. In base al compito che ti viene assegnato, dovrai rilevare il valore del lato con un righello oppure dedurlo da altre informazioni. Ecco alcuni esempi:
- Se il lato del quadrato misura 4, allora: P = 4 * 4 = 16.
- Se il lato del quadrato misura 6, allora: P = 6 * 6 = 64.
Pubblicità
Calcolare il Perimetro di un Quadrato di Area Nota
-
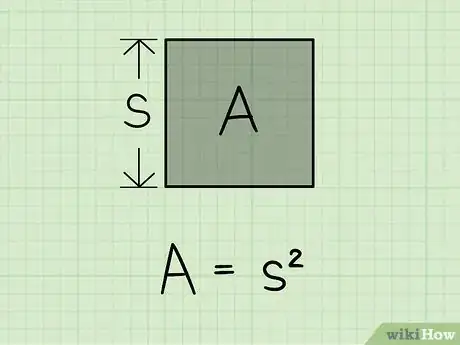
1Ripassa la formula dell’area del quadrato. L’area di ogni rettangolo (ricorda che il quadrato è un rettangolo speciale) viene definita come il prodotto della base per l’altezza. Poiché sia la base che l’altezza di un quadrato hanno lo stesso valore, un quadrato di lato s possiede l’area pari a s*s cioè: A = s2.
-
2Calcola la radice quadrata dell’area. Questa operazione ti fornisce il valore del lato. Nella maggior parte dei casi dovrai usare una calcolatrice per estrarre la radice: digita il valore dell’area e poi premi il tasto di radice quadrata (√). Puoi anche imparare a calcolare la radice quadrata a mano!
- Se l’area è pari a 20, allora il lato è pari a s =√20 cioè 4,472.
- Se l’area è pari a 25, allora il lato è pari a s =√25 cioè 5.
-
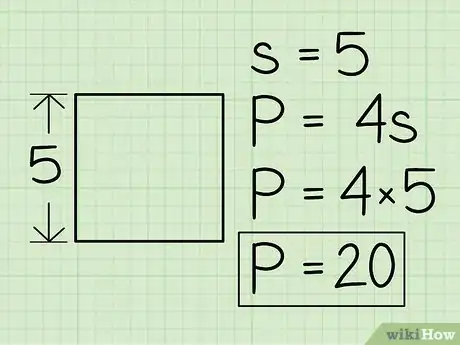
3Moltiplica il valore del lato per 4 e otterrai il perimetro. Prendi la lunghezza s che hai appena ricavato e inseriscila nella formula del perimetro: P = 4s!
- Per il quadrato di area pari a 20 e lato 4,472, il perimetro è P = 4 * 4,472 cioè 17,888.
- Per il quadrato di area pari a 25 e lato 5, il perimetro è P = 4 * 5 cioè 20.
Pubblicità
Calcolare il Perimetro di un Quadrato Inscritto in un Cerchio di Raggio Noto
-
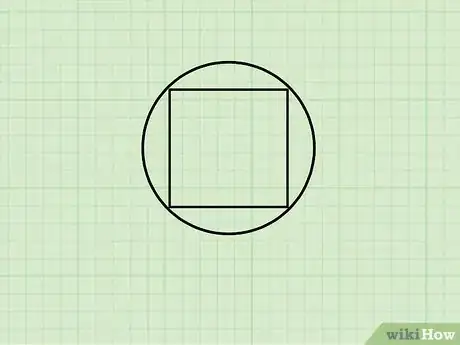
1Comprendi cos’è un quadrato inscritto. Le forme geometriche inscritte in altre sono presenti molto spesso nei test e nei compiti in classe, quindi è importante conoscerle e saperne calcolare i vari elementi. Un quadrato inscritto in un cerchio viene disegnato all’interno della circonferenza in modo che i 4 vertici giacciano sulla circonferenza stessa.
-
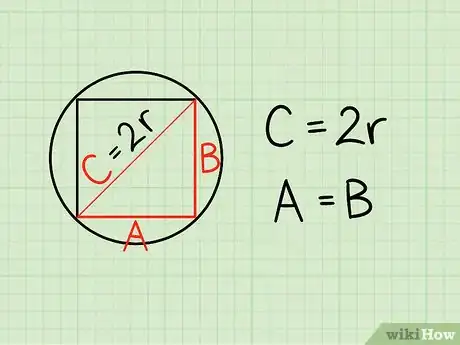
2Ripassa la relazione che intercorre fra il raggio della circonferenza e la lunghezza del lato del quadrato. La distanza dal centro del quadrato a uno dei suoi angoli è pari al valore del raggio della circonferenza. Per calcolare la lunghezza s del lato, devi prima immaginare di tagliare il quadrato in diagonale e formare due triangoli retti. Ciascuno di questi triangoli ha i cateti a e b uguali fra loro e un' ipotenusa c che conosci perché è pari al diametro della circonferenza (due volte il raggio o 2r).
-
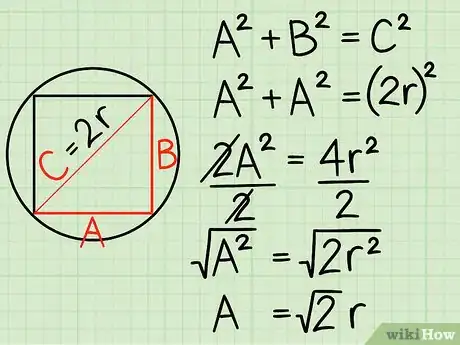
3Usa il Teorema di Pitagora per trovare la lunghezza del lato. Questo teorema afferma che per ogni triangolo rettangolo con cateti a e b e l’ipotenusa c, a2 + b2 = c2. Poiché a e b sono fra loro uguali (ricorda che sono anche i lati di un quadrato!) allora puoi affermare che c = 2r e riscrivere l’equazione in forma semplificata come segue:
- a2 + a2 = (2r)2"', ora semplifica l’equazione:
- 2a2 = 4(r)2, dividi entrambi i lati dell’uguaglianza per 2:
- (a2) = 2(r)2, ora estrai la radice quadrata da entrambi i valori:
- a = √(2r). La lunghezza s di un quadrato inscritto in un cerchio è pari a √(2r).
-
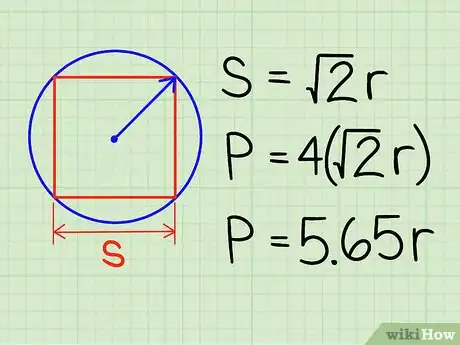
4Moltiplica il valore della lunghezza del lato per 4 e trova il perimetro. In questo caso l’equazione è P = 4√(2r). Per la proprietà distributiva degli esponenti puoi affermare che 4√(2r) è uguale a 4√2 * 4√r, quindi puoi semplificare ulteriormente l’equazione: il perimetro di ogni quadrato inscritto in un cerchio con raggio r è definito come P = 5,657r
-
5Risolvi l’equazione. Considera un quadrato inscritto in un cerchio di raggio 10. Questo significa che la diagonale è pari a 2*10 = 20. Usa il Teorema di Pitagora e saprai che: 2(a2) = 202, quindi 2a2 = 400. Ora dividi entrambi i lati a metà: a2 = 200. Estrai la radice e trovi che: a = 14,142. Moltiplica questo risultato per 4 e trovi il perimetro del quadrato: P = 56,57.
- Nota che avresti potuto ottenere lo stesso risultato semplicemente moltiplicando il raggio (10) per 5,657. Quindi: 10 * 5,567 = 56,57; tuttavia non è semplice ricordare questa costante durante un esame, è molto meglio imparare il procedimento qui spiegato.
Pubblicità
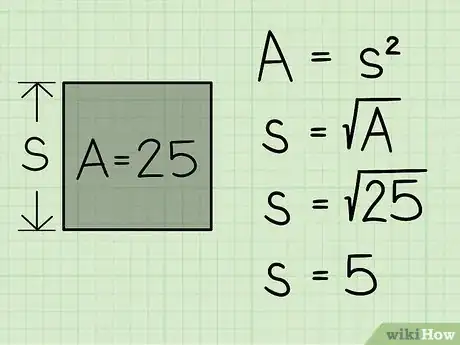
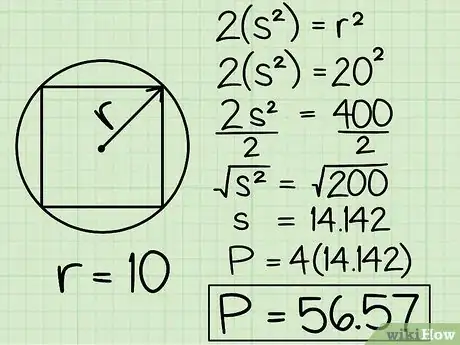





-to-Grams-(g)-Step-12-Version-4.webp)