Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 102 152 volte
Il rettangolo è un quadrilatero con i lati uguali a coppie e con quattro angoli retti. Per trovare l'area di un rettangolo, tutto ciò che devi fare è moltiplicare la base per l'altezza. Per capire come calcolare l'area di un rettangolo, segui questi semplici passaggi.
Passaggi
Capire le Caratteristiche Base del Rettangolo
-
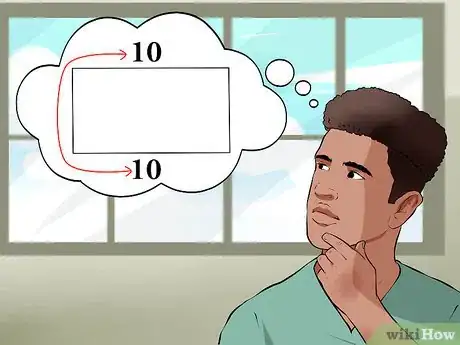
1Capisci cos'è un rettangolo. Il rettangolo è un quadrilatero, ovvero un poligono formato da quattro lati. I lati opposti sono uguali, quindi le due basi e le due altezze sono uguali. Se il lato di un rettangolo per esempio misura 10, anche quello opposto ad esso misurerà 10.
- Inoltre, ogni quadrato è anche un rettangolo, ma non tutti i rettangoli sono anche quadrati. Puoi quindi calcolare l'area di un quadrato considerandolo un rettangolo.
-
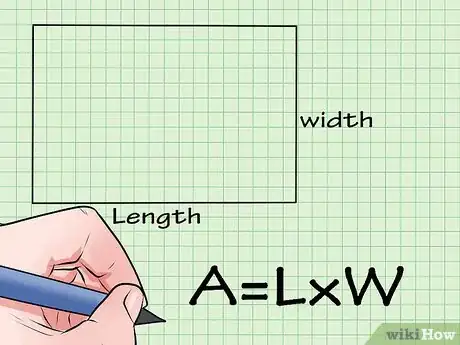
2Impara a memoria la formula per calcolare l'area di un rettangolo. La formula è semplice: A = b * h. Significa che l'area è uguale alla base moltiplicata per l'altezza.Pubblicità
Trovare l'Area di un Rettangolo
-
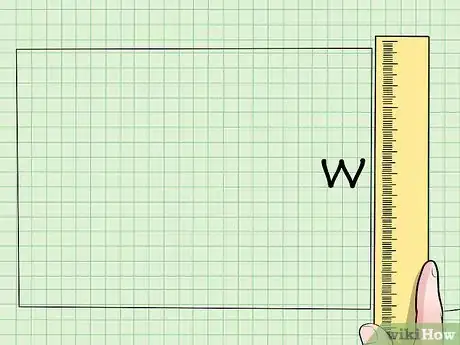
1Scopri la misura della base. Nella maggior parte dei problemi questa ti verrà data, altrimenti la puoi trovare con un righello.
- Nota che il segno doppio sulle basi del rettangolo in figura sta ad indicare che sono uguali tra loro.
-
2Trova l'altezza del rettangolo. Usa il metodo di prima.
- Nota che il segno sulle due altezze del rettangolo in figura sta ad indicare che sono uguali tra loro.
-
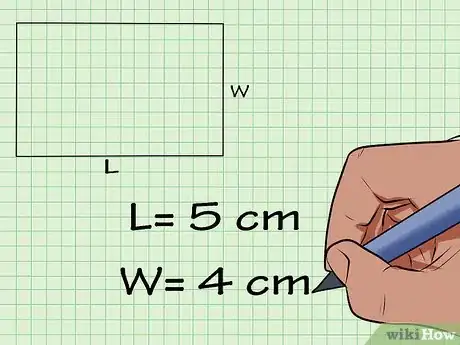
3Scrivi affiancate le misure di base e altezza. Nel nostro esempio, la base è 5 cm e l'altezza 4 cm.
-
4Moltiplica la base per l'altezza. La base è 5 cm e l'altezza è 4 cm, quindi per trovare l'area basterà sostituire questi valori nella formula A = b * h.
- A = 4 cm * 5 cm
- A = 20 cm^2
-
5Esprimi il risultato in centimetri quadrati. Il risultato finale è 20 cm^2, ovvero "venti centimetri quadrati".
- Puoi scrivere il risultato finale in due modi: o 20 cmq o 20 cm^2.
Pubblicità
Trovare l'Area Sapendo solo una delle due Dimensioni e la Diagonale
-
1Capisci il teorema di Pitagora. Il teorema di Pitagora è una formula per trovare il terzo lato di un triangolo rettangolo conoscendo la misura degli altri due. Puoi usarla per trovare l'ipotenusa di un triangolo, ovvero il lato più lungo, oppure uno dei due cateti, che sono i lati che formano l'angolo retto.
- Dato che il rettangolo è formato da quattro angoli retti, la diagonale che divide la figura a metà formerà due triangoli rettangoli, ai quali potrai applicare il teorema di Pitagora.
- Il teorema è: a^2 + b^2 = c^2, dove a e b sono i cateti e c è l'ipotenusa.
-
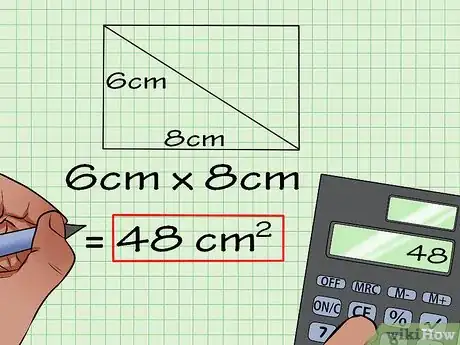
2Usa il teorema di Pitagora per trovare la dimensione mancante del triangolo. Mettiamo che tu abbia un rettangolo di base 6 cm e con una diagonale di 10 cm. Usa 6 cm come primo cateto, b per l'altro e 10 cm come ipotenusa. Insomma, basta sostituire nella formula del teorema di Pitagora le misure conosciute e risolvere. Ecco come:
- Es: 6^2 + b^2 = 10^2
- 36 + b^2 = 100
- b^2 = 100 - 36
- b^2 = 64
- Radice Quadrata (b) = radice quadrata (64)
- b = 8
- La misura dell'altro cateto del rettangolo, che corrisponde all'altra dimensione del rettangolo, è 8 cm.
-
3Moltiplica la base per l'altezza. Ora che hai sfruttato il teorema di Pitagora per trovare base e altezza del rettangolo, devi solo moltiplicarle tra loro.
- Es: 6 cm * 8 cm = 48 cm^2
-
4Esprimi il risultato in centimetri quadrati. Il risultato finale è 48 cm^2, o 48 cmq.Pubblicità
Consigli
- Tutti i quadrati sono rettangoli, ma non tutti i rettangoli sono quadrati.
- Quando devi calcolare l'area di un poligono, il risultato va sempre espresso al quadrato.
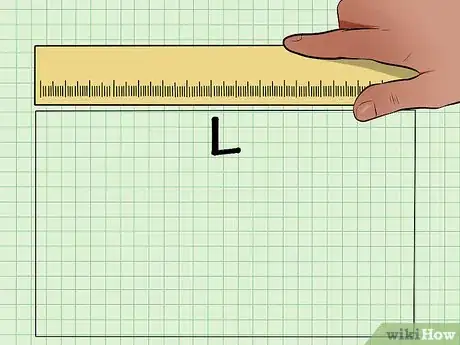










-to-Grams-(g)-Step-12-Version-4.webp)