Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 34 687 volte
Un'ellisse è una figura geometrica bidimensionale che assomiglia a un cerchio schiacciato a due estremità. L'equazione da utilizzare per calcolare l'area di un'ellisse è molto simile a quella usata per calcolare l'area di un cerchio. L'aspetto importante da ricordare è che l'ellisse è caratterizzata da due misure importanti: il raggio maggiore e il raggio minore.
Passaggi
Calcolare l'Area dell'Ellisse
-
1Individua il raggio maggiore dell'ellisse. Si tratta della distanza che separa il centro della figura dal punto più lontano della curva. Visualizzalo come il raggio relativo alla parte più "allungata" dell'ellisse. Procedi a misurare il raggio maggiore oppure individuane il valore all'interno del grafico o del testo del problema che ti è stato fornito. In questo esempio chiameremo questo valore a.
- Questo elemento dell'ellisse è conosciuto anche come "semiasse maggiore".[1]
-
2Individua il raggio minore. Si tratta della distanza che separa il centro dell'ellisse dal punto più vicino della curva. Questo valore lo chiameremo b.
- Il raggio maggiore e il raggio minore sono perpendicolari fra loro, quindi formano un angolo di 90°. Questo dato è solo informativo, dato che per calcolare l'area di un'ellisse non serve calcolare alcun angolo.
- Questo elemento dell'ellisse è conosciuto anche come "semiasse minore".
-
3Calcola l'area dell'ellisse. L'equazione per farlo è la seguente: a x b x π. Dato che stiamo moltiplicando fra loro due lunghezze, il risultato sarà espresso in unità di misura quadrate.
- Per esempio, ipotizziamo di calcolare l'area di un'ellisse avente il raggio maggiore pari a 5 unità e il raggio minore pari a 3 unità. L'area della figura sarà pari a 3 x 5 x π, cioè a circa 47 unità quadrate.
- Se non hai a disposizione una calcolatrice o se quella che hai non è dotata del tasto funzione per calcolare il π, puoi sostituire questa costante con il valore arrotondato di "3,14".
Pubblicità
Comprendere le Basi del Calcolo
-
1Analizza l'area di un cerchio. L'area di un cerchio è pari a πr2, che equivale a eseguire questo calcolo: π x r x r. Se trattiamo il nostro cerchio come un'ellisse, come dovremmo procedere per calcolarne l'area? Per prima cosa dobbiamo misurarne il raggio in una direzione qualunque ottenendo: r. A questo punto, passiamo a misurare il secondo raggio utilizzando un angolo di 90° rispetto al primo ottenendo sempre: r. Sostituendo i nostri valori all'interno dell'equazione per calcolare l'area di un'ellisse otterremo: π x r x r! Come abbiamo dimostrato, il cerchio non è altro che un caso speciale di ellisse.[2]
-
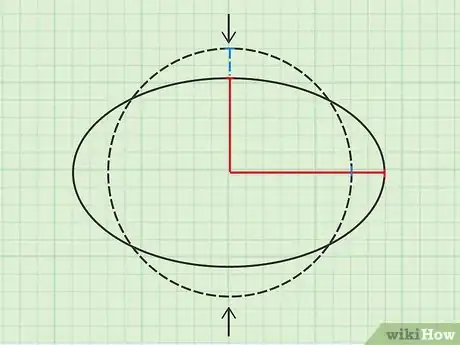
2Visualizza un cerchio schiacciato all'estremità superiore e inferiore. Immagina di disegnare un cerchio e di comprimerlo alle estremità per ottenere un'ellisse. In questo modo, un raggio tenderà ad accorciarsi, mentre il secondo tenderà ad allungarsi. L'area della figura rimarrà invariata dato che il cerchio non è stato ingrandito o rimpicciolito, ma solo deformato. Finché all'interno dell'equazione fornita si usano i raggi corretti dell'ellisse, quello maggiore andrà a compensare quello minore, dando sempre come risultato l'area totale della figura.Pubblicità
Consigli
- Se vuoi avere la dimostrazione matematica della correttezza dell'equazione per il calcolo dell'area di un'ellisse, devi imparare a utilizzare gli integrali.[3]


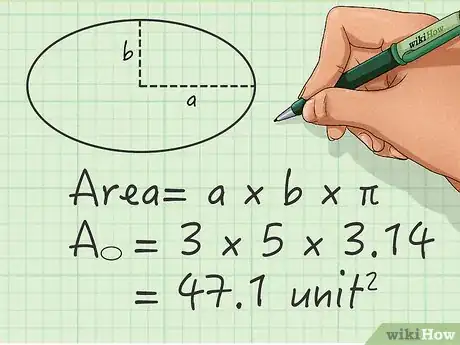
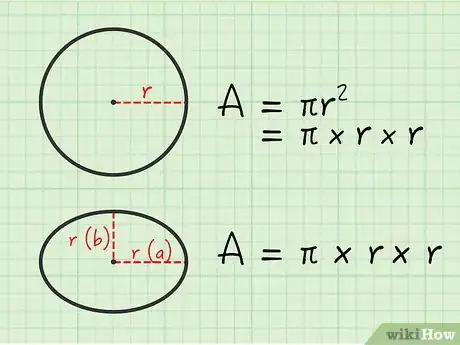



-to-Grams-(g)-Step-12-Version-4.webp)














-to-Grams-(g)-Step-12-Version-4.webp)
