Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 121 749 volte
Calcolare l'area di un quadrato è un'operazione molto semplice, a patto di conoscere alcune informazioni fondamentali, come la lunghezza di un lato, il perimetro o la lunghezza della diagonale. Prosegui nella lettura per scoprire come fare.
Passaggi
Usare la Lunghezza di un Lato
-
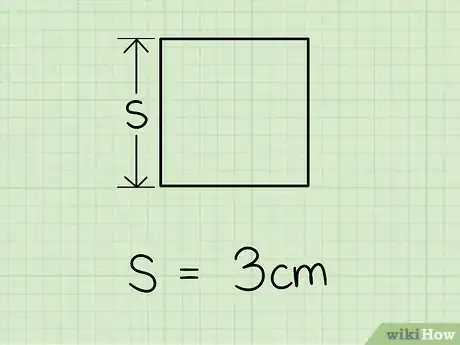
1Prendi nota della misura del lato. Ipotizza di dover lavorare su un quadrato che abbia un lato che misura 3 cm.
-
2Comprendi il principio che sta alla base della formula matematica per calcolare l'area di un quadrato (Area=Lato^2). Dato che tutti i lati di un quadrato sono uguali, per calcolarne l'area basta semplicemente moltiplicare la lunghezza per se stessa. Nell'esempio il lato del quadrato misura 3 cm, quindi dovrai elevare al quadrato tale valore per ottenere l'area della figura: 3 x 3 = 9 cm2.
-
3Non dimenticare di usare le unità di misura quadrate che in questo caso sono centimetri quadrati.
- Elevare al quadrato la lunghezza di un lato del quadrato corrisponde esattamente a moltiplicare la lunghezza della base della figura per l'altezza, l'equivalente della formula per calcolare l'area di qualsiasi parallelogramma rettangolo.
Pubblicità
Usare la Diagonale
-
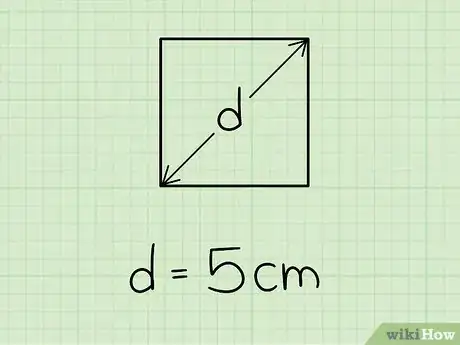
1Misura la lunghezza della diagonale del quadrato su cui stai lavorando.
-
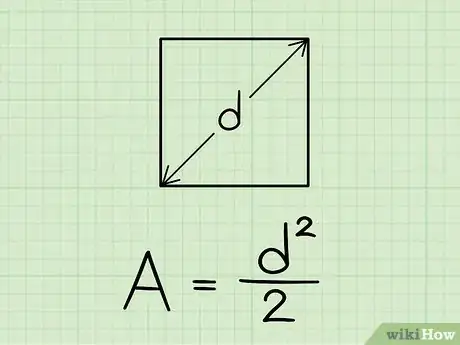
2Comprendi la formula per calcolare l'area di un quadrato partendo dalla diagonale. Area = (Diagonale^2)/2.
-
3Eleva al quadrato la misura della diagonale. Moltiplica il valore in tuo possesso per se stesso. Ipotizziamo che la diagonale del quadrato in esame misuri 5 cm. A questo punto elevalo al quadrato ottenendo: 5 x 5 = 25 cm2.
-
4Dividi per 2 il valore ottenuto nel passaggio precedente. Svolgendo i calcoli otterrai: 25 cm2 / 2 = 12,5 cm2. Complimenti, il tuo lavoro è completo.Pubblicità
Usare il Perimetro
-
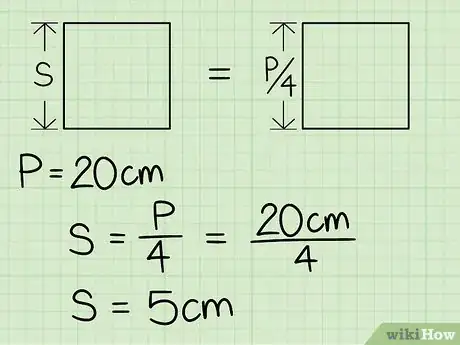
1Moltiplica la misura del perimetro per 1/4, in modo da individuare la lunghezza di un singolo lato. Questa operazione corrisponde a dividere il perimetro per il numero 4. Dato che il quadrato è un parallelogramma speciale, in cui tutti i lati sono uguali, partendo dal perimetro puoi risalire facilmente alla lunghezza dei lati dividendolo per 4. Ipotizza di lavorare su un quadrato che abbia il perimetro pari a 20 cm. Per calcolare il lato basta eseguire questa operazione: 20 x 1/4 = 5 cm. A questo punto sai che la lunghezza del lato del quadrato in esame è pari a 5 cm.
-
2Moltiplica il valore ottenuto nel passaggio precedente per se stesso elevandolo al quadrato. Adesso che sai che il lato della figura in esame è pari a 5 cm sei in grado di calcolare l'area utilizzando la formula standard: Area = (5 cm)2 = 25 cm2Pubblicità
Informazioni su questo wikiHow
Per calcolare l'area di un quadrato, usa la formula a = lxl, in cui l rappresenta la lunghezza di uno dei lati della figura. Se conosci solo il perimetro del quadrato, puoi trovare l'area dividendolo per quattro, in modo da ottenere la misura di un lato, poi utilizzare la stessa formula precedente, a = lxl. Se vuoi imparare a calcolare l'area di un quadrato conoscendo solo la lunghezza di una diagonale, continua a leggere!
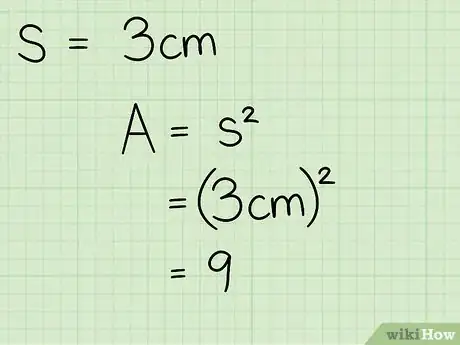



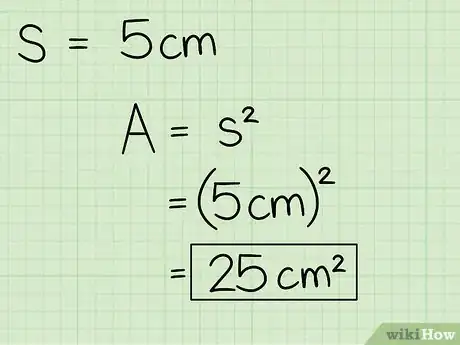




-to-Grams-(g)-Step-12-Version-4.webp)














