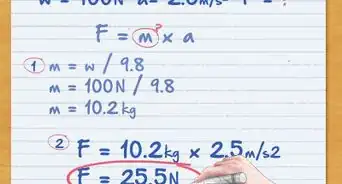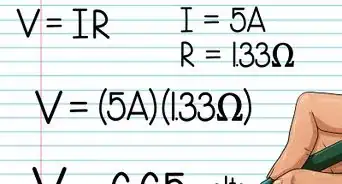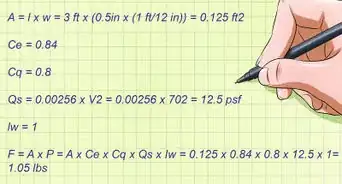Come Calcolare la Coppia di Torsione

Info sull'Autore

La coppia è meglio definita come la tendenza di una forza a far ruotare un oggetto attorno a un asse, fulcro o pivot. È possibile calcolare la coppia usando la forza e il braccio del momento (la distanza perpendicolare da un asse alla linea d'azione di una forza) o tramite il momento d'inerzia e l'accelerazione angolare.

Metodo 1

Metodo 1 di 2:

Utilizzare la Forza e il Braccio del Momento

1
Identifica le forze esercitate sul corpo e i corrispondenti bracci del momento. Se la forza non è perpendicolare al braccio del momento considerato (cioè è montata ad angolo), potrebbe essere necessario trovare le componenti usando le funzioni trigonometriche come seno o coseno.
- La componente della forza che consideri dipenderà dall'equivalente della forza perpendicolare.
- Immagina una barra orizzontale e applica una forza di 10N con un angolo di 30° sopra l'orizzontale per ruotare il corpo intorno al suo centro.
- Poiché devi utilizzare una forza che sia perpendicolare al braccio del momento, hai bisogno di una forza verticale per ruotare la barra.
- Pertanto, devi considerare la componente y o utilizzare F = 10 sin30° N.
2
Usa l'equazione per la coppia, τ = Fr in cui sostituire semplicemente le variabili con i dati ottenuti o che hai già.
- Un semplice esempio: immagina un bambino di 30 kg seduto all’estremità di un’altalena. La lunghezza dell'altalena è 1,5 m.
- Poiché l'asse di rotazione dell'altalena è al centro, non devi moltiplicare per la lunghezza.
- Devi determinare la forza esercitata dal bambino, utilizzando la massa e l’accelerazione.
- Poiché hai la massa, devi moltiplicarla per l'accelerazione di gravità, g, che è uguale a 9,81 m/s².
- Ora, hai tutti i dati necessari per utilizzare l'equazione della coppia:
3
Usa le convenzioni di segno (positivo o negativo) per mostrare la direzione della coppia. Quando la forza ruota il corpo in senso orario, la coppia è negativa. Quando lo ruota in senso antiorario, la coppia è positiva.
- Per più forze applicate, devi sommare tutte le coppie di torsione nel corpo.
- Poiché ogni forza tende a produrre rotazioni in diverse direzioni, l'uso convenzionale del segno è importante per tenere traccia di quali forze agiscono in quali direzioni.
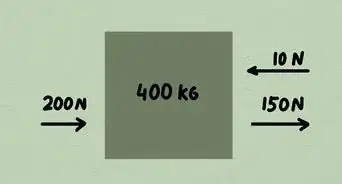
- Ad esempio, due forze F1 = 10,0 N in senso orario e F2 = 9,0 N in senso antiorario, sono applicate al bordo di una ruota di diametro 0,050 m.
- Poiché il corpo dato è un cerchio, il suo asse fisso è il centro. Devi dimezzare il diametro per ottenere il raggio. La misura del raggio servirà come braccio del momento. Quindi il raggio è pari a 0,025 m.
- Per chiarezza, possiamo risolvere per le singole coppie generate dalle forze.
- Per la forza 1, l'azione è in senso orario, quindi la coppia prodotta è negativa.
- Per la forza 2, l'azione è in senso antiorario, quindi la coppia prodotta è positiva.
- Ora possiamo solo sommare le coppie per ottenere la coppia risultante.
Pubblicità

Metodo 2

Metodo 2 di 2:

Utilizzare il Momento di Inerzia e l'Accelerazione Angolare

1
Cerca di capire come il momento d'inerzia del corpo funziona per iniziare a risolvere il problema. Il momento d'inerzia è la resistenza di un corpo al movimento rotatorio. Dipende dalla massa e anche da come è distribuita.
- Per capire questo con chiarezza, immagina due cilindri dello stesso diametro ma di masse diverse.
- Immagina di dover ruotare i due cilindri rispetto ai loro centri.
- Ovviamente, il cilindro con la massa maggiore sarà più difficile da ruotare rispetto all'altro, poiché è "più pesante".
- Ora immagina due cilindri con diametri diversi ma stessa massa. Appariranno ancora con la stessa massa, ma, allo stesso tempo, presentando diversi diametri, le forme o distribuzioni di massa di entrambi i cilindri differiranno.
- Il cilindro con un diametro maggiore sarà simile a una piastra piana e circolare, mentre il cilindro di diametro più piccolo sarà simile a un tubo di consistenza molto compatta.
- Il cilindro con un diametro maggiore sarà più difficile da ruotare, perché avrai bisogno di una forza maggiore per tenere conto del braccio del momento più lungo.
2
Scegli quale equazione utilizzare per trovare il momento d'inerzia. Ne esistono diverse.
- In primo luogo c’è la semplice equazione con la sommatoria della massa e i bracci del momento di ogni particella.
- Questa equazione è utilizzata per punti o particelle ideali. Un punto materiale è un oggetto che ha una massa, ma non occupa spazio.
- In altre parole, l’unica caratteristica rilevante dell'oggetto è la sua massa; non è necessario conoscere la sua dimensione, forma o struttura.
- Il concetto di punto materiale è comunemente usato in fisica per semplificare i calcoli e utilizzare scenari ideali e teorici.
- Ora, immagina oggetti come un cilindro cavo o una sfera uniformemente solida. Questi oggetti hanno forma, dimensione e struttura chiare e precise.
- Pertanto, non è possibile considerarli come un punto materiale.
- Per fortuna, è possibile utilizzare le equazioni disponibili che si applicano ad alcuni di questi oggetti comuni.
3
Trova il momento d'inerzia. Per iniziare a trovare la coppia, è necessario calcolare il momento d'inerzia. Utilizza il seguente problema di esempio:
- Due piccoli "pesi" di massa 5,0 e 7,0 kg sono montati agli estremi opposti di una barra luminosa lunga 4,0 m (la cui massa può essere trascurata). L'asse di rotazione è al centro dell'asta. L'asta viene ruotata a partire dallo stato di quiete con velocità angolare di 30,0 rad/s per 3,00 s. Calcolare la coppia prodotta.
- Poiché l'asse di rotazione è al centro, il braccio del momento di entrambi i pesi è uguale alla metà della lunghezza dell'asta, che è 2,0 m.
- Poiché non erano specificate forma, dimensione e struttura dei "pesi", possiamo supporre che siano particelle ideali.
- Il momento d'inerzia può essere calcolato come segue.
4
Trova l'accelerazione angolare, α. La formula, α = at / r, può essere utilizzata per calcolare l’accelerazione angolare.
- La prima formula, α = at / r, può essere utilizzata se si conoscono l'accelerazione tangenziale e il raggio.
- L'accelerazione tangenziale è l'accelerazione tangente al percorso del movimento.
- Immagina un oggetto lungo un percorso curvo. L'accelerazione tangenziale è semplicemente la sua accelerazione lineare in qualsiasi punto lungo il percorso.
- Per la seconda formula, il modo più semplice per illustrare questo concetto è di metterlo in relazione alla cinematica: spostamento, velocità lineare e accelerazione lineare.
- Lo spostamento è la distanza percorsa da un oggetto (unità SI: metro, m); la velocità lineare è il tasso di variazione dello spostamento nel tempo (unità di misura: m/s); l’accelerazione lineare è il tasso di variazione della velocità lineare nel tempo (unità di misura: m/s²).
- Ora, considera le controparti nel movimento rotatorio: lo spostamento angolare, θ, angolo di rotazione di un determinato punto o linea (unità SI: rad); la velocità angolare, ω, variazione di spostamento angolare nel tempo (unità SI: rad/s); l'accelerazione angolare, α, cambiamento della velocità angolare nell’unità di tempo (unità SI: rad/s²).
- Tornando al nostro esempio, ti sono stati forniti i dati per il momento angolare e il tempo. Dal momento che è partito da fermo, la velocità angolare iniziale è 0. Possiamo usare l'equazione seguente per il calcolo.
5
Usa l'equazione, τ = Iα, per trovare la coppia. Sostituisci semplicemente le variabili con le risposte ottenute dai passaggi precedenti.
- Puoi notare che l'unità "rad" non rientra nelle nostre unità, perché è considerata una quantità adimensionale, cioè priva di dimensioni.
- Questo significa che puoi non tener conto di essa e continuare con il calcolo.
- Per motivi di analisi dimensionale, possiamo esprimere l’accelerazione angolare nell'unità s^-2.
Pubblicità

Consigli

Nel primo metodo, se il corpo è un cerchio e l'asse di rotazione è il centro, non è necessario trovare le componenti della forza (a condizione che la forza non sia inclinata), poiché la forza giace sulla tangente del cerchio immediatamente perpendicolare al braccio del momento.
Se ti risulta difficile immaginare come si verifica la rotazione, utilizza la penna e cerca di ricreare il problema. Assicurati di copiare la posizione dell'asse di rotazione e la direzione della forza applicata per un'approssimazione più adeguata.