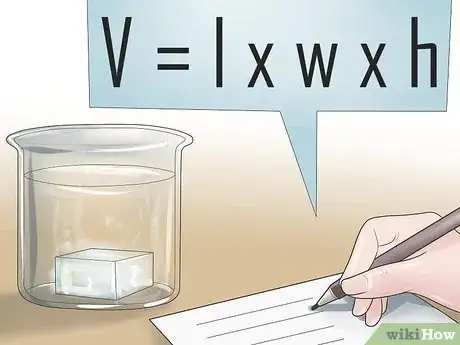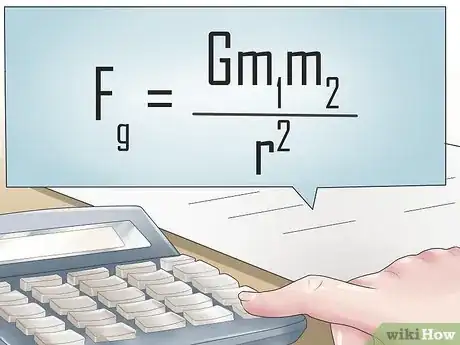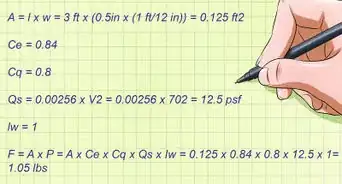Come Calcolare la Forza Idrostatica

La spinta idrostatica è una forza che agisce in senso opposto alla gravità su tutti gli oggetti immersi in un fluido. Il peso spinge l’oggetto sul fluido (liquido o gas) mentre il galleggiamento lo porta in alto, contrastando la gravità. In termini generali, la forza idrostatica può essere calcolata con la formula F_b = V_s × D × g, dove F_b è la forza idrostatica, V_s è il volume immerso, D è la densità del fluido in cui è posto l’oggetto e g è l’accelerazione di gravità. Per sapere come calcolare il galleggiamento di un oggetto, leggi questa guida.

Metodo 1

Metodo 1 di 2:

Usare la Formula della Spinta Idrostatica

1
Trova il volume della porzione immersa dell’oggetto. La forza idrostatica è direttamente proporzionale al volume sommerso dell’oggetto: più è immerso nel liquido, maggiore è la forza idrostatica che agisce su di esso. Tale azione si rileva su qualunque oggetto posto in un fluido, per cui il primo passo per calcolare tale forza dovrebbe sempre essere la valutazione di tale volume che, per questa formula, dovrebbe essere indicato in metri³.
- Per gli oggetti completamente immersi, tale volume equivale al volume dell’oggetto stesso. Per quelli che galleggiano sulla superficie, invece, bisogna considerare solo la parte sottostante.
- Come esempio, supponiamo di voler considerare la forza idrostatica di una palla di gomma in acqua. Se si tratta di una perfetta sfera del diametro 1 metro e se sta esattamente per metà fuori e per metà sotto l’acqua, possiamo trovare il volume immerso calcolando quello della palla intera e dividendolo per metà. Siccome il volume di una sfera è (4/3)π(raggio)³ , sappiamo che quello della nostra palla è (4/3)π(0,5)³ = 0,524 metri³. 0,524/2 = 0,262 metri³ NEL liquido.
2
Trova la densità del fluido. Il passo successivo nel procedimento per trovare la forza idrostatica è definire la densità (in chilogrammi/metri³) del liquido in cui è immerso l’oggetto. La densità è una misura relativa al peso di un oggetto o di una sostanza rispetto al suo volume. Dati due oggetti di uguale volume, quello con densità maggiore peserà di più. Come regola generale, maggiore è la densità del fluido in cui è immerso un oggetto, maggiore sarà la spinta idrostatica. Con i fluidi, di solito è più semplice trovarne la densità guardando semplicemente le tabelle riferite al materiale.
- Nel nostro esempio, la palla sta galleggiando in acqua. Consultando qualunque libro di testo, troviamo che la densità dell’acqua è circa 1.000 chilogrammo/metro³.
- Le densità di molti altri fluidi comuni sono riportate nelle tabelle tecniche. Un elenco di questo genere si trova qui.
3
Trova la forza dovuta alla gravità, cioè la forza peso (o qualunque altra forza tendente verso il basso). Sia che l’oggetto fluttui o sia completamente sommerso nel fluido, è sempre e comunque soggetto alla gravità. Nel mondo reale, questa costante vale circa 9,81 newton/chilogrammo. Inoltre, nelle situazioni in cui agisce un’altra forza, come quella centrifuga, bisogna considerare la forza totale che agisce verso il basso per l’intero sistema.
- Nel nostro esempio, se abbiamo a che fare con un semplice sistema statico, possiamo supporre che la sola forza che agisce verso il basso nell’oggetto posto nel fluido sia la gravità standard — 9,81 newton/chilogrammo.
- Comunque, che cosa accadrebbe se la nostra palla galleggiasse in un secchio d’acqua fatto girare a gran forza in cerchio orizzontalmente? In questo caso, assumendo che il secchio venga fatto ruotare abbastanza velocemente in modo che non escano né l’acqua né la palla, la forza che spinge verso il basso in questa situazione deriverebbe dalla forza centrifuga utilizzata per ruotare il secchio, non dalla gravità terrestre.
4
Moltiplica volume × densità × gravità. Quando conosci il volume dell’oggetto (in metri³), la densità del fluido (in chilogrammi/metri³) e la forza peso (o quella, nel tuo sistema, che spinge verso il basso), trovare la forza di galleggiamento è semplice. Basta moltiplicare le tre quantità per avere un risultato in newton.
- Risolviamo il nostro problema inserendo i valori trovati nell’equazione F_b = V_s × D × g. F_b = 0,262 metri³ × 1.000 chilogrammi/metri³ × 9,81 newton/chilogrammo = 2.570 newton.
5
Scopri se il tuo oggetto galleggia facendo una comparazione con la sua forza peso. Usando l’equazione appena vista, è facile trovare la forza con cui l’oggetto è spinto fuori dal liquido in cui è immerso. Inoltre, con qualche sforzo in più, puoi anche determinare se l’oggetto galleggerà oppure affonderà. Trova semplicemente la forza idrostatica per l’intero oggetto (in altre parole, usa tutto il suo volume come V_s), poi trova la forza peso con la formula G = (massa dell’oggetto)(9,81 metri/secondo²). Se la spinta idrostatica è superiore al peso, l’oggetto galleggerà. D’altra parte, se è inferiore, affonderà. Se sono uguali, si dice che l’oggetto “galleggia in maniera neutrale”.
- Per esempio, supponiamo di voler sapere se un barile cilindrico in legno di 20 kg con un diametro di 75 m e alto 1,25 m galleggerà in acqua. Questo studio richiederà diversi passaggi:
  - Possiamo trovare il suo volume con la formula del cilindro V = π(raggio)²(altezza). V = π(0,375)²(1,25) = 0,55 metri³.
  - Dopo di che, supponendo di essere sotto l’azione di comune gravità e di avere acqua di densità solita, possiamo calcolare la forza idrostatica sul barile. 0,55 metri³ × 1000 chilogrammi/metro³ × 9,81 newton/chilogrammo = 5.395,5 newton.
  - A questo punto, dovremo trovare la forza di gravità agente sul barile (la sua forza peso). G = (20 kg)(9,81 metri/secondo²) = 196,2 newton. Quest’ultima è di gran lunga inferiore alla forza di galleggiamento, per cui il barile galleggerà.
6
Usa lo stesso approccio quando il fluido è un gas. Quando si tratta di fluidi, non è detto che si tratti di un liquido. I gas vengono trattati come fluidi e, sebbene la loro densità sia molto bassa rispetto a quella di altri tipi di materia, possono comunque supportare certi oggetti che fluttuano dentro di loro. Un pallone riempito d’elio è un tipico esempio. Essendo tale gas meno denso del fluido che lo circonda (l’aria), esso fluttua!

Pubblicità

Metodo 2

Metodo 2 di 2:

Eseguire un Semplice Esperimento di Galleggiamento

1
Metti una tazzina o una piccola coppa dentro una più grande. Con pochi oggetti casalinghi, è facile osservare i principi idrostatici in azione! In questo semplice esperimento, dimostreremo che un oggetto in superficie è sottoposto a galleggiamento perché sposta un volume di liquido pari al volume dell’oggetto sommerso. Riusciremo anche a dimostrare con questo esperimento come trovare praticamente la forza idrostatica di un oggetto. Per iniziare, metti una ciotola o una tazza all’interno di un contenitore più grande, come un catino o un secchio.
2
Riempi il contenitore fino all’orlo. Successivamente, riempi d’acqua il contenitore più piccolo interno. Il livello dell’acqua deve arrivare fino all’orlo senza che fuoriesca. Fai molta attenzione a questo punto! Se versi dell’acqua, svuota il contenitore più largo prima di riprovare.
- Ai fini di questo esperimento, è lecito ritenere che l’acqua abbia una densità standard di 1.000 chilogrammi/metro³. A meno che non si utilizzi acqua salata o un liquido completamente diverso, la maggior parte dei tipi di acqua avrà una densità abbastanza vicina a questo valore di riferimento tanto che qualche differenza infinitesima non cambierà i nostri risultati.
- Se hai un contagocce a portata di mano, potrà essere molto utile per livellare precisamente l’acqua nel contenitore interno.
3
Immergi un piccolo oggetto. A questo punto, trova un piccolo oggetto che possa adattarsi all'interno del contenitore interno senza essere danneggiato dall'acqua. Trova la massa di questo oggetto in chilogrammi (è meglio utilizzare una bilancia o un bilanciere che possa darti i grammi che convertirai in chili). Poi, senza lasciare che le dita si bagnino, immergilo in acqua lentamente e costantemente fino a quando non inizia a galleggiare o riesci a trattenerlo, poi lascialo andare. Dovresti notare un po’ d’acqua che fuoriesce dal bordo del contenitore interno cadendo all’esterno.
- Ai fini del nostro esempio, supponiamo di immergere una macchinina giocattolo della massa di 0,05 chili nel contenitore interno. Non è necessario conoscere il volume di questa automobilina per calcolare il galleggiamento, come vedremo nel prossimo passaggio.
4
Raccogli e misura l’acqua che si riversa. Quando si immerge un oggetto nell’acqua, si sposta del liquido; se non accade, significa che non c’è spazio per entrare in acqua. Quando si spinge contro il liquido, esso risponde spingendo a propria volta, dando luogo al galleggiamento. Prendi l’acqua traboccata dal contenitore interno e versala in un misurino di vetro. Il volume dell’acqua nella tazza deve essere uguale a quello della porzione dell’oggetto sommerso.
- In altri termini, se il tuo oggetto galleggia, il volume dell’acqua che trabocca sarà uguale al volume dell’oggetto immerso sotto la superficie dell’acqua. Se affonda, il volume d’acqua versato sarà uguale al volume dell’intero oggetto.
5
Calcola il peso dell’acqua fuoriuscita. Poiché conosci la densità dell'acqua e puoi misurare il volume dell'acqua che hai versato nel misurino, puoi trovare la sua massa. Converti semplicemente questo volume in metri³ (uno strumento di conversione online, come questo, può venire in aiuto) e moltiplicalo per la densità dell’acqua (1.000 chilogrammi/metri³).
- Nel nostro esempi, supponiamo che la nostra macchinina affondi nel contenitore interno e sposti circa due cucchiaini d’acqua (0,00003 metri³). Per trovare la massa dell'acqua, dobbiamo moltiplicarla per la sua densità: 1.000 chilogrammi/metri³ × 0,00003 metri³ = 0,03 chilogrammi.
6
Confronta la massa dell’acqua spostata con quella dell’oggetto. Ora che conosci la massa dell’oggetto immerso in acqua e quella dell’acqua spostata, fai un paragone per vedere quale sia maggiore. Se la massa dell’oggetto immerso nel contenitore interno è maggiore di quella spostata, dovrebbe affondare. D’altra parte, se la massa dell’acqua spostata è maggiore, l’oggetto dovrebbe rimanere in superficie. Questo è il principio della spinta idrostatica in azione — perché un oggetto possa galleggiare, esso deve spostare un volume di acqua di massa superiore a quella dell’oggetto stesso.
- Così, gli oggetti con masse piccole ma con grandi volumi sono quelli che tendono maggiormente a rimanere in superficie. Questa proprietà significa che gli oggetti cavi tendono a galleggiare. Pensa a una canoa: fluttua bene perché è cava all’interno, così è capace di spostare molta acqua anche senza avere una massa molto elevata. Se le canoe fossero solide, non galleggerebbero certo bene!
- Nel nostro esempio, l’automobilina ha una massa superiore (0,05 chilogrammi) a quella dell’acqua (0,03 chilogrammi). Questo conferma quanto osservato: la macchinina affonda.
Pubblicità