Questo articolo è stato co-redatto da Grace Imson, MA. Grace Imson è un'insegnante di matematica con oltre 40 anni di esperienza. Grace è attualmente docente di matematica presso il City College of San Francisco e ha lavorato in precedenza nel Dipartimento di Matematica della Saint Louis University. Oltre all'università, ha insegnato matematica alle scuole elementari, medie e superiori. Ha conseguito la Laurea Magistrale in Educazione, con specializzazione in Amministrazione e Supervisione, presso la Saint Louis University.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 8 653 volte
La pendenza di una retta, a cui si fa riferimento anche con il termine coefficiente angolare, ne misura l'inclinazione.[1] Si tratta del rapporto fra lo "scostamento verticale" e lo "scostamento orizzontale", cioè il rapporto della variazione verticale della retta rispetto alla variazione lungo l'asse orizzontale. Essere in grado di calcolare il coefficiente angolare di una retta (o la pendenza) oppure di individuare i punti di intersezione con gli assi X e Y sfruttando questa informazione è un'abilità molto importante in ambito economico [2] , scientifico[3] , finanziario e in molti altri settori.
Passaggi
Calcolare la Pendenza di una Retta Graficamente
-
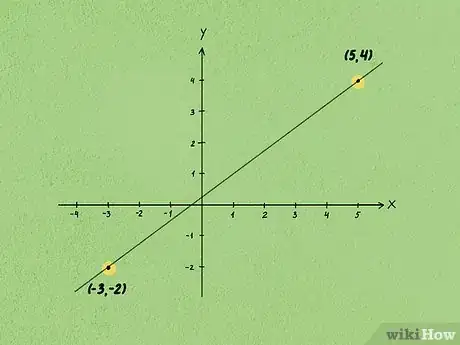
1Scegli due punti appartenenti alla retta in esame. Riportali sul grafico cartesiano in cui è presente la retta e prendi nota delle coordinate.
- Quando si disegna un punto su un grafico cartesiano, bisogna indicarne sempre le coordinate X e Y.
- Per esempio, ipotizziamo di aver scelto i seguenti punti: (-3, -2) e (5, 4).
-
2Calcola lo scostamento verticale esistente fra i due punti presi in esame. In questo caso, occorre semplicemente calcolare la differenza esistente fra le coordinate dell'asse Y dei due punti. Inizia prendendo in esame il punto che si trova più a sinistra sul grafico, quindi misura la distanza che lo separa dal secondo punto lungo l'asse delle ordinate.
- La variazione lungo l'asse Y può essere sia positiva sia negativa, quindi per misurarla dovrai muoverti rispettivamente verso l'alto o verso il basso.[4] Se la retta passa nel quadrante superiore destro del piano cartesiano, significa che la misura dello scostamento verticale sarà positiva, mentre se passa nel quadrante inferiore destro sarà negativa.[5]
- Per esempio, se la coordinata Y del primo punto è (-2) e la coordinata Y del secondo punto è (4), la differenza sarà pari a 6 unità, quindi lo scostamento verticale sarà pari a 6.
-
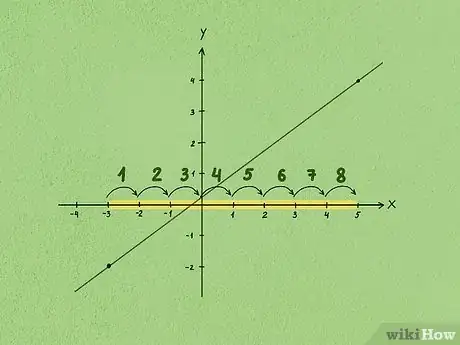
3Calcola lo scostamento orizzontale esistente fra i due punti presi come esempio. In questo caso, occorre calcolare semplicemente la differenza esistente fra le coordinate dell'asse X dei due punti. Inizia prendendo in esame il punto che si trova più a sinistra sul grafico, quindi misura la distanza che lo separa dal secondo punto lungo l'asse delle ascisse.
- In questo caso la variazione lungo l'asse X è sempre positiva, quindi per effettuare la misurazione dovrai muoverti sempre da sinistra verso destra e non viceversa.[6]
- Per esempio, se la coordinata X del primo punto è (-3) e quella del secondo punto è (5), la differenza esistente sarà pari a 8 unità, quindi lo scostamento orizzontale sarà 8.
-
4Per determinare la pendenza della retta studiata, calcola il rapporto dello scostamento verticale rispetto a quello orizzontale. Normalmente, il coefficiente angolare viene presentato sotto forma di frazione, ma può anche trattarsi di un numero intero.
- Nel nostro esempio, abbiamo calcolato che lo scostamento verticale fra i due punti è di 6 unità, mentre quello orizzontale è di 8 unità, quindi la pendenza della retta in esame sarà pari a che semplificando dà come risultato finale .
Pubblicità
Calcolare la Pendenza di una Retta Usando Due Punti
-
1Dati due punti, per calcolare il coefficiente angolare di un retta si usa la seguente formula matematica: . La variabile m rappresenta il coefficiente angolare, la coppia di valori rappresenta le coordinate cartesiane del primo punto, mentre la coppia di valori rappresenta le coordinate cartesiane del secondo punto.
- È bene ricordare che il coefficiente angolare di una retta è pari al seguente rapporto: . Per calcolare la variazione lungo l'asse Y (scostamento verticale) e la variazione lungo l'asse X (scostamento orizzontale) utilizziamo la formula matematica indicata.[7]
-
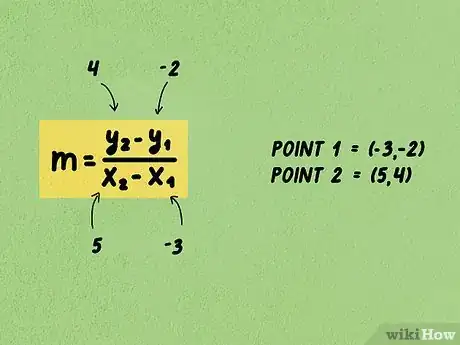
2Sostituisci le variabili della formula con le coordinate X e Y dei due punti conosciuti. Assicurati di sostituire i valori () con le rispettive coordinate del primo punto, mentre i valori () con le coordinate del secondo punto. In caso contrario, non sarai in grado di calcolare la pendenza.
- Per esempio, ipotizzando di analizzare i punti cartesiani (-3, -2) e (5, 4), la formula dovrebbe apparire come segue: .
-
3Adesso completa i calcoli ed esegui le semplificazioni necessarie ove possibile. In questo modo, otterrai il coefficiente angolare della retta studiata che sarà rappresentato da una frazione o da un numero intero.
- Nel nostro esempio, la formula è . Eseguendo i calcoli al numeratore, otterremo (ricorda che sottraendo un numero negativo in realtà si deve eseguire la somma), mentre al denominatore otterremo . Arrivati a questo punto, è possibile semplificare la frazione in , quindi possiamo affermare che il coefficiente angolare della retta studiata è pari a .
Pubblicità
Calcolare il Punto di Intersezione con l'Asse Y Utilizzando il Coefficiente Angolare e un Punto
-
1Per effettuare questa operazione faremo riferimento all'equazione . In questa formula, la variabile y rappresenta l'ordinata di un punto qualunque appartenente alla retta studiata, la variabile m è il coefficiente angolare (che rappresenta la pendenza della retta), la variabile x rappresenta l'ascissa di un punto qualunque appartenente alla retta e la variabile b rappresenta il punto di intersezione con l'asse Y del piano cartesiano.
- La formula rappresenta l'equazione di una retta.[8]
- La variabile b rappresenta la coordinata Y del punto di intersezione della retta con l'asse delle ordinate del piano cartesiano.
Consiglio dell'EspertoGrace Imson è un'insegnante di matematica con oltre 40 anni di esperienza. Grace è attualmente docente di matematica presso il City College of San Francisco e ha lavorato in precedenza nel Dipartimento di Matematica della Saint Louis University. Oltre all'università, ha insegnato matematica alle scuole elementari, medie e superiori. Ha conseguito la Laurea Magistrale in Educazione, con specializzazione in Amministrazione e Supervisione, presso la Saint Louis University.Insegnante di Matematica al City College of San Francisco
 Grace Imson, MA
Grace Imson, MA
Insegnante di Matematica al City College of San FranciscoL'Esperto Concorda: Se hai una pendenza e un punto, inserisci i dati in un'equazione. Sapendo che y = mx + b, dove m è la pendenza, x e y sono le coordinate della retta, non resta che risolvere l'equazione per b per trovare il punto d'intersezione della retta.
-
2Sostituiamo le variabili note dell'equazione con i rispettivi valori. Ricorda che il coefficiente angolare di una retta ne indica la pendenza, cioè il rapporto fra lo scostamento verticale e quello orizzontale. Se hai la necessità di scoprire come si calcola il coefficiente angolare di una retta, fai riferimento ai metodi precedenti dell'articolo.
- Per esempio, ipotizziamo che il coefficiente angolare della retta sia e che quest'ultima passi per il punto (5,4). In questo scenario, l'equazione che descrive la retta sarà la seguente: .
-
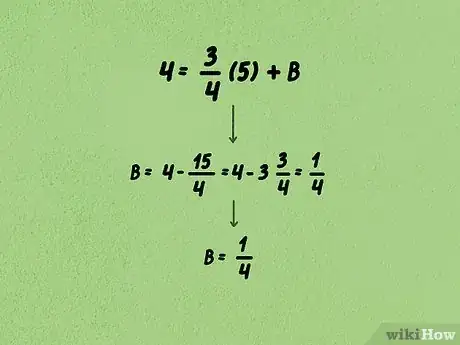
3Risolviamo l'equazione in base alla variabile b. Per prima cosa, moltiplichiamo il coefficiente angolare per l'ascissa del punto dato. A questo punto sottraiamo il prodotto ottenuto da entrambi i membri dell'equazione e risolviamo quest'ultima in base alla variabile b.
- Nel nostro esempio, dopo la sostituzione dei valori noti, abbiamo ottenuto la seguente equazione: . Procediamo con la sottazione del termine da entrambi i membri dell'equazione, ottenendo: . A questo punto, possiamo affermare che la retta studiata interseca l'asse Y nel punto .
-
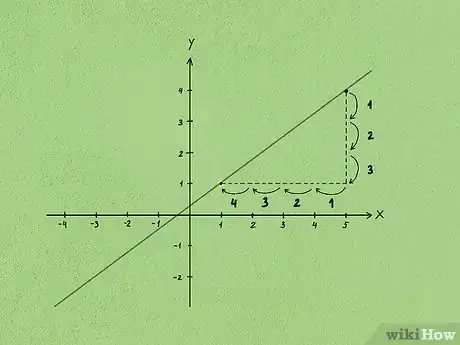
4Verifica la correttezza dei calcoli. Disegna il punto dato all'interno di un piano cartesiano, quindi utilizza il coefficiente angolare per tracciare la relativa retta. Adesso, esamina il punto in cui la retta tracciata interseca l'asse Y e verifica che l'ordinata del punto di intersezione sia pari al valore ottenuto dai calcoli.
- Nel nostro esempio, il coefficiente angolare della retta studiata è e quest'ultima passa anche per il punto (5,4). Procedi riportando il punto dato su un piano cartesiano, quindi individua un secondo punto appartenete alla retta utilizzando il coefficiente angolare noto, cioè spostandoti dal primo punto di 3 unità verso sinistra e 4 unità verso il basso. Tracciando la retta che passa dai due punti individuati, quest'ultima dovrebbe passare anche nella parte superiore dell'origine del piano cartesiano, cioè il punto (0,0).
Pubblicità
Calcolare il Punto di Intersezione con l'Asse X Utilizzando il Coefficiente Angolare e il Punto di Intersezione con l'Asse Y
-
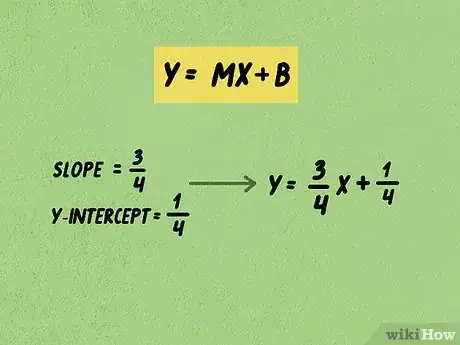
1Per effettuare questa operazione faremo riferimento all'equazione . In questa formula, la variabile y rappresenta l'ordinata di un punto qualunque appartenente alla retta studiata, la variabile m è il coefficiente angolare (che rappresenta la pendenza della retta), la variabile x rappresenta l'ascissa di un punto qualunque appartenente alla retta e la variabile b rappresenta il punto di intersezione con l'asse Y del piano cartesiano.
- La formula rappresenta l'equazione di una retta.[9]
- Il punto di intersezione dell'asse X è il punto del piano cartesiano in cui la retta taglia l'asse delle ascisse.
-
2Sostituiamo le variabili note dell'equazione con i rispettivi valori. Ricorda che il coefficiente angolare di una retta ne indica la pendenza, cioè il rapporto fra lo scostamento verticale e quello orizzontale. Se hai la necessità di scoprire come si calcola il coefficiente angolare di una retta, fai riferimento ai metodi precedenti dell'articolo.
- Per esempio, ipotizziamo che il coefficiente angolare della retta presa in esame sia e che quest'ultima tagli l'asse delle ordinate nel punto (0,). In questo scenario, l'equazione che descrive la retta sarà la seguente: .
-
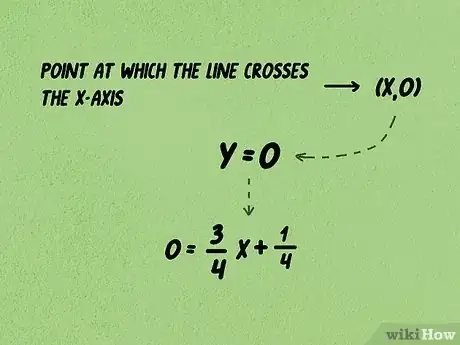
3Imposta la variabile y a 0.[10] Possiamo eseguire questo passaggio proprio perché stiamo cercando il punto di intersezione della retta con l'asse X, quindi l'ordinata di tale punto sarà pari a zero. Impostando la variabile y a 0 e risolvendo l'equazione ottenuta in base alla variabile x, otterremo esattamente ciò che stiamo cercando, cioè il punto (x, 0) che rappresenta il punto di intersezione della retta con l'asse X del piano cartesiano.
- Proseguendo con il nostro esempio, otterremo la seguente equazione: .
-
4Risolvi l'equazione in base alla variabile x. Per prima cosa, occorre sottrarre il valore della variabile y dell'equazione da entrambi i membri, quindi bisogna dividere questi ultimi per il coefficiente angolare.
- Nel nostro problema di esempio, otterremo la seguente equazione: . Dividendo entrambi i membri dell'equazione per , otterremo come risultato . Eseguendo le dovute semplificazioni, otterremo questa equazione: . A questo punto, possiamo affermare che la retta interseca l'asse X del piano cartesiano nel punto .
-
5Verifica la correttezza dei calcoli. Disegna il punto dato all'interno di un piano cartesiano, quindi utilizza il coefficiente angolare per tracciare la relativa retta. Adesso, esamina il punto in cui la retta tracciata interseca l'asse X e verifica che l'ascissa del punto di intersezione sia pari al valore ottenuto dai calcoli.
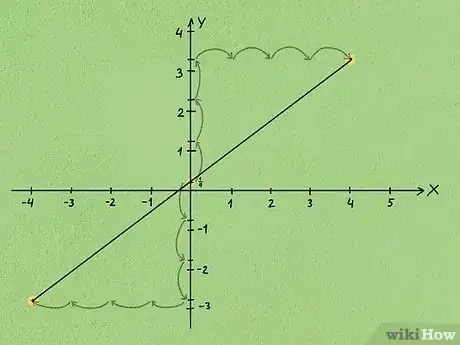
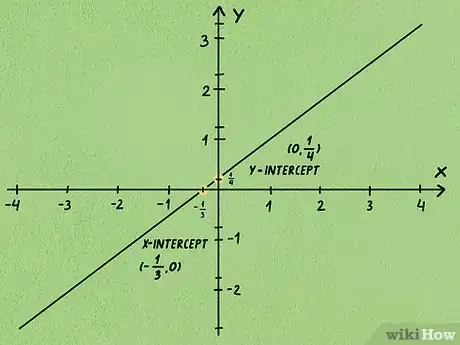
- Nel nostro esempio, il coefficiente angolare della retta studiata è e quest'ultima taglia l'asse Y nel punto . Procedi riportando il punto dato su un piano cartesiano, quindi individua altri due punti appartenenti alla retta utilizzando il coefficiente angolare noto, cioè spostandoti dal punto di intersezione con l'asse Y di 3 unità verso sinistra e 4 unità verso il basso prima e di 3 unità verso destra e di 4 unità verso l'alto dopo. Adesso, tracciando la retta che passa per tutti i punti disegnati, quest'ultima dovrebbe passare sulla sinistra dell'origine del piano cartesiano cioè il punto (0,0).
-
6Immagine finale relativa agli esempi.Pubblicità
Riferimenti
- ↑ http://www.mathopenref.com/coordslope.html
- ↑ http://www.columbia.edu/itc/sipa/math/slope_linear.html
- ↑ http://serc.carleton.edu/mathyouneed/slope/slopes.html
- ↑ http://www.coolmath.com/algebra/08-lines/05-finding-slope-line-from-graph-01
- ↑ http://www.mathopenref.com/coordslope.html
- ↑ http://www.coolmath.com/algebra/08-lines/05-finding-slope-line-from-graph-01
- ↑ http://www.coolmath.com/algebra/08-lines/06-finding-slope-line-given-two-points-01
- ↑ http://www.mathopenref.com/coordequation.html
- ↑ http://www.mathopenref.com/coordequation.html
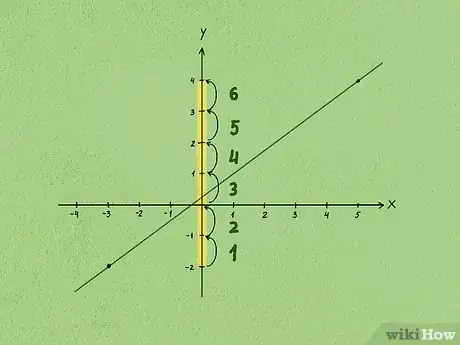
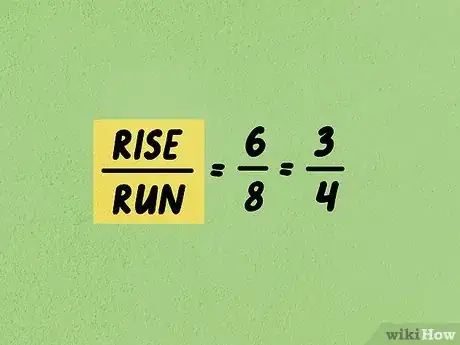


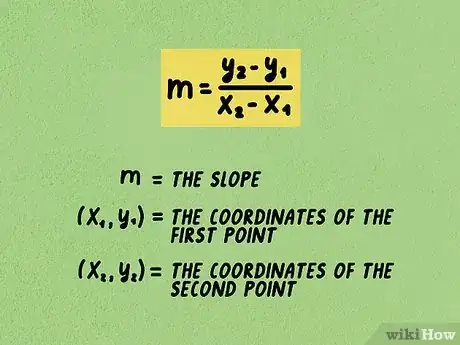





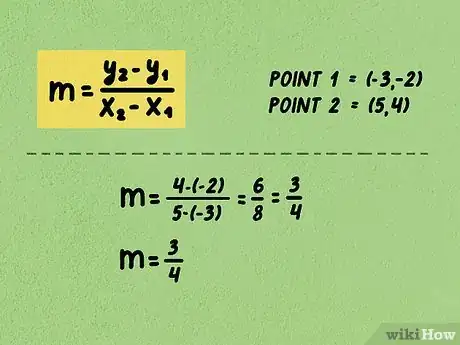





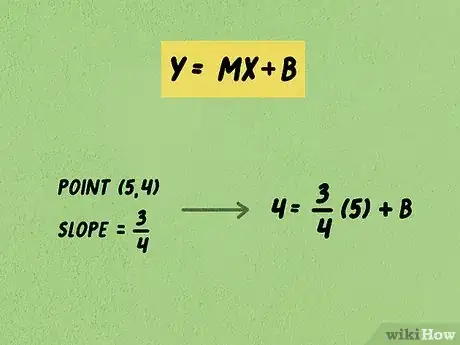









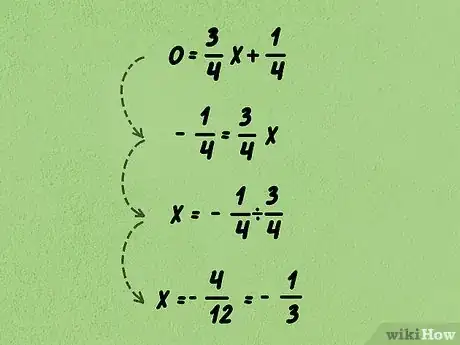







-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
