wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 18 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 23 543 volte
Le derivate possono essere utilizzate per ottenere le caratteristiche più interessanti di un grafico, come ad esempio i massimi, i minimi, i picchi, le valli e le pendenze. È persino possibile disegnare equazioni complesse senza una calcolatrice grafica! Purtroppo, ottenere la derivata è spesso noioso, ma questo articolo ti aiuterà con alcuni consigli e trucchi.
Passaggi
-
1Cerca di capire la notazione della derivata. Le due seguenti notazioni sono le più comuni, anche se ne esistono innumerevoli altre:
- Notazione di Leibniz: questa notazione è più comune quando l'equazione coinvolge y e x.
dy / dx significa letteralmente "la derivata di y rispetto a x". Può essere utile pensare alla derivata come Δy / Δx per valori di x e y che sono infinitesimamente diversi gli uni dagli altri. Questa spiegazione si presta per la definizione di limite di una derivata:
lim h->0 (f(x+h) - f(x)) / h.
Quando utilizzi questa notazione per la derivata seconda, devi scrivere:
dy2 / dx2. - Notazione di Lagrange: la derivata di una funzione f è scritta anche come f '(x). Questa notazione si pronuncia "f primo di x". Questa notazione è più breve di quella di Leibniz ed è utile quando si cerca la derivata di una funzione. Per formare le derivate di ordine superiore, basta aggiungere un altro segno " ' " e così la derivata seconda diventa f " (x).
- Notazione di Leibniz: questa notazione è più comune quando l'equazione coinvolge y e x.
-
2Cerca di comprendere che cosa è la derivata e perché viene utilizzata. Prima di tutto, per trovare la pendenza di un grafico lineare, si prendono due punti sulla linea e le loro coordinate che vanno inserite nell'equazione (y2 - y1) / (x2 -x1). Tuttavia, questa può essere utilizzata solo con grafici lineari. Per le equazioni quadratiche e di grado superiore, la linea è curva, quindi non è accurato prendere la "differenza" dei due punti. Al fine di trovare la pendenza della tangente di un grafico a curva, si prendono due punti e li si collega con l'equazione standard per trovare la pendenza del grafico di una curva: [f (x + dx) - f (x)] / dx. DX sta per "delta x", che è la differenza tra le due coordinate x dei due punti del grafico. Si noti che questa equazione è la stessa di (y2 - y1) / (x2 - x1), ma è solo in una forma diversa. Dal momento che è già noto che il risultato sarà impreciso, viene applicato un approccio indiretto. Per trovare la pendenza della tangente nel punto generico di coordinate (x, f(x)), dx deve avvicinarsi a 0, in modo che i due punti che sono stati presi si "fondano" in un unico punto. Tuttavia non è possibile dividere per 0, così, dopo aver sostituito i valori delle coordinate dei due punti, sarà necessario utilizzare la fattorizzazione e altri metodi per semplificare il dx al denominatore dell'equazione. Una volta fatto, imposta dx tendente a 0 e risolvi. Questa è la pendenza della tangente nel punto di coordinate (x, f(x)). La derivata di un'equazione è l'equazione generica per trovare la pendenza o coefficiente angolare di qualsiasi retta tangente a un grafico. Questo può sembrare molto complicato, ma ci sono alcuni esempi qui sotto, che aiuteranno a chiarire come ottenere la derivata.Pubblicità
Derivazione Esplicita
-
1Utilizza la derivazione esplicita quando l'equazione già ha y su un lato dell’uguaglianza.
-
2Inserisci l'equazione della formula [f (x + dx) - f (x)] / dx. Ad esempio, se l'equazione è y = x2, la derivata diventa [(x + dx) 2 - x2] / dx.
-
3Moltiplica e poi raccogli dx per formare l'equazione [dx (2 x + dx)] / dx. Ora è possibile semplificare dx tra numeratore e denominatore. Il risultato è 2 x + dx e, quando dx tende a 0, la derivata è 2x. Questo significa che la pendenza di ogni tangente del grafico y = x 2 è 2x. Basta sostituire il valore di x con l’ascissa del punto in cui si desidera trovare la pendenza.
-
4Impara degli schemi per derivare equazioni di tipo simile. Di seguito ce ne sono alcuni.
- La derivata di qualsiasi potenza è il denominatore della potenza moltiplicato per x elevato al valore di potenza meno 1. Ad esempio, la derivata di x5 è 5x4 e la derivata di x3,5 è 3,5x2,5. Se c'è già un numero davanti alla x, basta moltiplicarlo per l'esponente della potenza. Ad esempio, la derivata di 3x4 è 12x3.
- La derivata di una costante è zero. Così la derivata di 8 è 0.
- La derivata di una somma è la somma delle sue singole derivate. Ad esempio, la derivata di x3 + 3x2 è 3x2 + 6x.
- La derivata di un prodotto è la derivata del primo fattore per il secondo più la derivata del secondo per il primo. Ad esempio la derivata di x3(2 x + 1) è x3(2) + (2 x + 1)3x2, pari a 8x3 + 3x2.
- E infine la derivata di un quoziente (cioè f / g) è [g(derivata di f) - f(derivata di g)] / g2. Ad esempio la derivata di (x2 + 2x - 21) / (x - 3) è (x2 - 6x + 15) / (x - 3)2.
Pubblicità
Derivazione Implicita
-
1Utilizza la derivazione implicita quando l'equazione non può essere scritta facilmente con y su un lato solo dell’uguaglianza. Persino se tu fossi riuscito a scrivere con y su un lato, il calcolo di dy / dx sarebbe noioso. Di seguito è riportato un esempio di come si potrebbe risolvere questo tipo di equazione.
-
2In questo esempio, x2y + 2y3 = 3x + 2y, sostituisci y con f(x), così ti ricorderai che y è in realtà una funzione. Quindi l'equazione diventa x[f(x)]2 + 2[f(x)]3 = 3x + 2f(x).
-
3Per trovare la derivata di questa equazione, differenzia (una parolona per trovare la derivata) entrambi i lati dell'equazione rispetto a x. Quindi l'equazione diventa x2f '(x) + 2xf(x) + 6[f(x)]2f '(x) = 3 + 2f '(x).
-
4Sostituisci f (x) nuovamente con y. Fai attenzione a non fare lo stesso con f '(x), che è diverso da f(x).
-
5Risolvi per f '(x). La risposta di questo esempio viene (3 - 2xy) / (x 2 + 6y 2 - 2).Pubblicità
Consigli
- La derivata di yz (dove y e z sono entrambe le funzioni) non è semplicemente 1, perché y e z sono funzioni separate. Utilizza la regola del prodotto: yz = y(1) + z(1) = y + z.
- Pratica la regola del prodotto, la regola del quoziente, la regola della catena e soprattutto della derivazione implicita, in quanto queste sono di gran lunga le più difficili nell’analisi differenziale.
- Ogni volta che vedi un enorme problema da risolvere, non ti preoccupare. Basta provare a romperlo in piccolissimi pezzi applicando le norme di prodotto, quoziente ecc. Poi deriva le singole parti.
- Cerca di conoscere bene la tua calcolatrice: prova diverse funzioni della tua calcolatrice per imparare come usarle. E’ particolarmente utile sapere come utilizzare la tangente e le funzioni di derivata della tua calcolatrice, se esistono.
- Memorizza le derivate di base della trigonometria e impara come manipolarle.
Avvertenze
- Non dimenticare il segno meno davanti a f per derivata di g quando si utilizza la regola del quoziente: è un errore comune e dimenticarlo ti darà la risposta sbagliata!

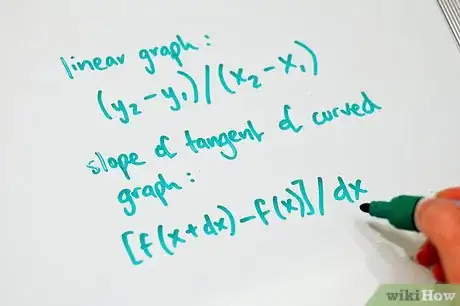


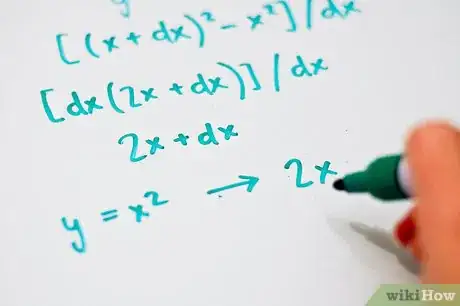
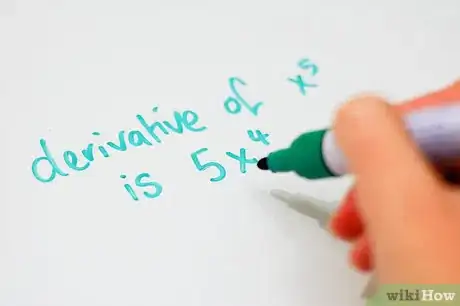



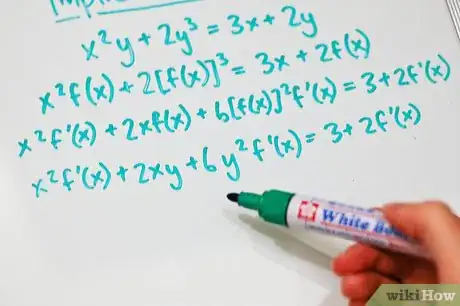
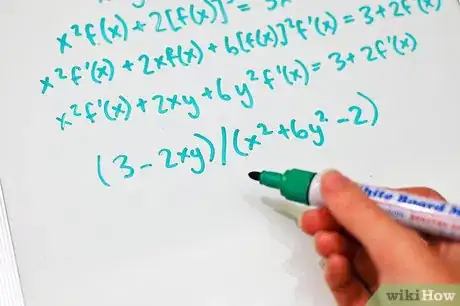






-to-Grams-(g)-Step-12-Version-4.webp)













