In un corso sulle equazioni differenziali si fa uso delle derivate studiate in un corso di analisi. La derivata è la misura di quanto cambia una quantità al variare di una seconda; per esempio, di quanto cambia la velocità di un oggetto rispetto al tempo (in confronto alla pendenza). Simili misure di cambiamento avvengono frequentemente nella vita di tutti i giorni. Per esempio, la legge dell'interesse composto afferma che la velocità dell'accumulo d’interesse è proporzionale al capitale iniziale, data da dy/dt=ky, dove y è la somma dell'interesse composto del denaro guadagnato, t è il tempo, e k è una costante (dt è un intervallo istantaneo di tempo). Sebbene, generalmente, l'interesse della carta di credito sia composto giornalmente e riportato come APR, tasso percentuale annuo, un’equazione differenziale può essere risolta per dare la soluzione istantanea y = ce^(kt), dove c è una costante arbitraria (il tasso d’interesse fisso). Quest'articolo ti mostrerà come risolvere delle comuni equazioni differenziali, soprattutto in meccanica e fisica.
Indice
Passaggi
Le basi
-
1Definizione di derivata. La derivata (anche indicata come quoziente differenziale, soprattutto nell’inglese britannico) è definita come il limite del rapporto tra l'incremento di una funzione(generalmente y)e l'incremento di una variabile(di solito x)in quella funzione, al tendere a 0 di quest'ultima; il cambiamento istantaneo di una quantità rispetto a un'altra, tipo la velocità, che è il cambiamento istantaneo della distanza rispetto al tempo. Confronta la prima derivata e la seconda derivata:
- Prima derivata - la derivata di una funzione, esempio: La velocità è la prima derivata della distanza rispetto al tempo.
- Seconda derivata - la derivata della derivata di una funzione, esempio: L'accelerazione è la seconda derivata della distanza rispetto al tempo.
-
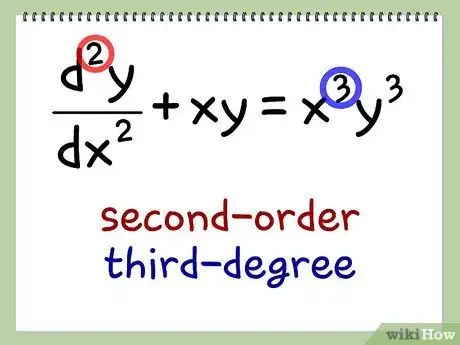
2Identifica l'ordine e il grado dell’equazione differenziale. L'ordine di un’equazione differenziale è determinato dalla derivata di ordine più alto; il grado è dato dalla potenza più alta di una variabile. Per esempio, l’equazione differenziale mostrata in Figura 1 è di secondo ordine e terzo grado.
-
3Impara la differenza tra una soluzione generale o completa e una soluzione particolare. Una soluzione completa contiene un numero di costanti arbitrarie pari all'ordine dell’equazione. Per risolvere un’equazione differenziale di ordine n, devi calcolare n integrali e per ogni integrale devi introdurre una costante arbitraria. Per esempio, nella legge d’interesse composto, l’equazione differenziale dy/dt=ky è di primo ordine e la sua soluzione completa y = ce^(kt) contiene esattamente una costante arbitraria. Si ottiene una soluzione particolare assegnando valori particolari alle costanti nella soluzione generale.Pubblicità
Risoluzione di Equazioni Differenziali di 1° Ordine
E' possibile esprimere un’equazione differenziale di primo ordine e primo grado nella forma M dx + N dy = 0, dove M e N sono funzioni di x e y. Per risolvere questa equazione differenziale, procedi come descritto qui di seguito:
-
1Verifica se le variabili sono separabili. Le variabili sono separabili se l’equazione differenziale può essere espressa come f(x)dx + g(y)dy = 0, dove f(x) è una funzione della sola x, e g(y) è una funzione della sola y. Queste sono le equazioni differenziali più facili da risolvere. Possono essere integrate a dare ∫f(x)dx + ∫g(y)dy = c, dove c è una costante arbitraria. Segue un approccio generale. Si veda la Figura 2 per un esempio.
- Elimina le frazioni. Se l’equazione contiene delle derivate, moltiplica per il differenziale della variabile indipendente.
- Raccogli in un solo termine tutti i termini contenenti lo stesso differenziale.
- Integra ciascuna parte separatamente.
- Semplifica l’espressione, per esempio, combinando i termini, convertendo i logaritmi in esponenti e usando il simbolo più semplice per le costatanti arbitrarie.
-
2Se le variabili non possono essere separate, verifica se si tratta di un’equazione differenziale omogenea. Un’equazione differenziale M dx + N dy = 0, è omogenea se la sostituzione di x e y con λx e λy risulta nella funzione originale moltiplicata per una potenza di λ, dove la potenza di λ è definita come il grado della funzione originale. Se questo è il tuo caso, segui i passaggi seguenti. Si veda la Figura 3 come esempio.
- Dato y=vx, ne deriva dy/dx = x(dv/dx) + v.
- Da M dx + N dy = 0, abbiamo dy/dx = -M/N = f(v), poiché y è una funzione di v.
- Da cui f(v) = dy/dx = x(dv/dx) + v. Ora le variabili x e v possono essere separate: dx/x = dv/(f(v)-v)).
- Risolvi la nuova equazione differenziale con variabili separabili e quindi usa la sostituzione y=vx per trovare y.
-
3Se l’equazione differenziale non può essere risolta usando i due metodi spiegati qui sopra, prova a esprimerla come un’equazione lineare, nella forma dy/dx + Py = Q, dove P e Q sono funzioni della sola x o sono costanti. Nota che qui x e y possono essere usate indifferentemente. Se è così, continua come segue. Si veda la Figura 4 come esempio.
- Sia dato y=uv, dove u e v sono funzioni di x.
- Calcola il differenziale per ottenere dy/dx = u(dv/dx) + v(du/dx).
- Sostituisci in dy/dx + Py = Q, per ottenere u(dv/dx) + v(du/dx) + Puv = Q, o u(dv/dx) + (du/dx + Pu)v = Q.
- Determina u integrando du/dx + Pu = 0, dove le variabili sono separabili. Quindi usa il valore di u per trovare v risolvendo u(dv/dx) = Q, dove, di nuovo, le variabili sono separabili.
- Per finire, usa la sostituzione y=uv per trovare y.
-
4Risolvi l’equazione di Bernoulli</ref>: dy/dx + p(x) y = q(x) yn, come segue:
- Sia u = y1-n, in modo che du/dx = (1-n) y-n (dy/dx).
- Ne deriva che, y = u1/(1-n), dy/dx = (du/dx) yn / (1-n), e yn = un/(1-n).
- Sostituisci nell’equazione di Bernoulli e moltiplica per (1-n) / u1/(1-n), a dare
du/dx + (1-n) p(x) u = (1-n) q(x). - Nota che ora abbiamo un’equazione lineare di primo ordine con la nuova variabile u che può essere risolta con i metodi spiegati sopra (Passaggio 3). Una volta risolta, sostituisci y = u1/(1-n) per ottenere la soluzione completa.
Pubblicità
Risoluzione di Equazioni Differenziali di 2° Ordine
-
1Verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 5, dove f(y) è una funzione della sola y, o una costante. Se è così, segui i passaggi descritti in Figura 5.
-
2Risoluzione di equazioni differenziali lineari di secondo ordine con coefficienti costanti: Verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 6. Se è così, l’equazione differenziale può essere risolta semplicemente come un’equazione quadratica come mostrato nei passaggi successivi:
-
3Per risolvere un'equazione differenziale lineare di secondo ordine più generale, verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 7. Se questo è il caso, l’equazione differenziale può essere risolta seguendo i seguenti passaggi. Per un esempio, si vedano i passaggi in Figura 7.
- Risolvi l’equazione (1) della Figura 6 (dove f(x)=0) usando il metodo descritto sopra. Sia y = u la soluzione completa, dove u è la funzione complementare per l'equazione (1) in Figura 7.
- Per tentativi trova una soluzione particolare y = v dell'equazione (1) in Figura 7. Segui i passaggi seguenti:
- Se f(x) non è una soluzione particolare di (1):
- Se f(x) è nella forma f(x) = a + bx, assumi che y = v = A + Bx;
- Se f(x) è nella forma f(x) = aebx, assumi che y = v = Aebx;
- Se f(x) è nella forma f(x) = a1 cos bx + a2 sin bx, assumi che y = v = A1 cos bx + A2 sin bx.
- Se f(x) è una soluzione particolare di (1), assumi per v la forma sopra moltiplicata per x.
- Se f(x) non è una soluzione particolare di (1):
Pubblicità
La soluzione completa di (1) è data da y = u + v.
Risoluzione di Equazioni Differenziali di Ordine superiore
Le equazioni differenziali di ordine superiore sono molto più difficili da risolvere, ad eccezione di alcuni casi speciali:
-
1Verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 5, dove f(x) è una funzione della sola x, o una costante. Se è così, segui i passaggi descritti in Figura 8.
-
2Risoluzione di equazioni differenziali lineari dell'n-esimo ordine con coefficienti costanti: Verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 9. Se è così, l’equazione differenziale può essere risolta come segue:
-
3Per risolvere un'equazione differenziale lineare dell'n-esimo ordine più generale, verifica se l’equazione differenziale soddisfa la forma mostrata nell’equazione (1) in Figura 10. Se è questo il caso, l’equazione differenziale può essere risolta con un metodo simile a quello usato per risolvere equazioni differenziali lineari di secondo ordine, nel modo seguente:Pubblicità
Applicazioni Pratiche
-
Legge dell'interesse composto: la velocità dell'accumulo d’interesse è proporzionale al capitale iniziale. Più in generale, la velocità di cambiamento rispetto a una variabile indipendente è proporzionale al valore corrispondente della funzione. Cioè, se y = f(t), dy/dt = ky. Risolvendo con il metodo della variabile separabile, avremo y = ce^(kt), dove y è il capitale che si accumula all'interesse composto, c è una costante arbitraria, k è il tasso d'interesse (per esempio, l'interesse in dollari a un dollaro l’anno), t è il tempo. Ne deriva che il tempo è denaro.
- Nota che la legge dell’interesse composto si applica in molte aree della vita quotidiana. Per esempio, supponiamo di voler diluire una soluzione salina aggiungendo dell'acqua per ridurne la concentrazione salina. Quanta acqua dovrai aggiungere e come varia la concentrazione della soluzione rispetto alla velocità con cui fai scorrere l'acqua?
Sia s = quantità di sale nella soluzione in ogni momento, x = la quantità di acqua passata nella soluzione e v = il volume della soluzione. La concentrazione del sale nella miscela è data da s/v. Ora, supponiamo che un volume Δx fuoriesca dalla soluzione, cosi che la quantità di sale fuoriuscito sia (s/v)Δx, da cui il cambiamento nella quantità di sale, Δs, è dato da Δs = -(s/v)Δx. Dividi entrambi i lati per Δx, a dare Δs/Δx = -(s/v). Prendi il limite come Δx-->0, e avrai ds/dx = -s/v, che è un’equazione differenziale nella forma della legge dell’interesse composto, dove qui y è s, t è x e k è -1/v. -
La legge del raffreddamento di Newton’’’ è un'altra variante della legge dell’interesse composto. Afferma che la velocità di raffreddamento di un corpo rispetto alla temperatura dell'ambiente circostante è proporzionale alla differenza tra la temperatura del corpo e quella dell’ambiente circostante. Sia x = temperatura del corpo in eccesso rispetto all'ambiente circostante, t = tempo; avremo dx/dt = kx, dove k è una costante. La soluzione per questa equazione differenziale è x = ce^(kt), dove c è una costante arbitraria, come sopra. Supponiamo che la temperatura in eccesso, x, fosse dapprima pari a 80 gradi e che scenda a 70 gradi dopo un minuto. Come sarà dopo 2 minuti?
Dati t = tempo, x = temperatura in gradi, avremo 80 = ce^(k*0) = c. Inoltre, 70 = ce^(k*1) = 80e^k, così k = ln(7/8). Ne deriva che x = 70e^(ln(7/8)t) è una soluzione particolare di questo problema. Ora inserisci t = 2, avrai x = 70e^(ln(7/8)*2) = 53.59 gradi dopo 2 minuti. - In termodinamica, la pressione atmosferica p sopra il livello del mare cambia in proporzione all'altitudine h sopra il livello del mare. Anche qui si tratta di una variazione della legge dell'interesse composto. L’equazione differenziale in questo caso è dp/dh = kh, dove k è una costante.
- In chimica, la velocità di una reazione chimica, in cui x è la quantità trasformata in un periodo t, è il tasso temporale del cambiamento di x. Dato a = la concentrazione all'inizio della reazione, allora dx/dt = k(a-x), dove k è la costante della velocità. Anche questa è una variazione della legge d'interesse composto dove (a-x) è ora una variabile dipendente. Sia d(a-x)/dt = -k(a-x), so d(a-x)/(a-x) = -kdt. Integra, a dare ln(a-x) = -kt + a, dato che a-x = a quando t = 0. Riarrangiando, troviamo che la costante della velocità k = (1/t)ln(a/(a-x)).
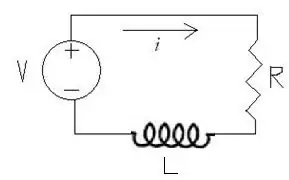
- Nell'elettromagnetismo, dato un circuito elettrico con una tensione V e una corrente i (ampere), la tensione V subisce una riduzione quando supera la resistenza R (ohm) del circuito e l'induzione L, secondo l’equazione V=iR + L(di/dt), oppure di/dt = (V - iR)/L. Anche questa è una variazione della legge d'interesse composto dove V - iR è ora la variabile dipendente.
- Nota che la legge dell’interesse composto si applica in molte aree della vita quotidiana. Per esempio, supponiamo di voler diluire una soluzione salina aggiungendo dell'acqua per ridurne la concentrazione salina. Quanta acqua dovrai aggiungere e come varia la concentrazione della soluzione rispetto alla velocità con cui fai scorrere l'acqua?
-
In acustica, una vibrazione armonica semplice ha un'accelerazione che è direttamente proporzionale al valore negativo della distanza. Ricordando che l'accelerazione è la derivata seconda della distanza, allora d2s/dt2 + k2s = 0, dove s = distanza, t = tempo, and k2 è la misura dell'accelerazione alla distanza unitaria. Si tratta della equazione di armonica semplice, un’equazione differenziale lineare di secondo ordine con coefficienti costanti, come risolto in Figura 6, equazioni (9) e (10). La soluzione è s = c1cos kt + c2sin kt.
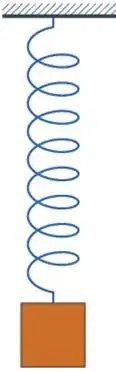
Si può ulteriormente semplificare stabilendo c1 = b sin A, c2 = b cos A. Sostituitele per ottenere b sin A cos kt + b cos A sin kt. Dalla trigonometria sappiamo che sin (x+y) = sin x cos y + cos x sin y, così che l’espressione si riduce a s = b sin (kt + A). L'onda che segue l’equazione armonica semplice oscilla tra b e -b con un periodo 2π/k.- Molla: prendiamo un oggetto di massa m collegato a una molla. Secondo la legge di Hooke, quando la molla si allunga o si comprime di s unità rispetto alla sua lunghezza iniziale (anche detta posizione d'equilibrio), esercita una forza di ripristino F proporzionale a s, ovvero F = -k2s. In base alla seconda legge di Newton (la forza è uguale al prodotto della massa per l'accelerazione), avremo m d2s/dt2 = -k2s, o m d2s/dt2 + k2s = 0, che è un'espressione dell’equazione armonica semplice.
-
Vibrazioni smorzate: considera la molla in vibrazione come sopra, con una forza smorzante. Qualsiasi effetto, come la forza di attrito, che tende a ridurre l’ampiezza delle oscillazioni in un oscillatore, viene definito una forza smorzante. Per esempio, una forza smorzante è fornita da un armotizzatore di un'auto. In genere, la forza smorzante, Fd, è approssimativamente proporzionale alla velocità dell'oggetto, ovvero Fd = -c2 ds/dt, dove c2 è una costante. Combinando la forza smorzante con la forza di ripristino, avremo -k2s - c2 ds/dt = m d2s/dt2, in base alla seconda legge di Newton. Oppure, m d2s/dt2 + c2 ds/dt + k2s = 0. Questa equazione differenziale è un’equazione lineare di secondo ordine che può essere risolta risolvendo l’equazione ausiliaria mr2 + c2r + k2 = 0, dopo aver sostituito s = e^(rt).
Risolvi con la formula quadratica r1 = (-c2 + sqrt(c4 - 4mk2)) / 2m; r2 = (-c2 - sqrt(c4 - 4mk2)) / 2m.- Sovrasmorzamento: Se c4 - 4mk2 > 0, r1 e r2 sono reali e distinti. La soluzione è s = c1e^(r1t) + c2e^(r2t). Dato che c2, m, and k2 sono positivi, sqrt(c4 - 4mk2) deve essere minore di c2, il che implica che entrambe le radici, r1 e r2, sono negative, e la funzione è in decadimento esponenziale. In questo caso, non avviene un'oscillazione. Una forte forza smorzante, per esempio, può essere data da un olio a elevata viscosità o da un lubrificante.
- Smorzamento critico: Se c4 - 4mk2 = 0, r1 = r2 = -c2 / 2m. La soluzione è s = (c1 + c2t)e^((-c2/2m)t). Anche questa è un decadimento esponenziale, senza oscillazione. La minima diminuzione, tuttavia, nella forza smorzante causerà l'oscillazione dell’oggetto una volta superato il punto di equilibrio.
- Sottosmorzamento: Se c4 - 4mk2 < 0, le radici sono complesse, date da -c/2m +/- ωi, dove ω = sqrt(4mk2 - c4)) / 2m. La soluzione è s = e^(-(c2/2m)t) (c1 cos ωt + c2 sin ωt). Si tratta di un'oscillazione smorzata dal fattore e^(-(c2/2m)t. Dato che c2 e m sono entrambe positive, e^(-(c2/2m)t) tenderà a zero quando t si avvicina all'infinito. Ne deriva che prima o poi il moto decadrà a zero.
Consigli
- Sostituisci la soluzione nell’equazione differenziale originale per vedere che l’equazione sia soddisfatta. In questo modo puoi verificare se la soluzione è corretta.
- Nota: l'inverso del calcolo differenziale è detto calcolo integrale, che si occupa della somma degli effetti di quantità che cambiano continuamente; per esempio, il calcolo della distanza (confronta con d = rt) coperta da un oggetto le cui variazioni istantanee (velocità) in un intervallo tempo sono note.
- Molte equazioni differenziali non sono risolvibili con i metodi descritti sopra. I metodi sopra, tuttavia, sono sufficienti per risolvere molte equazioni differenziali comuni .
Avvertenze
- A differenza del calcolo differenziale, in cui è possibile calcolare la derivata di una data espressione, il calcolo integrale di molte espressioni non può essere calcolato. Per cui non perdere tempo nel tentativo di integrare un'espressione che non può essere integrata. Controlla in una tabella degli integrali per essere sicuro. La soluzione di un’equazione differenziale è considerata significativa quando è stata ridotta a un'espressione contenente integrali, non importa se l'integrazione è possibile o no.
Cose che ti Serviranno
- Dei fogli
- Penna o matita
- Una tabella degli integrali potrebbe essere d'aiuto





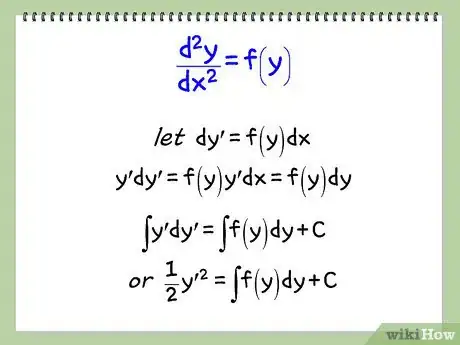


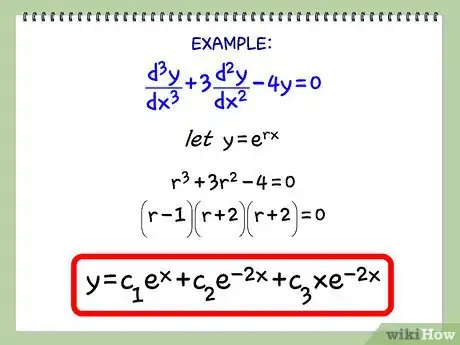







-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
