Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 15 045 volte
I fattoriali vengono spesso usati per il calcolo delle probabilità e delle permutazioni o per i possibili ordini degli eventi.[1] Il fattoriale di un numero è indicato dal segno e prevede di moltiplicare tutti gli interi discendenti a partire da quel numero. Una volta che hai capito cos'è un fattoriale, è molto semplice calcolarlo, specialmente con l'aiuto di una calcolatrice scientifica.
Passaggi
Calcolare un Fattoriale
-
1Determina il numero di cui devi calcolare il fattoriale. Un fattoriale è indicato con un intero positivo e un punto esclamativo.
- Per esempio, se devi calcolare il fattoriale di 5, vedrai .
-
2Scrivi la sequenza dei numeri da moltiplicare. Un fattoriale di un numero è semplicemente il prodotto degli interi positivi in ordine discendente rispetto a quel numero, fino a 1.[2] In termini di formule, , in cui è un intero positivo.[3]
- Per esempio, se stai calcolando , avresti oppure, più semplicemente: .
-
3Moltiplica i numeri. Puoi calcolare velocemente un fattoriale con una calcolatrice scientifica, che dovrebbe avere il simbolo . Se invece vuoi fare il calcolo a mano, per semplificarlo cerca prima due fattori che moltiplicati danno 10.[4] Naturalmente, puoi ignorare anche l'1, perché tutti i numeri moltiplicati per 1 non cambiano.
- Per esempio, se devi calcolare , ignora l'1, poi inizia da . Ora ti restano solo . Dato che , sai che .
Pubblicità
Semplificare un Fattoriale
-
1Determina l'espressione da semplificare. Spesso comparirà come frazione.
- Per esempio, potresti dover semplificare .
-
2Scrivi i fattori di ciascun fattoriale. Dato che il fattoriale è un fattore di tutti i fattoriali di interi più grandi, per semplificare devi cercare fattori che puoi cancellare.[5] Se scrivi tutti i termini, diventa più facile.
- Per esempio, se vuoi semplificare , riscrivi l'espressione come
-
3Annulla tutti i termini comuni al numeratore e al denominatore.[6] In questo modo semplificherai i numeri rimasti da moltiplicare.
- Per esempio, dato che è un fattore di , puoi cancellare dal numeratore e dal denominatore:
- Per esempio, dato che è un fattore di , puoi cancellare dal numeratore e dal denominatore:
-
4Completa i calcoli. Semplifica, se possibile. In questo modo otterrai l'espressione finale semplificata.
- Per esempio:
Quindi, semplificato è .
Pubblicità - Per esempio:
Risolvere Problemi Fattoriali Semplici
-
1Considera l'espressione 8!.
- Se stai usando una calcolatrice scientifica, premi il tasto , poi il tasto .
- Se esegui il calcolo a mano, scrivi i fattori da moltiplicare:
- Ignora l'1:
- Porta fuori :
- Raggruppa per primi tutti i numeri facili da moltiplicare, poi svolgi i prodotti:
Quindi, .
-
2Semplifica l'espressione: .
- Scrivi i fattori di ciascun fattoriale:
- Annulla i termini comuni a numeratore e denominatore:
- Completa i calcoli:
Quindi, l'espressione si semplifica con .
- Scrivi i fattori di ciascun fattoriale:
-
3Prova il problema seguente. Immagina di avere 6 quadri che vuoi mettere in mostra su un muro. In quanti modi puoi ordinarli?
- Dato che stai cercando di calcolare in quanti modi è possibile ordinare gli oggetti, puoi risolvere il problema semplicemente calcolando il fattoriale del numero di oggetti.
- Puoi calcolare il numero delle possibili disposizioni per 6 quadri appesi in fila risolvendo .
- Se stai usando una calcolatrice scientifica, premi il tasto , seguito dal tasto .
- Se esegui il calcolo a mano, scrivi i fattori da moltiplicare:
- Ignora l'1:
- Porta fuori :
- Raggruppa per primi gli altri numeri facili da moltiplicare, poi esegui tutti i prodotti:
Quindi, 6 quadri appesi in fila possono essere ordinati in 720 modi diversi.
-
4Prova il problema seguente. Hai 6 quadri. Immagina di disporne 3 in una fila su una parete. In quanti modi puoi ordinare 3 quadri?
- Dato che hai 6 quadri diversi, ma ne usi solo 3, devi moltiplicare solo i primi 3 numeri nella sequenza del fattoriale di 6. Puoi usare la formula , in cui è uguale al numero di oggetti che stai usando. Questa formula funziona solo se non ci sono ripetizioni (un oggetto non può essere scelto più di una volta) e se l'ordine ha importanza (vuoi scoprire i vari modi in cui gli elementi possono essere ordinati).[7]
- Puoi calcolare il numero di disposizioni possibili per 3 quadri scelti tra 6 e disposti in fila risolvendo .
- Sottrai i numeri nel denominatore:
- Scrivi i fattori di ciascun fattoriale:
- Annulla i termini comuni di numeratore e denominatore:
- Completa i calcoli: .
Quindi 3 quadri scelti tra 6 possono essere ordinati in 120 modi diversi, se appesi in fila.
Pubblicità
Consigli
- 1! = 1 per definizione.
- Anche se non è intuitivo, puoi assumere 0! = 1 quando non viene indicato altrimenti.
- I fattoriali vengono usati per risolvere i problemi combinatori, quindi esercitati in questa capacità.
- Ricorda di controllare sempre il tuo lavoro.
Riferimenti
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html
- ↑ https://www.mathsisfun.com/numbers/factorial.html
- ↑ http://mathworld.wolfram.com/Factorial.html
- ↑ http://www.themathpage.com/aprecalc/factorial.htm
- ↑ http://www.themathpage.com/aprecalc/factorial.htm
- ↑ http://www.purplemath.com/modules/factorial.htm
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html



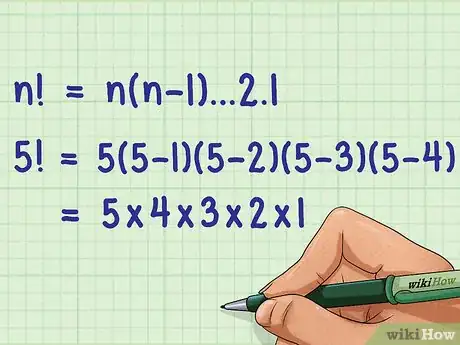




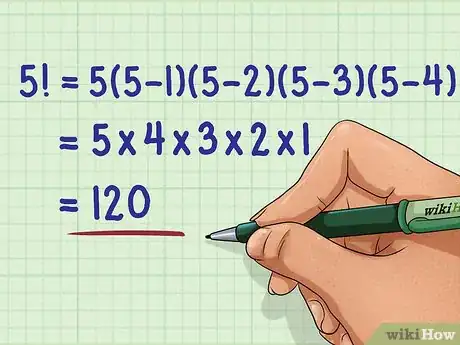






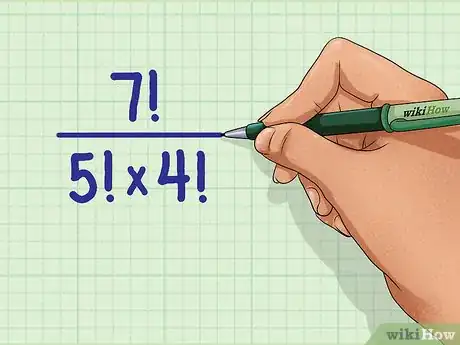







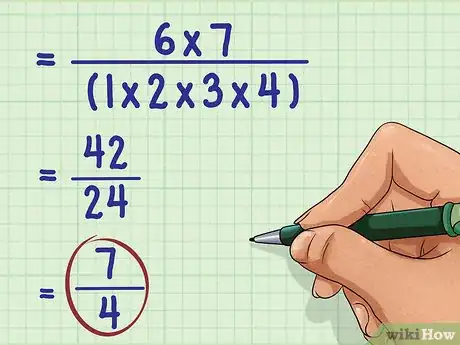
























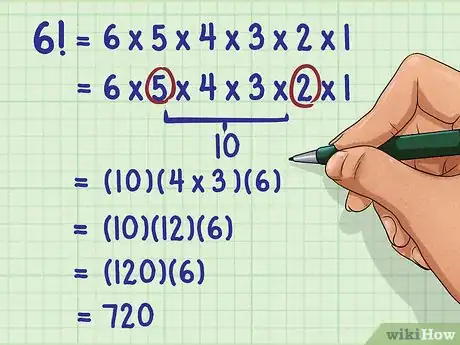




















-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 15 045 volte