X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 18 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 72 827 volte
Confuso dai logaritmi? Non preoccuparti! Un logaritmo (abbreviato log) non è altro che un esponente in una forma diversa.
logax = y è la stessa cosa di ay = x.
Passaggi
-
1Conosci la differenza tra equazioni logaritmiche ed esponenziali. È un passaggio molto semplice. Se contiene un logaritmo (ad esempio: logax = y) è un problema logaritmico. Un logaritmo è rappresentato dalle lettere "log".Se l'equazione contiene un esponente (che è una variabile elevata a una potenza), allora è un'equazione esponenziale. Un esponente è un numero scritto all'apice dopo un altro numero.
- Logaritmica: logax = y
- Esponenziale: ay = x
-
2Impara le parti di un logaritmo. La base è il numero sottoscritto dopo le lettere "log" – 2 in questo esempio. L'argomento o il numero è il numero che segue il numero sottoscritto – 8 in questo esempio. Il risultato è il numero che l'espressione logaritmica pone uguale a – 3 in questa equazione.
-
3Conosci la differenza tra un logaritmo comune e un logaritmo naturale.
- log comune: sono in base 10 (ad esempio, log10x). Se un logaritmo è scritto senza la base (come log x), allora si assume che la base sia 10.
- log naturale: sono logaritmi in base e. e è una costante matematica che è uguale al limite di (1 + 1/n)n con n che tende a infinito, approssimativamente 2,718281828. (ha molte più cifre di quelle riportate qui) logex viene spesso scritto come ln x.
- Altri logaritmi: altri logaritmi hanno la base diversa da 10 ed e. Logaritmi binari sono in base 2 (per esempio, log2x). Logaritmi esadecimali sono in base 16 (per esempio log16x o log#0fx in notazione esadecimale). Logaritmi in base 64th sono molto complessi, e solitamente ristretti a calcoli di geometria molto avanzata.
-
4Conosci e applica le proprietà dei logaritmi. Le proprietà dei logaritmi ti permettono di risolvere equazioni logaritmiche ed esponenziali altrimenti impossibili da risolvere. Funzionano solo se la base a e l'argomento sono positivi. Inoltre la base a non può essere 1 o 0. Le proprietà dei logaritmi sono elencate qui sotto con un esempio per ognuna di loro, con numeri al posto delle variabili. Queste proprietà sono utili per risolvere le equazioni.
- loga(xy) = logax + logay
Un logaritmo di due numeri, x e y, che vengono moltiplicati tra loro, può essere diviso in due log separati: un log di ognuno dei fattori aggiunti insieme (funziona anche all'inverso).
Esempio:
log216 =
log28*2 =
log28 + log22 - loga(x/y) = logax - logay
Un log di due numeri diviso per ognuno di loro, x e y, può essere diviso in due logaritmi: il log del dividendo x meno il log del divisore y.
esempio:
log2(5/3) =
log25 - log23 - loga(xr) = r*logax
Se l'argomento x del log ha un esponente r, l'esponente può essere spostato davanti al logaritmo.
Esempio:
log2(65)
5*log26 - loga(1/x) = -logax
Guarda l'argomento. (1/x) è uguale a x-1. Questa è un'altra versione della precedente proprietà.
Esempio:
log2(1/3) = -log23 - logaa = 1
Se la base a è uguale all'argomento a, il risultato è 1. Questo è molto facile da ricordare se si pensa al logaritmo in forma esponenziale. Quante volte si dovrebbe moltiplicare a per se stesso per avere a? Una sola volta.
Esempio:
log22 = 1 - loga1 = 0
Se l'argomento è 1, il risultato è sempre 0. Questa proprietà è vera perché qualunque numero con esponente 0 è uguale a 1.
Esempio:
log31 =0 - (logbx/logba) = logax
Questa è conosciuta come "cambio di base".[1] Un logaritmo diviso per un altro, entrambi con la stessa base b, è uguale al singolo logaritmo. L'argomento a del denominatore diventa la nuova base, e l'argomento x del numeratore diventa il nuovo argomento. È facile da ricordare se pensi alla base come alla base di un oggetto e il denominatore come la base di una frazione.
Esempio:
log25 = (log 5/log 2)
- loga(xy) = logax + logay
-
5Esercitati con le proprietà. Le proprietà vengono memorizzate esercitandosi a risolvere le equazioni. Ecco un esempio di equazione che può essere risolta con una delle proprietà:
4x*log2 = log8 dividi entrambi per log2.
4x = (log8/log2) Usa il cambio di base.
4x = log28 Computa il valore del log.4x = 3 Dividi entrambi per 4. x = 3/4 Fine.Pubblicità
Consigli
- "2,7jacksonjackson" è un trucco molto utile per memorizzare il valore di e: 1828 è l'anno in cui Andrew Jackson venne eletto Presidente degli Stati Uniti, quindi “jacksonjackson” sta per 18281828 (ricorda che il valore di e è 2,718281828).
Pubblicità
Riferimenti
Informazioni su questo wikiHow
Pubblicità
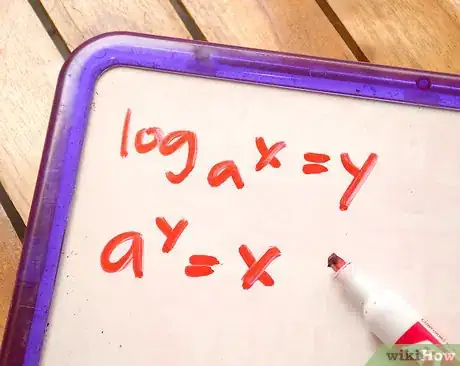
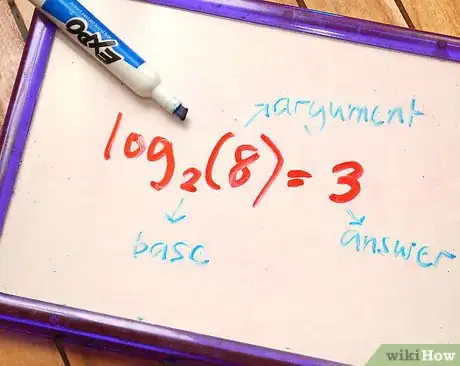
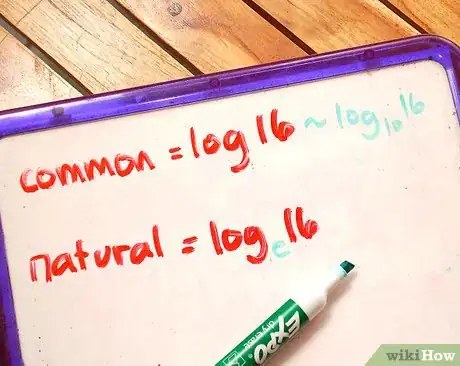
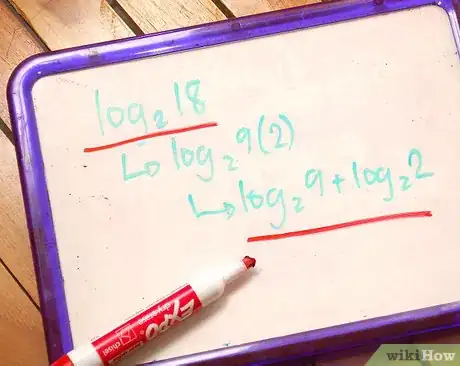
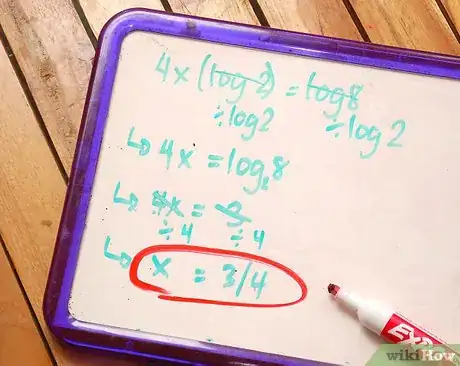




-to-Grams-(g)-Step-12-Version-4.webp)













