Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 9 067 volte
Un numero decimale periodico è un valore espresso in notazione decimale con una stringa finita di cifre che da un certo punto in poi si ripete all'infinito. Non è facile lavorare con questi numeri, ma possono essere convertiti in frazioni. A volte, le cifre decimali periodiche vengono contrassegnate con un trattino; per esempio, il numero 3,7777 con 7 periodico può anche essere riportato come 3,7. Per trasformare un numero come questo in una frazione, devi impostare un'equazione, svolgere delle moltiplicazioni e delle sottrazioni per rimuovere la cifra periodica e risolvere infine l'equazione stessa.
Passaggi
Convertire dei Numeri Decimali Periodici Elementari
-
1Individua le cifre periodiche. Per esempio, il numero 0,4444 ha come cifra periodica 4. Si tratta di un numero elementare, perché non esiste una porzione decimale non periodica. Conta quante cifre periodiche ci sono.
- Una volta scritta l'equazione, devi moltiplicarla per 10^y, dove y corrisponde al numero delle cifre presenti nella porzione periodica.[1]
- Nell'esempio di 0,4444, c'è una sola cifra ripetuta, puoi quindi moltiplicare l'equazione per 10^1.
- Se prendi in considerazione il numero 0,4545, la porzione periodica è composta da due cifre; di conseguenza, moltiplichi l'equazione per 10^2.
- Se ci fossero tre cifre, il fattore sarebbe 10^3 e così via.
-
2Riscrivi il numero decimale sotto forma di equazione. Esprimila in modo che "x" sia pari al numero originale.[2] Nell'esempio considerato, l'equazione è x = 0,4444; dato che c'è una sola cifra periodica, moltiplica il tutto per 10^1 (che corrisponde a 10).[3]
- Nell'esempio: x = 0,4444, quindi 10x = 4,4444.
- Se consideri x = 0,4545 in cui ci sono due cifre periodiche, devi moltiplicare entrambi i termini per 10^2 (cioè 100) ottenendo 100x = 45,4545.
-
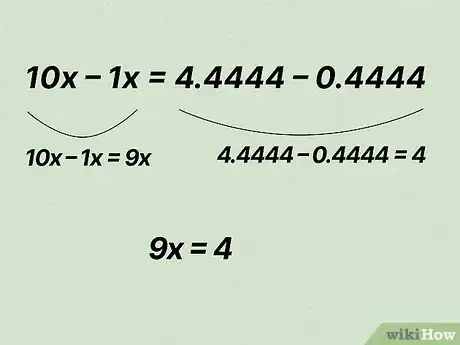
3Rimuovi la porzione periodica. Puoi farlo sottraendo x da 10x. Ricorda che ogni operazione eseguita sul termine destro dell'equazione deve essere riportata anche su quello sinistro:[4]
- 10x – 1x = 4,4444 – 0,4444;
- Sul lato sinistro ottieni 10x - 1x = 9x; su quello destro 4,4444 – 0,4444 = 4;
- Di conseguenza: 9x = 4.
-
4Risolvi per x. Quando sai a che cosa corrisponde 9x, puoi trovare il valore di x dividendo entrambi i termini dell'equazione per 9:
- Sul lato destro hai 9x ÷ 9 = x, mentre sul sinistro ottieni 4/9;
- Puoi quindi affermare che x = 4/9 e che quindi il numero decimale periodico 0,4444 può essere riscritto sotto forma di frazione 4/9.
-
5Riduci la frazione. Semplificala ai minimi termini (se possibile), dividendo sia il numeratore sia il denominatore per il massimo comune divisore.[5]
- Nell'esempio descritto in precedenza, 4/9 è già ai minimi termini.
Pubblicità
Convertire Numeri con Decimali Periodici e Non Periodici
-
1Determina le cifre periodiche. Non è insolito trovare un numero con una porzione non periodica prima della sequenza che si ripete, ma anche in questo caso puoi procedere alla conversione in frazione.
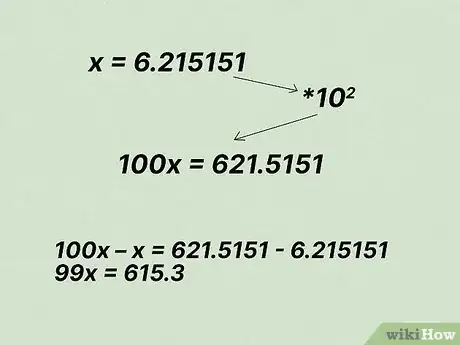
- Per esempio, prendi in esame il numero 6,215151; in questo caso, 6,2 non è periodico mentre 15 lo è.
- Anche questa volta devi annotare di quante cifre è composta la porzione che si ripete, perché devi moltiplicare per 10^y, dove "y" è proprio la quantità di tali cifre.
- In questo esempio ci sono due cifre che si ripetono, devi quindi moltiplicare l'equazione per 10^2.
-
2Scrivi il problema sotto forma di equazione, poi sottrai la parte periodica. Anche in tal caso, se x = 6,215151, ne consegue che 100x = 621,5151. Per rimuovere le cifre che si ripetono, sottrai da entrambi i termini dell'equazione:
- 100x – x (= 99x) = 621,5151 – 6,215151 (= 615,3);
- Quindi 99x = 615,3.
-
3Risolvi per x. Dato che 99x = 615,3 dividi entrambi i termini per 99; così facendo, ricavi x = 615,3/99.
-
4Rimuovi la cifra decimale al numeratore. Per farlo, ti basta moltiplicare sia il numeratore sia il denominatore per 10^z, dove z corrisponde al numero di cifre decimali che devi eliminare. In 615,3 devi spostare la virgola di un solo posto, il che significa che devi moltiplicare per 10^1:
- 615,3 x 10 / 99 x 10 = 6153/990;
- Semplifica la frazione dividendo il numeratore e il denominatore per il massimo comune divisore, che in questo caso è 3: x = 2051/330.
Pubblicità
Riferimenti
- ↑ http://www.virtualnerd.com/tutorials/?id=PreAlg_05_01_0037
- ↑ http://www.basic-mathematics.com/converting-repeating-decimals-to-fractions.html
- ↑ https://www.khanacademy.org/math/algebra/alg-1-old-content/conv_rep_decimals/v/coverting-repeating-decimals-to-fractions-1
- ↑ http://www.virtualnerd.com/tutorials/?id=PreAlg_05_01_0037
- ↑ https://www.khanacademy.org/math/algebra/alg-1-old-content/conv_rep_decimals/v/coverting-repeating-decimals-to-fractions-2


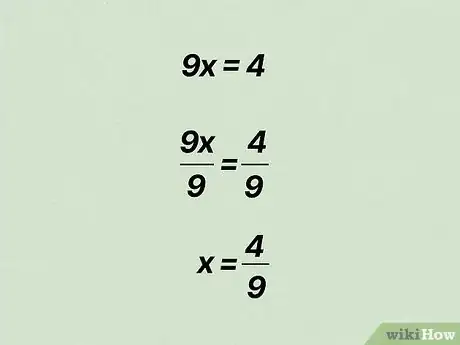







-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 9 067 volte