Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 43 374 volte
Se hai studiato analisi matematica, hai sicuramente imparato la regola della potenza per trovare la derivata delle funzioni di base. Tuttavia, quando la funzione contiene una radice quadrata o un simbolo radicale, come , sembra difficile poter applicare tale norma. Attraverso una semplice sostituzione degli esponenti, l'operazione diventa invece molto semplice; puoi usare il medesimo metodo e sfruttare la regola della catena per differenziare molte altre funzioni che includono dei radicali.
Passaggi
Usare la Regola della Potenza
-
1Ripassa la regola della potenza delle derivate. Si tratta probabilmente del primo metodo che hai appreso per trovare le funzioni derivate e che afferma che per una variabile elevata a qualsiasi potenza , la derivata è:[1]
- ;
- ;
- Per esempio, rileggi le seguenti funzioni e le relative derivate:
- Se , allora ;
- Se , allora ;
- Se , allora ;
- Se , allora .
-
2Riscrivi la radice quadrata come una potenza. Per trovare la derivata di una funzione radicale devi ricordare che la radice quadrata di un numero o di una variabile può essere riscritta sotto forma di potenza. Il termine che si trova sotto il segno di radice (radicando) viene riproposto come base della potenza e il suo esponente è il reciproco dell'indice; nel caso di radice quadrata questo corrisponde a ½. Considera gli esempi che seguono:[2]
- ;
- ;
- .
-
3Applica la regola della potenza. Se la funzione è una semplice radice quadrata, , sfrutta questo metodo come descritto di seguito per trovare la relativa derivata:[3]
- (scrivi la funzione originale);
-
(riscrivi il radicale come una potenza);
- (trova la derivata con la regola della potenza);
- (semplifica la potenza).
-
4Semplifica il risultato. In questa fase devi sapere che una potenza con esponente negativo corrisponde al reciproco della base elevata al medesimo esponente, ma con segno positivo. Di conseguenza, l'esponente indica che hai la radice quadrata della base al denominatore di una frazione.[4]
- Continuando con l'esempio precedente, la derivata può essere semplificata come segue:
- ;
- ;
- .
Pubblicità - Continuando con l'esempio precedente, la derivata può essere semplificata come segue:
Usare la Regola della Catena
-
1Ripassa la regola della catena per le funzioni. Si tratta di un metodo per le derivate che viene utilizzato quando la funzione originale combina due funzioni. Questa regola afferma che per due funzioni e la derivata della combinazione delle due può essere trovata come segue:[5]
- Se , allora .
-
2Definisci le funzioni per la regola della catena. Per applicare tale norma devi prima definire le due funzioni che costituiscono quella combinata. Quando si tratta di funzioni radicali, quella esterna, , è quella radicale e quella interna, , è il radicando.[6]
- Per esempio, supponi di voler trovare la derivata di . Definisci le due funzioni in questo modo:
- ;
- .
- Per esempio, supponi di voler trovare la derivata di . Definisci le due funzioni in questo modo:
-
3Trova le derivate delle due funzioni. Per applicare la regola della catena a questo genere di funzioni devi prima trovare la derivata della funzione radicale generale:[7]
-
;
- ;
- .
- In seguito calcola la derivata della seconda funzione:
- ;
- .
-
;
-
4Combina quanto trovato con la regola della catena. Per prima cosa ripassa la norma: ; in seguito, combina le derivate come segue:[8]
- ;
- ;
- .
Pubblicità
Usare una Scorciatoia per le Derivate delle Funzioni Radicali
-
1Impara la scorciatoia per calcolare le derivate di qualsiasi funzione radicale. Ogni volta che devi trovare la derivata della radice quadrata di una variabile o di una funzione, puoi applicare un semplice schema. La derivata sarà sempre la derivata del radicando diviso il doppio della radice quadrata originale. In linguaggio matematico questa regola si esprime come:[9]
- Se , allora .
-
2Trova la derivata del radicando. Si tratta del termine o della funzione che si trova sotto il simbolo di radice; per applicare questo metodo rapido devi trovare la derivata di tale elemento. Osserva gli esempi seguenti:[10]
- Nella funzione il radicando è e la sua derivata è ;
- Nella funzione il radicando è e la sua derivata ;
- Nella funzione il radicando è e la sua derivata .
-
3Scrivi la derivata del radicando come numeratore di una frazione. Quando si calcola la derivata di una funzione radicale, si procede con una frazione il cui numeratore è la derivata del radicando. Di conseguenza, considerando le funzioni semplici prese in esame ottieni:[11]
- Se , allora ;
- Se , allora ;
- Se , allora .
-
4Scrivi il denominatore come il doppio della radice quadrata originale. Usando questa scorciatoia il denominatore è pari a due volte la funzione radicale originale; considerando gli esempi precedenti ottieni:[12]
- Se , allora ;
- Se , allora ;
- Se , allora .
-
5Unisci il numeratore e il denominatore per trovare la derivata. Combina le due metà della frazione, il risultato è la derivata della funzione originale.[13]
- Se , allora ;
- Se , allora ;
- Se , allora .
Pubblicità
Riferimenti
- ↑ https://www.mathsisfun.com/calculus/derivatives-rules.html
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U16_L1_T3_text_final.html
- ↑ https://www.mathsisfun.com/calculus/derivatives-rules.html
- ↑ http://www.mathsisfun.com/algebra/negative-exponents.html
- ↑ https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/chainruledirectory/ChainRule.html
- ↑ https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/chainruledirectory/ChainRule.html
- ↑ https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/chainruledirectory/ChainRule.html
- ↑ https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/chainruledirectory/ChainRule.html
- ↑ http://www.ditutor.com/derivatives/derivative_square.html

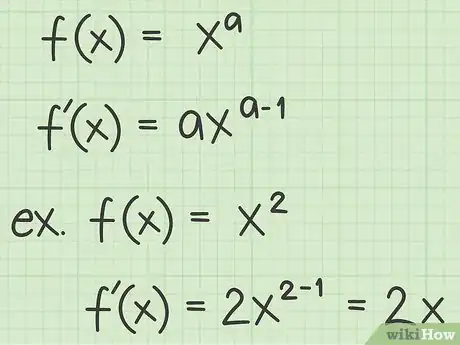












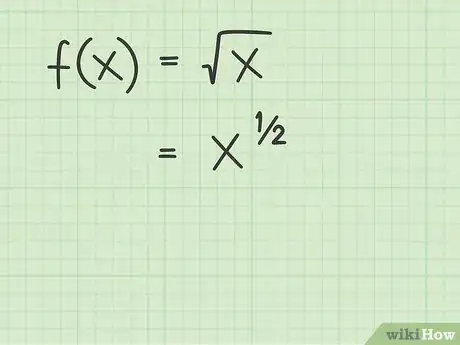



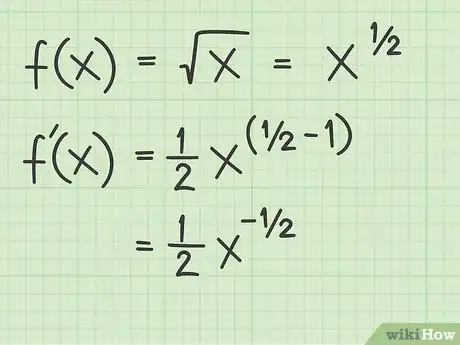





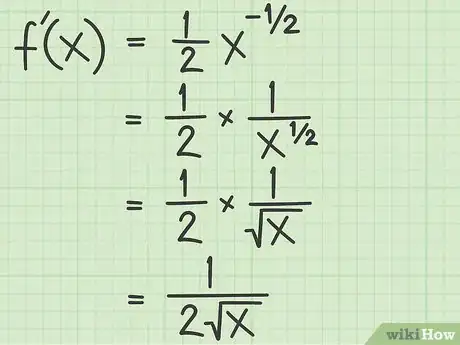




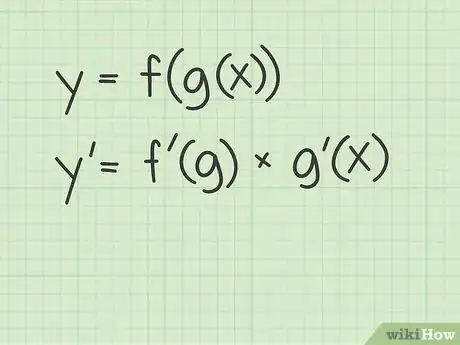




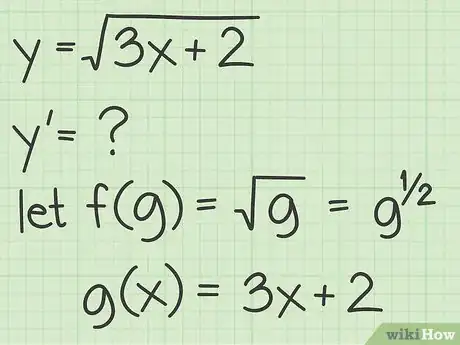




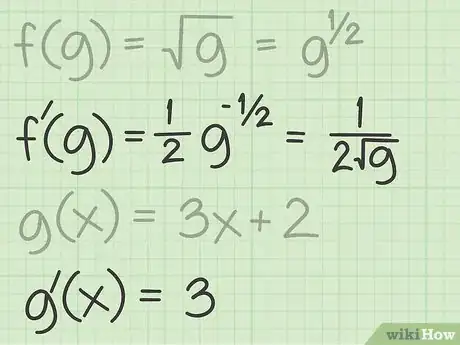



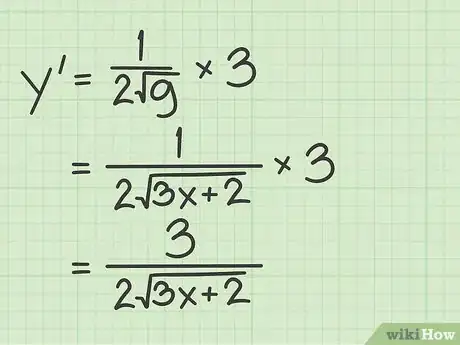



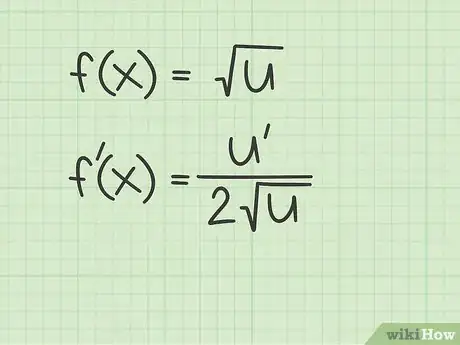


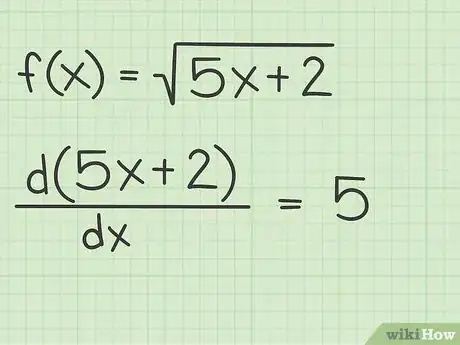









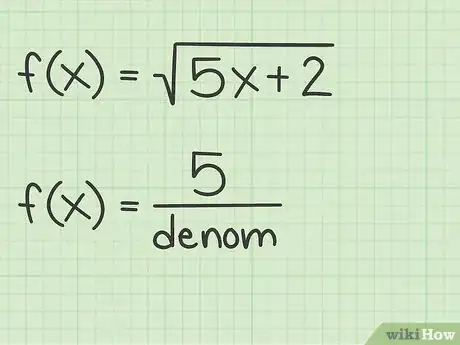






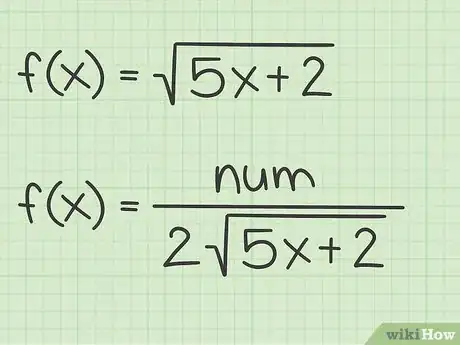



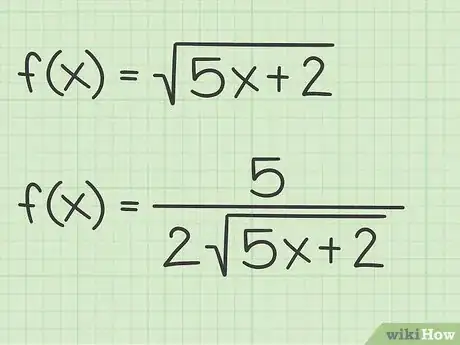







-to-Grams-(g)-Step-12-Version-4.webp)














Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 43 374 volte