Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 63 357 volte
Un criterio per classificare le funzioni è determinare se sono "pari", "dispari" o se non rientrano in nessuna delle due categorie; questi termini fanno riferimento alla ciclicità o alla simmetria della funzione stessa. Il modo migliore per giungere a questa conclusione è manipolarla algebricamente, ma è anche possibile visualizzare il grafico per osservarne la simmetria. Una volta imparato a classificare le funzioni, puoi prevedere l'aspetto di determinate combinazioni.
Passaggi
per Via Algebrica
-
1Ripassa le variabili opposte. In algebra, l'opposto di una variabile viene scritto con un segno negativo; questo concetto si applica indipendentemente dal fatto che la funzione contenga una o qualsiasi altra variabile. Se questa è già negativa (o è presente una sottrazione), il suo opposto è una variabile positiva (o addizione). Ecco alcuni esempi di variabili e dei rispettivi opposti:[1]
- L'opposto di è ;
- L'opposto di è ;
- L'opposto di è .
-
2Sostituisci ogni variabile presente nella funzione con il suo opposto. Altera la funzione originale solamente per quanto riguarda il segno delle variabili. Per esempio:[2]
- diventa ;
- diventa ;
- diventa .
-
3Semplifica la nuova funzione. In questa fase non devi preoccuparti di risolverla per un determinato valore; devi semplicemente semplificarla per confrontare la versione nuova, f(-x), con quella originale, f(x). Ricorda le regole elementari delle potenze, secondo cui una base negativa elevata a un esponente pari genera un numero positivo, mentre una base negativa elevata a un esponente dispari genera un numero negativo.[3]
-
;
- ;
-
;
- ;
- ;
-
;
- .
-
;
-
4Confronta le due funzioni. Per ogni esempio che stai considerando, confronta la versione semplificata di f(-x) con la rispettiva f(x); allinea i termini fra loro per facilitare il processo e valutane il segno.[4]
- Se le due versioni sono identiche, significa che f(x)=f(-x), di conseguenza la funzione originale è pari. Ad esempio:
- e .
- Le due funzioni sono identiche, quindi l'originale è pari.
- Se ogni termine della nuova versione della funzione è opposto al rispettivo termine della versione originale, significa che f(x)=-f(-x), di conseguenza la funzione è dispari. Per esempio:
- ma .
- Nota che se moltiplichi ciascun termine della prima funzione per -1, crei una nuova funzione. Questo significa che l'originale, g(x), è dispari.
- Se la nuova funzione non rientra in questi due esempi, puoi affermare che non è né pari né dispari. Ecco un esempio:
- ma . Il primo termine è invariato ma il secondo è l'opposto; di conseguenza la funzione non è pari e non è dispari.
Pubblicità - Se le due versioni sono identiche, significa che f(x)=f(-x), di conseguenza la funzione originale è pari. Ad esempio:
per Via Grafica
-
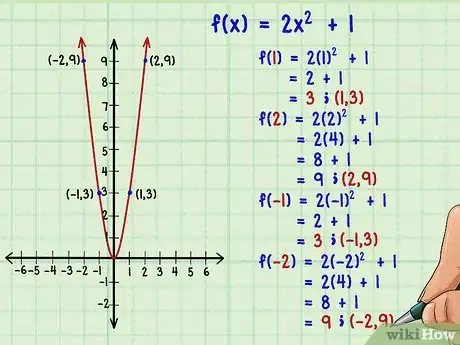
1Traccia il grafico della funzione. Usa della carta millimetrata o una calcolatrice scientifica; assegna diversi valori a , inseriscili nell'equazione e calcola i rispettivi di . Riporta le coppie sul grafico e, dopo aver individuato diversi punti, collegali per disegnare il grafico.[5]
- Quando determini i punti, controlla i valori positivi e quelli negativi corrispondenti di . Per esempio, se stai considerando la funzione , usa questi dati:
- ; di conseguenza le coordinate sono ;
- ; il punto grafico è definito dalla coppia ;
- ; il punto corrisponde a ;
- ; ottieni le coordinate .
- Quando determini i punti, controlla i valori positivi e quelli negativi corrispondenti di . Per esempio, se stai considerando la funzione , usa questi dati:
-
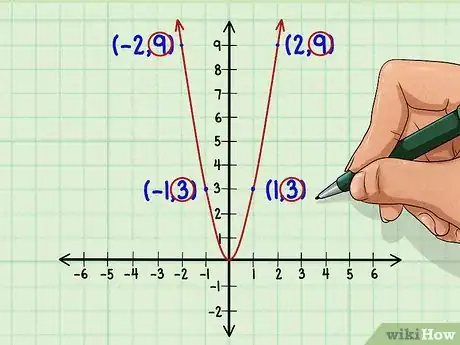
2Verifica la simmetria del grafico rispetto all'asse delle ordinate. Quando osservi la versione grafica di una funzione, puoi notare che una metà "rispecchia" l'altra; in altre parole è simmetrica. Se noti che la parte a destra dell'asse delle y (positiva) coincide con quella a sinistra (negativa), la funzione è pari.[6]
- Puoi testare la simmetria scegliendo singolarmente dei punti. Se il valore di y per un determinato valore di x è identico a quello generato da -x, la funzione è pari. I punti che sono stati selezionati in precedenza per tracciare il grafico di hanno portato ai seguenti risultati:
- (1,3) e (-1,3);
- (2,9) e (-2,9).
- I valori immutati di y per x=1, x=-1 e per x=2, x=-2 segnalano che la funzione è pari. Per una prova inconfutabile, due coppie di dati non sono sufficienti, ma rappresentano una buona indicazione di massima.
- Puoi testare la simmetria scegliendo singolarmente dei punti. Se il valore di y per un determinato valore di x è identico a quello generato da -x, la funzione è pari. I punti che sono stati selezionati in precedenza per tracciare il grafico di hanno portato ai seguenti risultati:
-
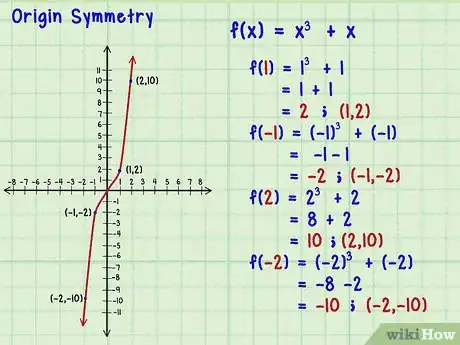
3Controlla la simmetria rispetto all'origine. Si tratta del punto centrale (0,0) in cui si intersecano gli assi del sistema. Quando si parla di simmetria rispetto all'origine significa che per ciascun valore positivo di x si ottiene un y positivo e che per ciascun valore -x si ottiene un y negativo e viceversa; le funzioni dispari sono simmetriche rispetto all'origine.[7]
- Se scegli una serie di dati per x e i relativi opposti (-x), dovresti ottenere risultati opposti di y. Considera la funzione . Questa genera la seguente serie di punti:
- ; il punto ha coordinate (1,2);
- ; la coppia di dati è (-1,-2);
- ; ottieni (2,10);
- ; il punto è definito da (-2,-10).
- Di conseguenza, puoi affermare che f(x)=-f(-x) e puoi concludere che sia dispari.
- Se scegli una serie di dati per x e i relativi opposti (-x), dovresti ottenere risultati opposti di y. Considera la funzione . Questa genera la seguente serie di punti:
-
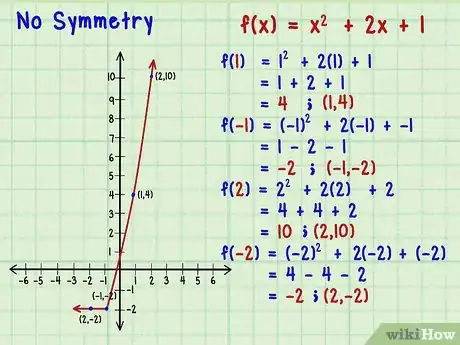
4Cerca l'assenza della simmetria. L'esempio finale mostra una funzione che non è simmetrica. Se guardi il grafico, puoi accorgerti che nessuna porzione si "rispecchia" da un lato all'altro dell'asse delle ordinate o rispetto all'origine. Considera la funzione .[8]
- Seleziona alcuni varori per x e -x come segue:
- ; il punto è definito dalle coordinate (1,4);
- ; la coppia di valori è (-1,-2);
- ; le coordinate sono (2,10);
- ; il punto corrisponde a (2,-2).
- A questo punto, dovresti avere una quantità sufficiente di coppie per affermare che non vi è alcuna simmetria. I valori di y per le coppie opposte di x non sono identici né opposti; la funzione non è né pari né dispari.
- Forse puoi riconoscere questa funzione, , che può essere riscritta come . A prima vista potresti pensare che si tratti di una funzione pari perché ha solo un esponente pari; tuttavia, questo esempio dimostra che non puoi trarre delle conclusioni partendo dalla forma tra parentesi dell'equazione. Devi espanderla nei termini individuali ed esaminare in seguito ogni esponente.
Pubblicità - Seleziona alcuni varori per x e -x come segue:
Consigli
- Se tutte le variabili che compaiono nella funzione hanno esponenti pari, la funzione stessa è pari; se tutti gli esponenti sono dispari, lo è anche la funzione in generale.
Avvertenze
- Le istruzioni di questo articolo sono applicabili solamente alle funzioni con due variabili e che possono essere tracciate su un piano cartesiano bidimensionale.
Riferimenti
- ↑ http://www.purplemath.com/modules/fcnnot3.htm
- ↑ http://www.purplemath.com/modules/fcnnot3.htm
- ↑ http://www.purplemath.com/modules/fcnnot3.htm
- ↑ http://www.purplemath.com/modules/fcnnot3.htm
- ↑ https://www.mathsisfun.com/algebra/functions-odd-even.html
- ↑ https://www.mathsisfun.com/algebra/functions-odd-even.html
- ↑ https://www.mathsisfun.com/algebra/functions-odd-even.html
- ↑ https://www.mathsisfun.com/algebra/functions-odd-even.html







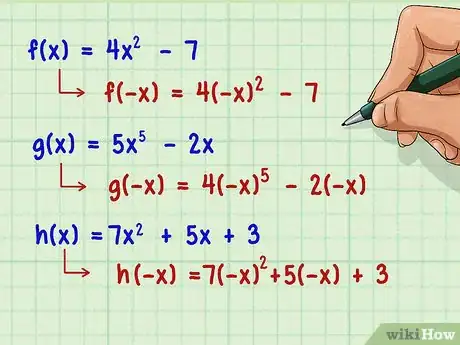






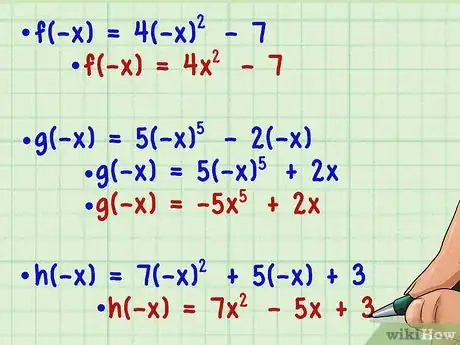





























-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 63 357 volte