Come Imparare la Trigonometria

Co-redatto da Lo Staff di wikiHow

La trigonometria è un ramo della matematica che studia i triangoli e i periodi. Le funzioni trigonometriche sono utilizzate per descrivere le proprietà di ogni angolo, delle relazioni fra i vari elementi dei triangoli e i grafici delle funzioni periodiche. Imparare la trigonometria aiuta a comprendere e visualizzare queste relazioni, i periodi e a tracciarne i relativi grafici. Se unisci lo studio a casa con un'attenzione costante in classe, potrai apprendere i concetti di base di questa materia e notare probabilmente le applicazioni delle funzioni periodiche nel mondo che ti circonda.

Parte 1

Parte 1 di 4:

Concentrarsi sui Concetti Trigonometrici Principali

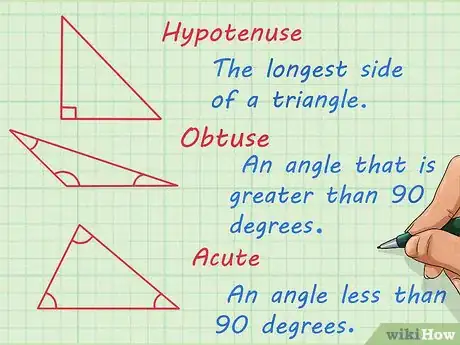
1
Definisci le parti di un triangolo. Il nucleo centrale della trigonometria è lo studio delle relazioni presenti fra gli elementi di un triangolo, che è una figura geometrica con tre lati e tre angoli. Per definizione, la somma degli angoli interni di un triangolo è pari a 180°. Dovresti prendere confidenza con questa figura e con la terminologia per riuscire a imparare la trigonometria. Ecco alcuni dei termini più comuni:^{[1]
X
Fonte di ricerca}
- Ipotenusa: il lato più lungo di un triangolo rettangolo;
- Ottuso: un angolo con ampiezza maggiore di 90°;
- Acuto: un angolo con ampiezza minore di 90°.
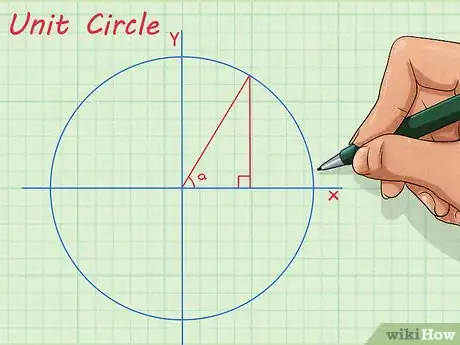
2
Impara a disegnare la circonferenza unitaria. Questa permette di ridimensionare in proporzione qualunque triangolo, in modo che la sua ipotenusa sia pari all'unità. Si tratta di un concetto importante, perché mette in relazione le funzioni trigonometriche, come il seno e il coseno, alle percentuali. Una volta compresa la circonferenza unitaria, puoi usare i valori trigonometrici di un dato angolo per risolvere i problemi in merito ai triangoli che lo contengono.^{[2]
X
Fonte di ricerca}
- Primo esempio; il seno di un angolo di 30° è 0,5; questo significa che il lato opposto a un angolo di 30° è esattamente la metà dell'ipotenusa.
- Secondo esempio: questa relazione può essere usata per trovare la lunghezza dell'ipotenusa in un triangolo con un angolo di 30°, in cui il lato opposto a tale angolo misura 7 cm. L'ipotenusa è uguale a 14 cm.
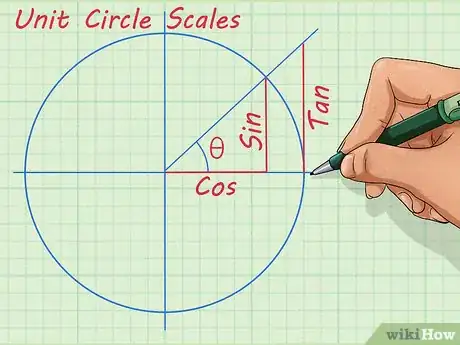
3
Impara le funzioni trigonometriche. Ci sono sei funzioni fondamentali per comprendere questa materia; tutte insieme sono in grado di definire le relazioni degli elementi di un triangolo e permettono di comprendere le caratteristiche peculiari di tale figura geometrica. Eccole:^{[3]
X
Fonte di ricerca}
- Seno (sin);
- Coseno (cos);
- Tangente (tg);
- Secante (sec);
- Cosecante (csec);
- Cotangente (ctg).
4
Ragiona sulle relazioni. Una delle cose più importanti da comprendere in merito alla trigonometria è che le funzioni sopra descritte sono tutte correlate fra loro. Sebbene i valori delle funzioni di seno, coseno, tangente e via dicendo abbiano le loro applicazioni specifiche, sono però i più utili a causa delle relazioni che esistono fra loro. La circonferenza unitaria è in grado di ridimensionare tali relazioni, in modo che siano facilmente comprensibili; quando riesci a padroneggiarla, puoi sfruttare le relazioni che descrive per dimostrare altri problemi.^{[4]
X
Fonte di ricerca}

Pubblicità

Parte 2

Parte 2 di 4:

Comprendere le Applicazioni della Trigonometria

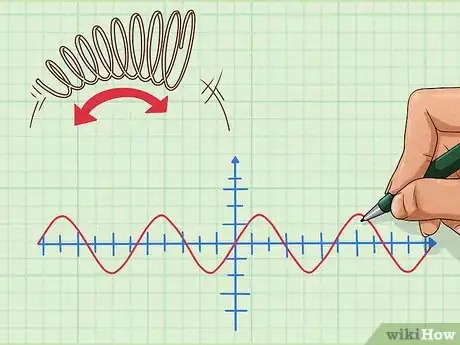
1
Comprendi gli utilizzi di base della trigonometria nel mondo accademico. Oltre a studiare questa materia per semplice amore verso la matematica, gli scienziati e i matematici applicano i concetti alla vita reale. La trigonometria permette di trovare i valori di angoli o segmenti lineari, può anche descrivere qualunque comportamento periodico rappresentandolo graficamente come una funzione trigonometrica.^{[5]
X
Fonte di ricerca}
- Ad esempio, il movimento di una molla che rimbalza avanti e indietro può essere descritto graficamente con un'onda sinusoidale.
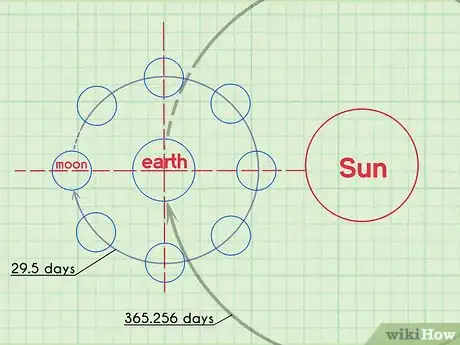
2
Pensa agli avvenimenti ciclici in natura. A volte, la gente ha difficoltà ad afferrare i concetti astratti della matematica o della scienza; se ti rendi conto che questi principi sono in verità presenti nel mondo reale, puoi spesso vederli sotto una luce diversa. Osserva le cose che si presentano in maniera ciclica e cerca di correlarle alla trigonometria.^{[6]
X
Fonte di ricerca}
- La luna segue un ciclo prevedibile che dura circa 29 giorni e mezzo.
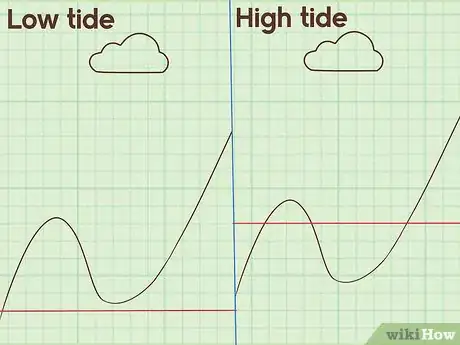
3
Visualizza come possono essere studiati gli eventi naturali ripetitivi. Quando ti accorgi che il mondo che ti circonda è ricco di questo tipo di fenomeni, inizia a riflettere su come potresti studiarli in maniera precisa. Considera l'aspetto del grafico che rappresenta questi cicli; a partire da esso puoi formulare un'equazione matematica per descrivere l'evento osservato. Questa analisi conferisce alla trigonometria un significato pratico che aiuta a comprendere meglio la sua utilità.^{[7]
X
Fonte di ricerca}
- Considera la misurazione della marea di una determinata spiaggia. Durante la fase di alta marea, l'altezza raggiunge il picco massimo per poi arrivare a quello minimo nelle ore di bassa marea. Dal livello più basso, l'acqua si sposta verso la spiaggia fino a raggiungere il livello più alto e questo ciclo si ripete in maniera infinita; può essere quindi rappresentato in un grafico come una funzione trigonometrica, nello specifico come una cosinusoide.
Pubblicità

Parte 3

Parte 3 di 4:

Studiare in Anticipo

1
Leggi il capitolo. I concetti trigonometrici sono spesso difficili da comprendere al primo tentativo; se leggi il capitolo del libro di testo prima che venga affrontato in classe, hai maggiore padronanza del contenuto. Più volte entri in contatto con la materia di studio e più collegamenti sei in grado di fare sulle varie relazioni presenti in trigonometria.^{[8]
X
Fonte di ricerca}
- Così facendo, puoi identificare gli argomenti con cui hai maggiori difficoltà prima della lezione.
2
Tieni un quaderno di appunti. Leggere il libro di testo è meglio di niente, ma questa materia non può essere appresa solo studiando approfonditamente i vari capitoli; scrivi degli appunti dettagliati dell'argomento che stai leggendo. Ricorda che la trigonometria è una materia "cumulativa", i concetti si sviluppano gli uni sugli altri, avere quindi gli appunti dei primi capitoli ti aiuta a comprendere meglio il contenuto di quelli successivi.^{[9]
X
Fonte di ricerca}
- Annota anche tutte le domande che vuoi porre al docente.
3
Risolvi i problemi del libro. Alcune persone sono in grado di visualizzare bene i concetti trigonometrici, ma altre incontrano parecchie difficoltà. Per essere certo di aver interiorizzato l'argomento, prova a risolvere alcuni problemi prima della lezione; in questo modo, se ti imbatti in passaggi poco chiari, sai già di quale tipo di aiuto avrai bisogno in classe.^{[10]
X
Fonte di ricerca}
- La maggior parte dei libri di testo fornisce le soluzioni dei problemi sul retro, per poter verificare il lavoro svolto.
4
Porta il materiale di studio a lezione. Avendo a disposizione gli appunti e i problemi pratici, puoi disporre di un punto di riferimento; così facendo, puoi anche ripassare gli argomenti che hai appreso e ricordare quelli per i quali hai bisogno di ulteriori spiegazioni. Accertati di chiarire ogni dubbio che hai elencato durante la lettura.

Pubblicità

Parte 4

Parte 4 di 4:

Prendere Appunti durante la Lezione

1
Usa lo stesso quaderno di appunti. I concetti di trigonometria sono tutti correlati. È meglio che tutte le note si trovino nello stesso posto per poter ripassare quelle precedenti. Scegli un quaderno o un raccoglitore ad anelli che usi solo per lo studio della trigonometria.^{[11]
X
Fonte di ricerca}
- Puoi usare il quaderno anche per risolvere i problemi.
2
Fai in modo che questa materia diventi la priorità durante le lezioni. Evita di utilizzare il tempo delle spiegazioni per socializzare o per svolgere i compiti di altre materie. Quando sei in classe, la mente dovrebbe essere completamente concentrata sulla lezione e sugli esercizi pratici; annota tutto quello che il docente scrive sulla lavagna o di cui sottolinea l'importanza.
3
Presta attenzione in classe. Offriti volontario per risolvere i problemi alla lavagna o condividi le tue soluzioni degli esercizi; se non hai capito qualcosa, fai delle domande. Mantieni la comunicazione aperta e fluida per quanto l'insegnante lo conceda; così facendo, puoi imparare e apprezzare meglio la trigonometria.
- Se il docente preferisce tenere una lezione frontale senza essere interrotto, risparmia le domande per le occasioni in cui puoi incontrarlo fuori dalla classe. Ricorda che insegnare la trigonometria è il suo lavoro, non essere timido e non temere di chiedere spiegazioni.
4
Continua a risolvere altri problemi pratici. Porta a termine tutti i compiti che vengono assegnati, perché sono degli ottimi indicatori per sapere quali saranno i quesiti dei compiti in classe. Se l'insegnante non dà esercizi da svolgere a casa, risolvi quelli proposti dal libro di testo e che fanno riferimento agli argomenti della lezione più recente.^{[12]
X
Fonte di ricerca}

Pubblicità

Consigli

Ricorda che la matematica è un modo di pensare e non solo una serie di formule da imparare.
Ripassa i concetti di algebra e geometria.

Avvertenze

Studiare all'ultimo minuto per un esame è una tecnica che raramente funziona con la trigonometria.
Non puoi imparare questa materia studiandola a memoria, devi comprendere i concetti correlati.