wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 57 542 volte
Una parte fondamentale nell’apprendimento dell’algebra consiste nell’imparare come trovare l'inverso di una funzione f (x), che viene denotata con f -1 (x) e visivamente è rappresentata dalla funzione originale riflessa rispetto alla retta y = x. Questo articolo ti mostrerà come trovare l'inverso di una funzione.
Passaggi
-
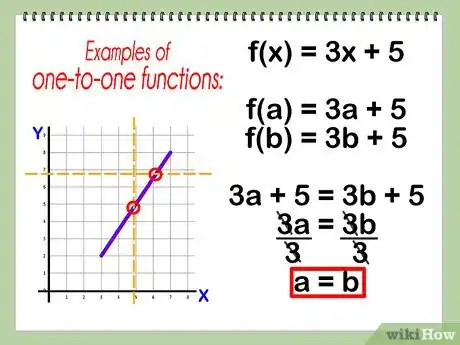
1Assicurati che la funzione sia “uno a uno”, cioè biunivoca. Solo queste funzioni hanno un inverso.
- Una funzione è biunivoca se passa il test della linea verticale e di quella orizzontale. Traccia una linea verticale attraverso l'intero grafico della funzione e contare il numero di volte che la linea taglia la funzione. Poi traccia una linea orizzontale attraverso l'intero grafico della funzione e conta il numero di volte che questa retta seca la funzione. Se ogni linea taglia solo una volta la funzione, la funzione è biunivoca.
- Se un grafico non passa il test della linea verticale, non si tratta nemmeno di una funzione.
- Per determinare algebricamente se la funzione è biunivoca, ponendo f (a) = f(b), si deve trovare che a = b. Ad esempio, prendiamo f (x) = 3 x + 5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- F (x) è così biunivoca.
- Una funzione è biunivoca se passa il test della linea verticale e di quella orizzontale. Traccia una linea verticale attraverso l'intero grafico della funzione e contare il numero di volte che la linea taglia la funzione. Poi traccia una linea orizzontale attraverso l'intero grafico della funzione e conta il numero di volte che questa retta seca la funzione. Se ogni linea taglia solo una volta la funzione, la funzione è biunivoca.
-
2Data una funzione, sostituisci le x con le y: ricordati che f (x) sta per "y".
- In una funzione, "f" o "y" rappresenta l'output e "x" rappresenta l'input. Per trovare l'inversa di una funzione, si invertono gli ingressi e le uscite.
- Esempio: prendiamo f (x) = (4x+3)/(2x+5), che è biunivoca. Commutando le x con le y, otteniamo x = (4y + 3) /(2y + 5).
-
3Risolvi rispetto alla nuova "y". Sarà necessario modificare le espressioni per risolvere rispetto a y o per trovare le nuove operazioni che devono essere eseguite in ingresso per ottenere l'inverso come uscita.
- Questo può essere difficile a seconda della tua espressione. Potrebbe essere necessario utilizzare trucchi algebrici come la moltiplicazione incrociata o la fattorizzazione per valutare l'espressione e semplificarla.
- Nel nostro esempio, seguiremo i passaggi seguenti per isolare y:
- Stiamo iniziando con x = (4y + 3) /(2y + 5)
- x (2y + 5) = 4y + 3 – Moltiplica entrambi i lati per (2y + 5)
- 2xy + 5x = 4y + 3 – Moltiplica per x
- 2xy - 4y = 3-5 x — Metti tutti i termini y da una parte
- y(2x - 4) = 3 - 5x – Raccogli la y
- y = (x 3-5) / (2 x - 4) – Dividi per ottenere la tua risposta
-
4Rimpiazza la nuova "y" con f -1 (x). Questa è l'equazione per l'inversa della funzione originale.
- La nostra risposta finale è f -1 (x) = (3-5 x) / (2x - 4). Questa è la funzione inversa di f (x) = (4x+3)/(2x+5).
Pubblicità
Riferimenti
Informazioni su questo wikiHow
Per trovare l'inverso di una funzione, inizia scambiando x e y. Poi, risolvi semplicemente l'equazione per la nuova y. Per esempio, se hai la funzione f(x) = (4x+3)/(2x+5), prima devi scambiare la x e la y, ottenendo x = (4y+3)/(2y+5). Poi, risolvi per y, trovando (3-5x)/(2x-4), cioè l'inverso della funzione originale. Per imparare a determinare se una funzione è invertibile, continua a leggere!

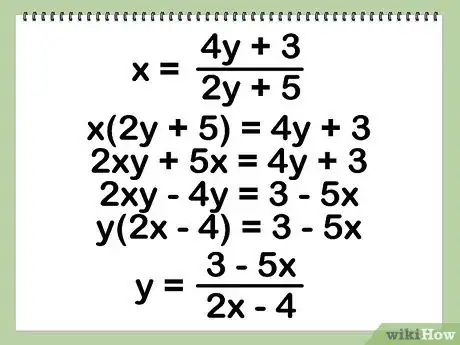




-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
