wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 23 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 51 300 volte
Forse stai cercando di rispondere a una domanda come "Se una camicetta che originariamente costa € 45 è in vendita al 20% di sconto, qual è il suo nuovo prezzo?" Questi tipi di domande sono dette “aumento/diminuzione in percentuale” e sono un nodo abbastanza basilare di matematica.Con un piccolo aiuto, è possibile risolverle facilmente e quasi istintivamente.
Passaggi
Metodo Uno: Perfetta Percentuale
-
1Usa il metodo di percentuale perfetta per i seguenti tipi di problemi: “Se una camicia che costa € 40 è ridotta a 32, qual è la percentuale di sconto applicata?"
-
2Decidi quale numero rappresenta la quantità originale e quale rappresenta la "quantità nuova". L'importo che esiste dopo che è stata applicata la percentuale può essere chiamato anche "nuovo importo".
- Per la nostra domanda, non sappiamo la percentuale. Sappiamo che € 40 è l’importo originale e che il 32 è il "dopo".
-
3Dividi il "dopo" per l'importo originale. Assicurati che la quantità "dopo" vada nella calcolatrice per prima.
- Per il nostro esempio, scrivi 32 diviso 40 e premi l’uguale.
- Questa divisione ci dà 0,8. Non è la risposta finale.
-
4Sposta il punto decimale di due posti a destra per cambiare da numero decimale a percentuale. Per il nostro problema di esempio, 0,8 si cambia in 80%.
-
5Confronta tale percentuale con il 100%. Se la risposta è inferiore a 100%, si ha una diminuzione o sconto; maggiore di 100% è un aumento.
- Poiché il prezzo nell'esempio è sceso e il prezzo che abbiamo calcolato è anche uno sconto, siamo sulla strada giusta.
- Il prezzo nell'esempio è sceso da € 40 a € 32: se, tuttavia, avessimo ottenuto 120% dopo il nostro calcolo, sapremmo di aver sbagliato qualcosa, perché siamo alla ricerca di uno sconto e avremmo invece ottenuto un aumento.
-
6Confronta la percentuale con il 100%. Cerca di capire quanto sei sopra o sotto il 100% e questa sarà la risposta finale. Nel nostro problema 80% rispetto a 100% significa che abbiamo avuto uno sconto del 20%.
-
7Fai pratica sui seguenti esempi. Prova a vedere se riesci a finire i seguenti problemi:
- Problema 1:
“Una camicetta da € 50 ora è scesa a 28. Qual era la percentuale di sconto?“- Per risolverlo, prendi una calcolatrice. Immetti “28 : 50 =” e la risposta è 0,56.
- Converti 0,56 in 56 %. Confronta questo numero con il 100%, sottraendo 56 da 100, ottenendo uno sconto del 44%.
- Problema 2:
“Un berretto da baseball da12 euro costa15 al lordo delle imposte. Qual è la percentuale di tasse applicate?”- Per risolverlo, prendi una calcolatrice. Scrivi “15 : 12 =” e la risposta è 1,25.
- Converti 1,25 in 125 %. Paragona questo con i 100%, sottraendo 100 da 125 e trovando un aumento del 25%.
Pubblicità - Problema 1:
Metodo Due: Nuovo Importo Sconosciuto
-
1Usa il nuovo metodo di quantità sconosciute per i seguenti tipi di problemi: "Un paio di jeans costa 25 euro ed è in vendita scontato al 60%. Qual è il prezzo di vendita?"' o “Una colonia di 4.800 batteri cresce del 20%. Quanti batteri ci sono ora?”
-
2Decidi se hai un aumento o una diminuzione della situazione iniziale. Qualcosa di simile a una tassa di vendita, ad esempio, è una situazione di aumento. Uno sconto, d'altra parte, è una situazione di diminuzione.
-
3Se si ha una situazione di aumento, aggiungi la tua percentuale a 100. Quindi un 8% di tassa diventa 108%, ad esempio, o una maggiorazione del 12% diventa 112%.
-
4Se si ha una situazione di diminuzione, devi sottrarre la percentuale da 100. Se qualcosa è al 30% in meno, si lavora con il 70%; se qualcosa è scontato al 12%, si tratta di un 88%.
-
5Converti la risposta al Passaggio 3 o 4 in numero decimale. Questo significa spostare il punto decimale di due posti a sinistra.
- Per esempio, 67% diventa 0,67; 125% diventa 1,25; 108% diventa 1,08; ecc.
- Se non sei sicuro di come fare questo calcolo, puoi anche dividere la percentuale per 100. Questo ti darà lo stesso numero.
-
6Moltiplica questo decimale per il tuo importo originale. Se, ad esempio, stiamo lavorando sul problema “Un paio di jeans da 25 euro è in vendita scontato del 60%. Qual è il prezzo di vendita?"', la seguente è un'illustrazione di questo passaggio:
- 25 x 0,40 = ?
- Ricorda che abbiamo sottratto il nostro prezzo di vendita del 60% da 100, ottenendo il 40%, e poi l’abbiamo trasformato in un numero decimale.
-
7Etichetta l'aumento o la diminuzione in modo appropriato e hai finito. Nel nostro esempio, avevamo:
- 25 x 0,40 = ? Moltiplica i due numeri insieme e abbiamo ottenuto 10.
- Ma 10 che cosa? 10 euro, quindi diciamo che il nuovo jeans costa € 10 dopo lo sconto del 60%.
-
8Fai pratica sui seguenti esempi. Per comprendere meglio questo tipo di problema, cerca di vedere se capisci come finire i seguenti problemi:
- Problema 1:
“Un paio di jeans da 120 euro è in vendita al 65% di sconto. Qual è il prezzo di vendita?”- Per risolvere:
100 - 65 dà 35%; 35% si converte in 0,35. - 0,35 x 120 equivale a 42; il nuovo prezzo è € 42.
- Per risolvere:
- Problema 2:
“Una colonia di 4.800 batteri cresce del 20%. Quanti batteri ci sono ora?”- Per risolvere: 100 + 20 dà 120% che si converte in 1,2.
- 1,2 x 4.800 equivale a 5.760; ora ci sono 5.760 batteri nella colonia.
Pubblicità - Problema 1:
Metodo Tre: Quantità Originale Sconosciuta
-
1Usa il metodo originale sulla quantità sconosciuta per i seguenti tipi di problemi: “Un videogioco è in vendita al 75% di sconto. Il prezzo di svendita è di € 15. Qual era il prezzo originale?” oppure “Un investimento è cresciuto del 22% e ora vale € 1.525. Quanto era stato investito originariamente?”
- Per risolvere queste domande, è necessario comprendere che le percentuali sono applicate mediante moltiplicazione. Se è un aumento o diminuzione, è stato applicato mediante moltiplicazione. Il tuo compito, quindi, è di annullare tale moltiplicazione. Devi annullare l'applicazione della percentuale. Dunque, tre cose saranno vere:
- Dividerai per la percentuale.
- Se hai un aumento, aggiungerai la percentuale a 100.
- Se hai una diminuzione, sottrarrai la percentuale da 100.
- Per risolvere queste domande, è necessario comprendere che le percentuali sono applicate mediante moltiplicazione. Se è un aumento o diminuzione, è stato applicato mediante moltiplicazione. Il tuo compito, quindi, è di annullare tale moltiplicazione. Devi annullare l'applicazione della percentuale. Dunque, tre cose saranno vere:
-
2Decidi se si tratta di una situazione di aumento o diminuzione. L’imposta sulle vendite, per esempio, è un aumento; gli sconti sono una diminuzione. Un investimento che cresce in valore è un aumento; una popolazione che scende di numero è una diminuzione e così via.
- Immaginiamo di dover risolvere il seguente problema:
“Un video è in vendita scontato del 75%. Il prezzo di svendita è di € 15. Qual è il prezzo originale?” - Svendita è un'altra parola per sconto, così abbiamo a che fare con una diminuzione.
- € 15 è la nostra quantità “dopo”, perché è il numero che abbiamo “dopo” la svendita.
- Immaginiamo di dover risolvere il seguente problema:
-
3Se si tratta di un aumento, aggiungi la percentuale al 100. Se si tratta di una diminuzione, sottrai la percentuale da 100.
- Poiché abbiamo a che fare con un riduzione/sconto, sottrai 100 - 75, ottenendo 25%.
-
4Converti tale numero in decimale. Fai questo spostando la virgola di due posti a sinistra o dividendo il numero per 100.
- 25% diventa 0,25.
-
5Dividi il "dopo" per i decimali del Passaggio 3. Questo ti aiuterà a invertire la moltiplicazione di cui abbiamo parlato nel Passaggio 1.
-
6Il nostro "dopo importo" è di € 15 e il nostro decimale è pari a 0,25. Prendi una calcolatrice: “15 : 0,25 =”.
-
7Etichetta in modo appropriato e hai finito. Hai appena calcolato il prezzo originale.
- 15 diviso 0,25 = 60, che significa che il prezzo originale era di € 60.
- Se desideri controllare la tua risposta per assicurarti che sia corretta, moltiplica il prezzo di vendita (75% o 0,75) per il prezzo originale (€ 60) e vedi se si ottiene il prezzo di vendita.
- (€ 15) : 0,75 x 60 = Vendita di € 45; € 60 (prezzo originale) - € 45 (importo sconto) = € 15 (prezzo di vendita)
-
8Fai pratica sui seguenti esempi. Per meglio comprendere questo tipo di problema, cerca di capire come finire il seguente problema: “Un investimento è cresciuto del 22% e ora vale € 1.525. Quanto era stato investito originariamente?”
- Questa è una situazione di aumento, quindi, calcola 100 + 22.
- Converti la risposta in numero decimale: 122% diventa 1,22
- Su una calcolatrice, immetti “1.525 : 1,22 =”.
- Segnati la risposta. Per questo problema, 1.525 : 1,22 = 1250, così l'investimento iniziale è stato di € 1.250.
Pubblicità
Consigli
- Se non conosci il nuovo importo, potrai moltiplicare. In caso contrario, potrai dividere.
- Ricorda ad esempio le unità, euro, dollari, sterline o % ecc. Con diverse operazioni, otterrai sempre queste stesse unità.
- Se si tratta di un aumento, aggiungi la percentuale a 100; se si tratta di una diminuzione, sottraila da 100. Questo è vero indipendentemente dal fatto che si stia moltiplicando o dividendo.
- Non dimenticare la virgola decimale.
Avvertenze
- L’ordine della divisione è cruciale! Assicurati di mettere l'importo corretto nella calcolatrice per primo.
Cose che ti Serviranno
- Una calcolatrice.



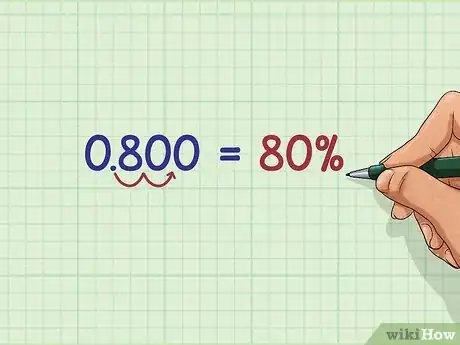
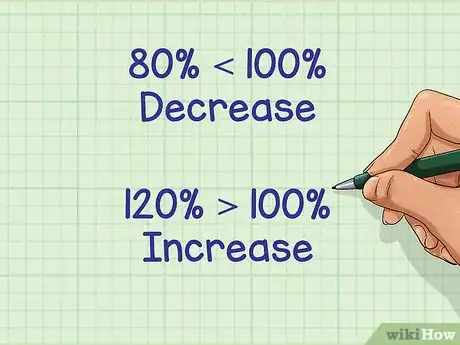
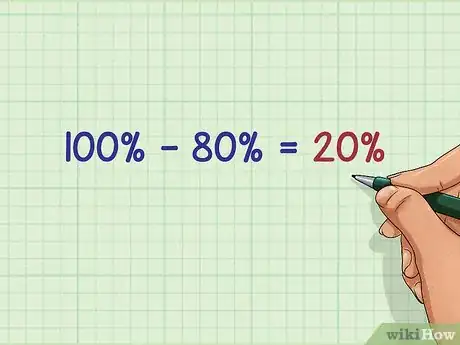






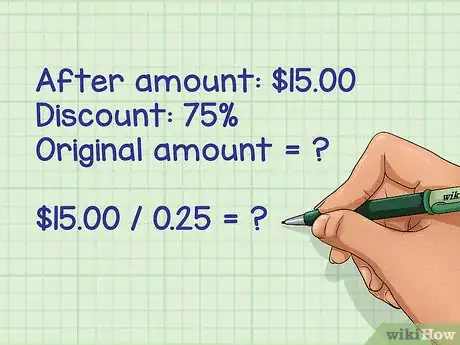





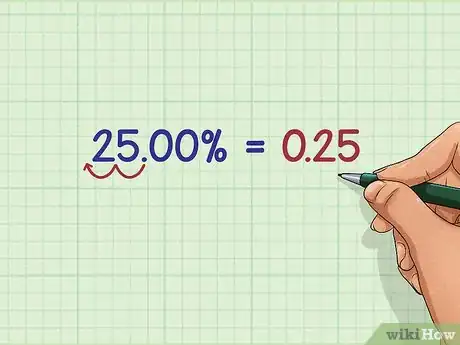
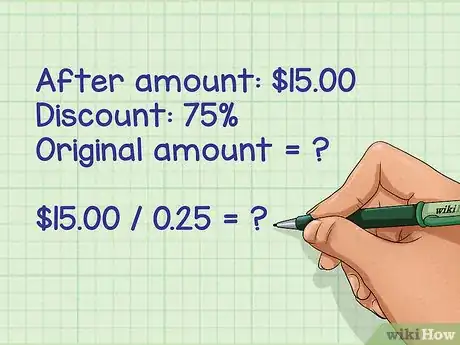
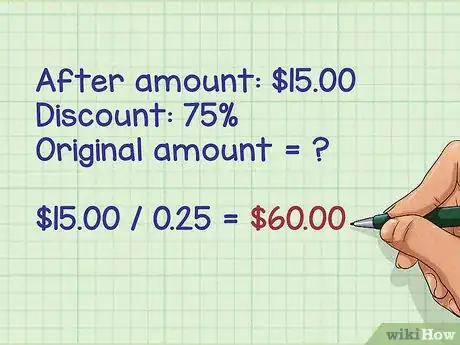


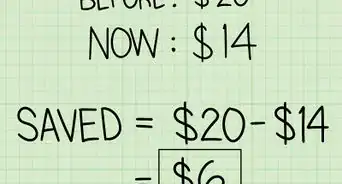
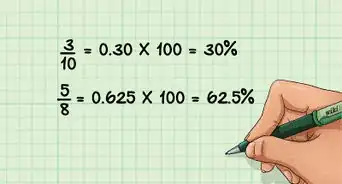



-to-Grams-(g)-Step-12-Version-4.webp)