wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 3 658 volte
I numeri interi sono numeri positivi o negativi senza frazioni o decimali. Moltiplicare e dividere 2 o più numeri interi non è molto diverso rispetto alle stesse operazioni sui numeri solo positivi. La differenza sostanziale è rappresentata dal segno meno, di cui bisogna sempre tener conto. Tenendo conto del segno, puoi procedere alla moltiplicazione normalmente.
Passaggi
Informazioni generali
-
1Impara a riconoscere i numeri interi. Un intero è un numero tondo che può essere rappresentato senza frazioni o decimali. Gli interi possono essere positivi, negativi o nulli (0). Per esempio, questi numeri sono interi: 1, 99, -217 e 0. Mentre questi non lo sono: -10.4, 6 ¾, 2.12.
- I valori assoluti possono essere interi, ma non lo sono per forza. Un valore assoluto di qualsiasi numero è la “dimensione” o “quantità” del numero, a prescindere dal segno. Un altro modo per renderlo è che il valore assoluto di un numero è la distanza di questo dallo 0. Perciò, il valore assoluto di un intero è sempre un intero. Per esempio, il valore assoluto di -12 è 12. Il valore assoluto di 3 è 3. Di 0 è 0.
- I valori assoluti di numeri non interi, tuttavia, non saranno mai interi. Per esempio, il valore assoluto di 1/11 è 1/11 – una frazione, quindi non un intero.
- I valori assoluti possono essere interi, ma non lo sono per forza. Un valore assoluto di qualsiasi numero è la “dimensione” o “quantità” del numero, a prescindere dal segno. Un altro modo per renderlo è che il valore assoluto di un numero è la distanza di questo dallo 0. Perciò, il valore assoluto di un intero è sempre un intero. Per esempio, il valore assoluto di -12 è 12. Il valore assoluto di 3 è 3. Di 0 è 0.
-
2Impara le tabelline di base. Il processo di moltiplicazione e divisione degli interi, che siano grandi o piccoli, è molto molto più semplice e veloce dopo aver memorizzato i prodotti di ogni coppia di numeri tra 1 e 10. Quest’informazione è solitamente insegnata a scuola come “tabelline”. Come promemoria, è riportata di seguito la tabellina 10x10. I numeri nella prima riga e nella prima colonna vanno da 1 a 10. Per trovare il prodotto di una coppia di numeri, individua l’intersezione tra la colonna e la riga dei numeri in questione:Pubblicità
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Moltiplicare i numeri interi
-
1Conta i segni meno all’interno del problema di moltiplicazione. Un problema comune tra due o più numeri positivi darà sempre un risultato positivo. Tuttavia, ogni segno negativo aggiunto a una moltiplicazione trasforma il segno finale da positivo a negativo o viceversa. Per iniziare un problema di moltiplicazione intero, conta i segni negativi.
- Usiamo l’esempio -10 × 5 × -11 × -20. In questo problema, possiamo chiaramente vedere tre meno. Useremo questo dato nel prossimo punto.
-
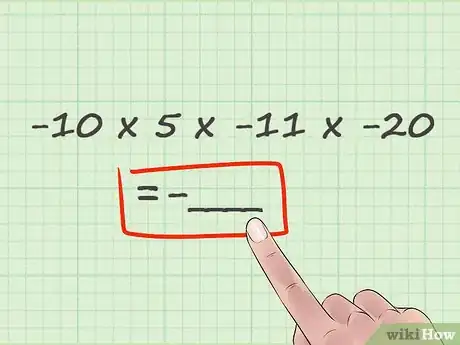
2Stabilisci il segno della tua risposta in base al numero di segni negativi nel problema. Come notato in precedenza, la risposta a una moltiplicazione con soli segni positivi sarà positiva. Per ogni meno nel problema, inverti il segno della risposta. In altre parole, se il problema ha un solo segno negativo, la risposta sarà negativa; se ne ha due, sarà positiva e così via. Una buona regola è che i numeri dispari di segni negativi danno risultati negativi e i numeri pari di segni negativi danno risultati positivi.
- Nel nostro esempio, abbiamo tre segni negativi. Tre è dispari, perciò sappiamo che la risposta sarà negativa. Possiamo mettere un meno nello spazio della risposta, così: -10 × 5 × -11 × -20 = -__
-
3Moltiplica i numeri da 1 a 10 usando le tabelline. Il prodotto di due numeri minori o uguali a 10 è incluso nelle tabelline di base (vedi sopra). Per questi semplici casi, basta scrivere la risposta. Ricorda che, nei problemi con solo moltiplicazioni, puoi spostare gli interi come sei più comodo per moltiplicare tra loro i numeri semplici.
- Nel nostro esempio, 10 × 5 è incluso nelle tabelline. Non dobbiamo tener conto del segno meno sul 10 perché abbiamo già trovato il segno della risposta. 10 × 5 = 50. Possiamo inserire questo risultato nel problema così: (50) × -11 × -20 = -__
- Se stai avendo difficoltà a visualizzare problemi basilari di moltiplicazione, pensali come addizioni. Per esempio, 5 × 10 è come dire “10 volte 5”. In altre parole, 5 × 10 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5.
- Nel nostro esempio, 10 × 5 è incluso nelle tabelline. Non dobbiamo tener conto del segno meno sul 10 perché abbiamo già trovato il segno della risposta. 10 × 5 = 50. Possiamo inserire questo risultato nel problema così: (50) × -11 × -20 = -__
-
4Se necessario, scomponi numeri più grandi in pezzi più semplici. Se la tua moltiplicazione riguarda numeri più grandi di 10, non devi per forza usare la moltiplicazione lunga. Innanzitutto, vedi se puoi scomporre uno o più numeri in pezzetti più gestibili. Poiché, con le tabelline, puoi risolvere semplici problemi di moltiplicazione quasi immediatamente, ridurre un problema difficile in tanti facili problemi è solitamente più semplice rispetto alla soluzione del singolo problema complesso.
- Passiamo alla seconda parte dell’esempio, -11 × -20. Possiamo omettere i segni perché abbiamo già ricavato il segno della risposta. 11 × 20 sembra complicato, ma riscrivendo il problema come 10 × 20 + 1 × 20, all’improvviso è molto più gestibile. 10 × 20 è solo 2 volte 10 × 10, o 200. 1 × 20 è solo 20. Sommando i risultati, otteniamo 200 + 20 = 220. Possiamo reinserirlo nel problema in questo modo: (50) × (220) = -__
-
5Per numeri più complessi, usa la moltiplicazione lunga. Se il tuo problema comprende due o più numeri maggiori di 10 e non riesci a trovare la risposta scomponendo il problema in parti più fattibili, puoi comunque risolvere tramite moltiplicazione lunga. In questo tipo di moltiplicazione, allinei le tue risposte come faresti in un addizione e moltiplichi ogni cifra nel numero in fondo con ogni cifra di quello in cima. Se il numero inferiore ha più di una cifra, devi tener conto delle cifre nelle decine, centinaia e così via aggiungendo zeri a destra della tua risposta. Infine, per ottenere la risposta finale, somma tutte le risposte parziali.
- Torniamo al nostro esempio. Ora, dobbiamo moltiplicare 50 per 220. Sarà difficile da scomporre in pezzi più facili, perciò usiamo la moltiplicazione lunga. I problemi a moltiplicazione lunga sono più facili da gestire se il numero più piccolo è sul fondo, perciò scriviamo il problema con 220 sopra e 50 sotto.
- Per prima cosa moltiplica la cifra nelle unità in basso per ciascuna cifra del numero superiore. Poiché 50 è sotto, 0 è la cifra nelle unità. 0 × 0 fa 0, 0 × 2 fa 0, e 0 × 2 fa zero. In altre parole, 0 × 220 fa zero. Scrivilo sotto la moltiplicazione lunga nelle unità. Questa è la nostra prima risposta parziale.
- Poi, moltiplicheremo la cifra nelle decine del numero inferiore per ogni cifra del numero superiore. 5 è la cifra nelle decine in 50. Poiché questo 5 è nelle decine invece che nelle unità, scriviamo uno 0 sotto la nostra prima risposta parziale nelle unità prima di proseguire. Poi, moltiplichiamo. 5 × 0 fa 0. 5 × 2 a 10, perciò scrivi 0 e aggiungi 1 al prodotto di 5 e la cifra successiva. 5 × 2 fa 10. Solitamente, scriveremmo 0 e riporteremmo l’1, ma in questo caso aggiungiamo anche l’1 dal problema precedente, ottenendo 11. Scrivi “1”. Riportando l’1 dalle decine di 11, vediamo che non abbiamo più cifre, perciò lo scriviamo semplicemente sulla sinistra della nostra risposta parziale. Registrando tutto questo, ci resta 11000.
- Ora, non facciamo altro che sommare. 0 + 11000 fa 10000. Poiché sappiamo che la risposta al nostro problema originale è negativa, possiamo stabilire con certezza che -10 × 5 × -11 × -20 = -11000.
Pubblicità - Torniamo al nostro esempio. Ora, dobbiamo moltiplicare 50 per 220. Sarà difficile da scomporre in pezzi più facili, perciò usiamo la moltiplicazione lunga. I problemi a moltiplicazione lunga sono più facili da gestire se il numero più piccolo è sul fondo, perciò scriviamo il problema con 220 sopra e 50 sotto.
Dividere i numeri interi
-
1Come prima, stabilisci il segno della tua risposta basandoti sul numero di segni meno nel problema. Introdurre la divisione in un problema matematico non cambia le regole riguardo ai segni negativi. Se c’è un numero dispari di segni negativi, la risposta è negativa, se è pari (o nullo) la risposta sarà positiva.
- Usiamo un esempio comprendente sia moltiplicazioni che divisioni. Nel problema -15 × 4 ÷ 2 × -9 ÷ -10, ci sono tre segni meno, perciò la risposta sarà negativa. Come prima, possiamo mettere un segno meno al posto della nostra risposta, così: -15 × 4 ÷ 2 × -9 ÷ -10 = -__
-
2Fai semplici divisioni usando la tua conoscenza delle moltiplicazioni. La divisione può essere pensata come una moltiplicazione a ritroso. Quando dividi un numero per un altro, ti stai chiedendo “quante volte il secondo numero è incluso nel secondo?” o, in altre parole, “per cosa devo moltiplicare il secondo numero per ottenere il primo?”. Vedi le tabelline di base 10x10 per avere un riferimento – se ti viene chiesto di dividere una delle risposte nelle tabelline per qualsiasi numero da 1 a 10, sai che la risposta è semplicemente l’altro numero da 1 a 10 a cui è necessario moltiplicare n per ottenerlo.
- Prendiamo il nostro esempio. In -15 × 4 ÷ 2 × -9 ÷ -10, troviamo 4 ÷ 2. 4 è una risposta nelle tabelline - sia 4 × 1 che 2 × 2 danno 4 come risposta. Poiché ci viene chiesto di dividere 4 per 2, sappiamo che stiamo sostanzialmente risolvendo il problema 2 × __ = 4. Nello spazio, ovviamente, scriveremo 2, in modo che 4 ÷ 2 = 2. Riscriviamo il nostro problema come -15 × (2) × -9 ÷ -10.
-
3Usa la divisione lunga dove necessario. Come per la moltiplicazione, quando t’imbatti in una divisione troppo difficile da risolvere mentalmente o con le tabelline, hai la possibilità di risolverla con un approccio lungo. In una divisione lunga, scrivi i due numeri in una parentesi speciale a forma di L, poi dividi cifra per cifra, spostando le risposte parziali verso destra man mano che procedi per tener conto del valore decrescente delle cifre che stai dividendo – centinaia, poi decine, poi unità e così via.
- Usiamo la divisione lunga nel nostro esempio. Possiamo semplificare -15 × (2) × -9 ÷ -10 in 270 ÷ -10. Ignoreremo i segni come al solito perché conosciamo il segno finale. Scrivi 10 a sinistra e poni 270 sotto di essa.
- Iniziamo dividendo la prima cifra del numero sotto la parentesi per il numero a lato. La prima cifra è 2 è il numero a lato è 10. Poiché 10 non è incluso nel 2, useremo piuttosto le prime due cifre. Il 10 sta nel 27 – due volte. Scrivi "2" sopra il 7 sotto la parentesi. 2 è la prima cifra nella tua risposta.
- Ora, moltiplica il numero a sinistra della parentesi per la cifra appena scoperta. 2 × 10 fa 20. Scrivilo sotto le prime due cifre del numero sotto la parentesi – in questo caso, 2 e 7.
- Sottrai i numeri appena scritti. 27 meno 20 fa 7. Scrivilo sotto al problema.
- Passa alla cifra successiva del numero sotto la parentesi. La prossima cifra in 270 è 0. Riportala di fianco al 7 per ottenere 70.
- Dividi il nuovo numero. Poi, dividi 10 per 70. 10 è incluso esattamente 7 volte nel 70, perciò scrivilo sopra di fianco al 2. Questa è la seconda cifra della risposta. La risposta finale è 27.
- Nota che, nel caso in cui il 10 non fosse stato divisibile perfettamente nel numero finale, avremmo dovuto tener conto della quota di 10 avanzata – il resto. Per esempio, se il nostro ultimo compito fosse dividere 71, invece che 70, per 10, noteremmo che 10 non è perfettamente incluso nel 71. Ci sta 7 volte, ma avanza un’unità (1). In altre parole, possiamo includere sette 10 e un 1 nel 71. Scriveremmo quindi la nostra risposta come "27 con resto di 1" o "27 r1".
Pubblicità - Usiamo la divisione lunga nel nostro esempio. Possiamo semplificare -15 × (2) × -9 ÷ -10 in 270 ÷ -10. Ignoreremo i segni come al solito perché conosciamo il segno finale. Scrivi 10 a sinistra e poni 270 sotto di essa.
Consigli
- Nella moltiplicazione si può variare l’ordine dei fattori, e possono essere raggruppati. Perciò un problema come 15x3x6x2 può essere riscritto come 15x2x3x6 o (30)x(18).
- Ricorda che un problema come 15x2x0x3x6 sarà uguale a 0. Non devi calcolare nulla.
- Occhio all’ordine delle operazioni. Queste regole si applicano a ogni gruppo di moltiplicazioni e/o divisioni, ma non a sottrazioni o addizioni.



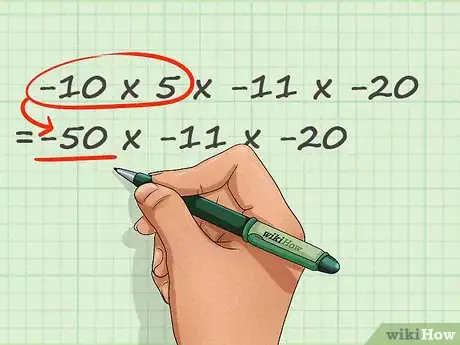
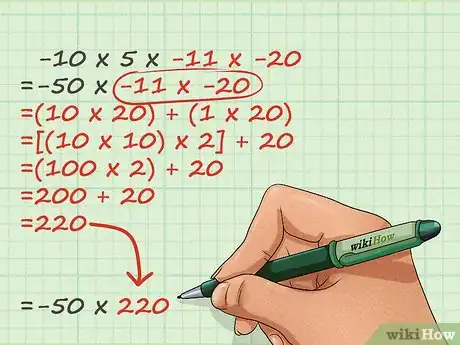
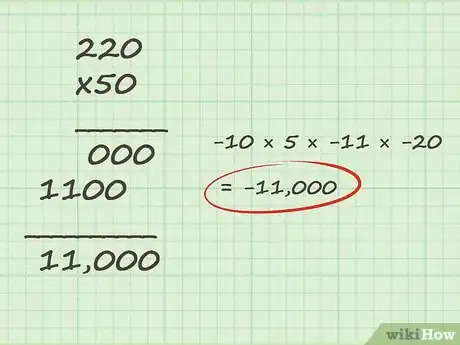
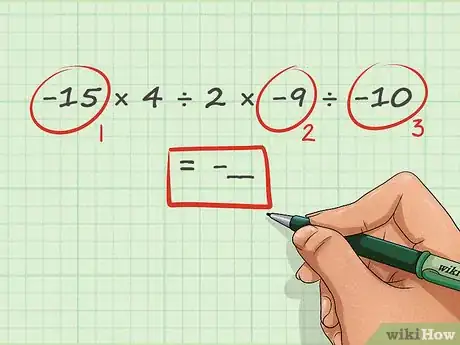
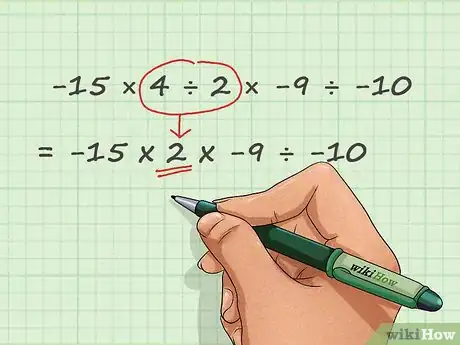
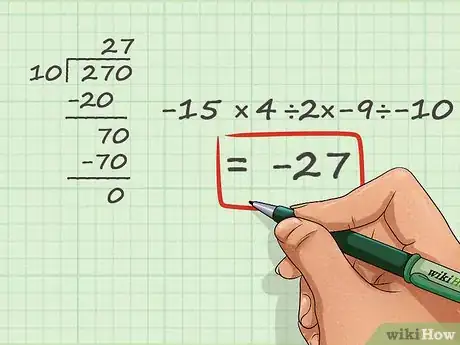



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
