X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 11 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 11 984 volte
Saper ridurre una matrice è molto utile in molteplici applicazioni. Questa procedura può essere usata per risolvere sistemi di equazioni lineari, interpretare geometricamente vettori diversi fra loro o per individuare alcune proprietà della matrice stessa, come il determinante.
Passaggi
-
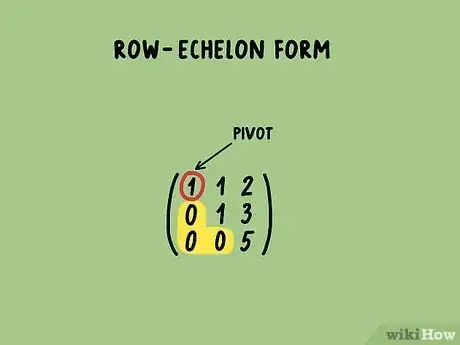
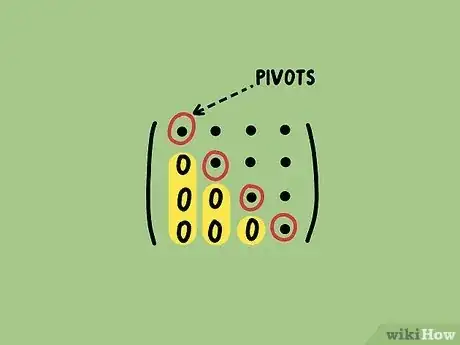
1Comprendi quando una matrice è ridotta per righe (anche conosciuta come "matrice a scalini"). Si dice matrice a scalini la matrice in cui il primo elemento non nullo di ogni riga presenta il valore zero nella stessa posizione della riga sottostante. All'interno di una matrice a scalini il primo elemento non nullo di ogni riga prende il nome di "pivot" e l'analisi della relazione esistente fra i pivot e la loro posizione all'interno della matrice fornisce molte informazioni utili relative alla matrice stessa. Di seguito trovi un esempio di matrice a scalini:
-
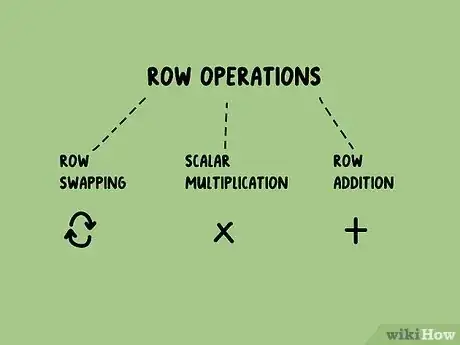
2Comprendi come si eseguono le operazioni elementari sulle righe di una matrice. Le operazioni eseguibili sulle righe di una matrice sono essenzialmente tre:
- Scambio di righe;
- Moltiplicazione scalare. Qualsiasi riga della matrice può essere sostituita con un multiplo scalare non nullo di se stessa;
- Somma. Una riga di una matrice può essere sostituita dalla somma di se stessa con un multiplo di un'altra riga.
-
3Inizia riportando la matrice che vuoi ridurre.
-
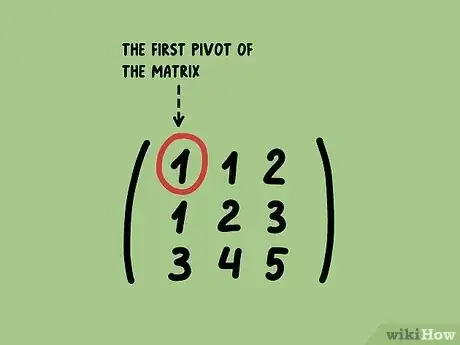
4Identifica il primo pivot della matrice. Gli elementi pivot di una matrice sono fondamentali per poter capire come eseguire il processo di riduzione. Quando una matrice è stata ridotta tutti gli elementi elencati sotto a ciascun pivot devono essere pari a 0.
- Nella matrice di esempio il primo pivot è l'elemento che occupa la prima posizione in alto a sinistra. Normalmente è sempre così, a meno che il primo elemento della matrice, quello collocato in alto a sinistra, non sia pari a 0. In quest'ultimo caso, scambia le righe della matrice finché il primo elemento non è diverso da zero.
- Per definizione all'interno di ogni riga e di ogni colonna della matrice può essere presente un solo pivot. Dopo aver selezionato il primo elemento della matrice (quello che occupa la prima posizione in alto a sinistra) come pivot, nessuno degli altri elementi presenti nella riga e nella colonna corrispondente potranno essere dei pivot.
-
5Esegui tutte le operazioni necessarie per fare in modo che tutti gli elementi posti sotto al primo pivot diventino pari a 0.
- Nella matrice di esempio, hai la necessità che i valori che compaiono sotto al primo pivot siano tutti pari a 0. Sostituisci la seconda riga con il risultato della sottrazione della prima riga dalla seconda. A questo punto sostituisci la terza riga con il risultato della sottrazione della prima riga da se stessa per tre volte. Queste due operazioni possono essere riassunte e descritte in questo modo e
-
6Individua il secondo pivot della matrice di esempio. In questo caso puoi scegliere sia l'elemento centrale della seconda riga sia l'elemento centrale della terza riga, ma non può essere l'elemento centrale della prima riga, dato che quest'ultima contiene già un pivot. In questo esempio viene scelto come pivot l'elemento centrale della seconda riga, anche se nessuno vieta di scegliere quello centrale della terza riga.
-
7Esegui tutte le operazioni necessarie sulle righe della matrice affinché tutti i valori presenti sotto al secondo pivot siano pari a 0.
- La matrice che hai ottenuto è una matrice ridotta correttamente per righe.
-
8In linea generale, se la matrice che stai studiando ha una dimensione maggiore di quella di esempio, dovrai continuare a selezionare gli elementi pivot, finché sarà possibile, e fare in modo che tutti gli elementi a loro sottostanti diventino pari a 0.Pubblicità
Consigli
- Qualsiasi tipo di matrice, indipendentemente dalle sue dimensioni (quadrata o rettangolare), può essere ridotta.
Pubblicità
Informazioni su questo wikiHow
Pubblicità



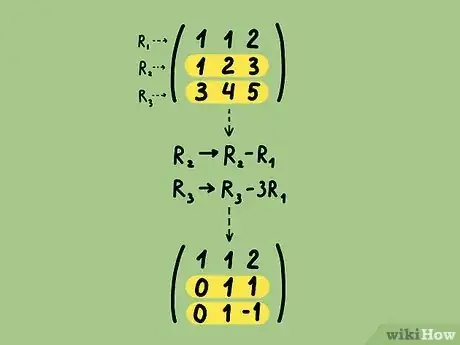




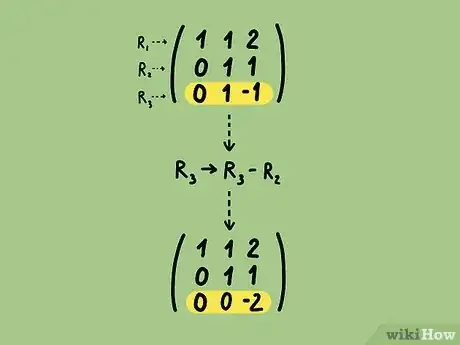





-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
