X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 12 325 volte
Un'equazione trigonometrica è un'equazione che contiene una o più funzioni trigonometriche della variabile x. Risolvere per x significa trovare i valori della x che inseriti all'interno della funzione trigonometrica la soddisfano.
- Le soluzioni o i valori delle funzioni di arco, sono espresse in gradi o in radianti. Ad esempio: x = π/3 ; x = 5π/6 ; x = 3π2 ; x = 45 deg. ; x = 37,12 deg. ; x = 178,37 deg.
- Nota: sul cerchio trigonometrico unitario, le funzioni trigonometriche di ogni arco sono le stesse funzioni trigonometriche dell'angolo corrispondente. Il cerchio trigonometrico definisce tutte le funzioni trigonometriche sulla variabile di arco x. È anche utilizzato come prova, nel risolvere semplici equazioni o disequazioni trigonometriche.
- Esempi di equazioni trigonometriche:
- sin x + sin 2x = 1/2 ; tan x + cot x = 1,732
- cos 3x + sin 2x = cos x ; 2sin 2x + cos x = 1
- Il cerchio trigonometrico unitario.
- È un cerchio con raggio = 1 unità, avente O come origine. Il cerchio trigonometrico unitario definisce 4 funzioni trigonometriche principali della variabile arco x che ruota in senso antiorario su di esso.
- Quando l'arco, con valore x, varia sul cerchio trigonometrico unitario:
- L'asse orizzontale OAx definisce la funzione trigonometrica f(x) = cos x.
- L'asse verticale OBy definisce la funzione trigonometrica f(x) = sin x.
- L'asse verticale AT definisce la funzione trigonometrica f(x) = tan x.
- L'asse orizzontale BU definisce la funzione trigonometrica f(x) = cot x.
- Il cerchio trigonometrico unitario è anche utilizzato per risolvere equazioni e disequazioni trigonometriche di base considerando le varie posizioni dell'arco x su di esso.
Passaggi
-
1Conoscere il concetto di risoluzione.
- Per risolvere un'equazione trigonometrica, trasformala in una delle equazioni trigonometriche di base. Risolvere un'equazione trigonometrica alla fine consiste nel risolvere 4 tipi di equazioni trigonometriche di base.
-
2Capire come risolvere le equazioni di base.
- Ci sono 4 tipi di equazioni trigonometriche di base:
- sin x = a ; cos x = a
- tan x = a ; cot x = a
- Risolvere le equazioni trigonometriche di base consiste nel studiare le diverse posizioni dell'arco x sul cerchio trigonometrico, e utilizzare le tavole di conversione (o la calcolatrice). Per capire in modo completo come risolvere queste equazioni di base, e simili, fai riferimento al libro: "Trigonometry: Solving trig equations and inequalities" (Amazon E-book 2010).
- Esempio 1. Risolvere sin x = 0,866. La tavola di conversione (o calcolatrice) restituisce la soluzione: x = π/3. Il cerchio trigonometrico ha un altro arco (2π/3) che ha lo stesso valore per il seno (0,866). Il cerchio trigonometrico fornisce un'infinità di altre soluzioni che sono dette soluzioni estese.
- x1 = π/3 + 2k.Pi, e x2 = 2π/3. (Soluzioni con periodo (0, 2π))
- x1 = π/3 + 2k Pi, e x2 = 2π/3 + 2k π. (Soluzioni estese).
- Esempio 2. Risolvere: cos x = -1/2. La calcolatrice ritorna x = 2 π/3. Il cerchio trigonometrico fornisce un altro arco x = -2π/3.
- x1 = 2π/3 + 2k.Pi, e x2 = - 2π/3. (Soluzioni con periodo (0, 2π)
- x1 = 2π/3 + 2k Pi, e x2 = -2π/3 + 2k.π. (Soluzioni estese)
- Esempio 3. Risolvere: tan (x - π/4) = 0.
- x = π/4 ; (Soluzioni con periodo π)
- x = π/4 + k Pi; (Soluzioni estese)
- Esempio 4. Risolvere: cot 2x = 1,732. La calcolatrice e il cerchio trigonometrico restituisce:
- x = π/12 ; (Soluzioni con periodo π)
- x = π/12 + k π ; (Soluzioni estese)
-
3Imparare le trasformazioni da utilizzare per semplificare le equazioni trigonometriche.
- Per trasformare una data equazione trigonometrica in una di base, si usano delle trasformazioni algebriche comuni (fattorizzazione, fattori comuni, identità polinomiali,e così via), delle definizioni e proprietà delle funzioni trigonometriche, e delle identità trigonometriche. Ce ne sono circa 31, fra cui le ultime 14 trigonometriche, da 19 a 31, sono dette Identità di Trasformazione, dato che sono utilizzate per trasformare le equazioni trigonometriche. Vedi il libro indicato sopra.
- Esempio 5: L'equazione trigonometrica: sin x + sin 2x + sin 3x = 0 può essere trasformata, usando le identità trigonometriche, in un prodotto di equazioni trigonometriche di base: 4cos x*sin (3x/2)*cos (x/2) = 0. Le equazioni trigonometriche di base che dovranno essere risolte sono: cos x = 0 ; sin (3x/2) = 0 ; e cos (x/2) = 0.
-
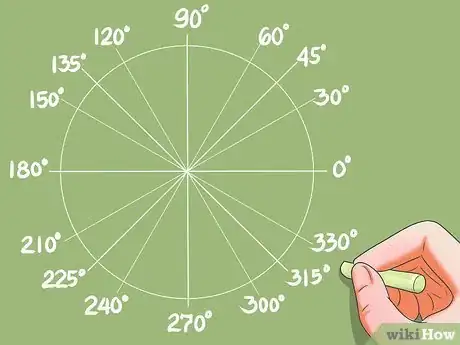
4Trovare gli archi corrispondenti alle funzioni trigonometriche note.
- Prima di imparare a risolvere le equazioni trigonometriche, devi sapere come trovare in modo rapido gli archi delle funzioni trigonometriche note. I valori di conversione per archi (o angoli) sono forniti dalle tavole trigonometriche o da calcolatrici.
- Esempio: Dopo aver risolto, si ottiene cos x = 0,732. La calcolatrice ci fornisce la soluzione arco x = 42.95 gradi. Il cerchio trigonometrico unitario fornirà un'altra soluzione: l'arco che ha lo stesso valore del coseno.
-
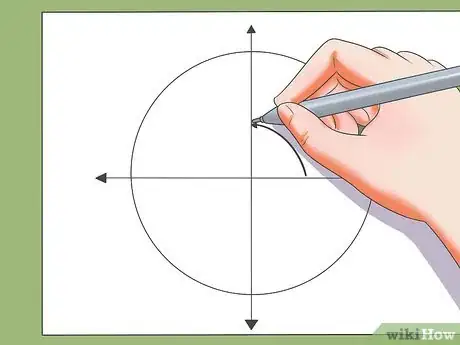
5Disegnare gli archi che sono soluzione sul cerchio trigonometrico.
- Puoi disegnare gli archi sul cerchio trigonometrico per illustrare la soluzione. I punti estremi di questi archi soluzione costituiscono poligoni regolari sul cerchio trigonometrico. Ad esempio:
- I punti estremi della soluzione arco x = π/3 + k.π/2 costituiscono un quadrato sul cerchio trigonometrico.
- Gli archi soluzione x = π/4 + k.π/3 sono rappresentati dai vertici di un esagono regolare sul cerchio trigonometrico unitario.
-
6Imparare gli approcci per risolvere le equazioni trigonometriche.
- Se l'equazione trigonometrica data contiene solo una funzione trigonometrica, risolvila come un'equazione trigonometrica di base. Se l'equazione data contiene due o più funzioni trigonometriche ci sono 2 modi per risolverla, a seconda delle trasformazioni disponibili.
- A. Approccio 1.
- Trasforma l'equazione data in un prodotto della forma: f(x).g(x) = 0 or f(x).g(x).h(x) = 0, in cui f(x), g(x) e h(x) sono funzioni trigonometriche di base.
- Esempio 6. Risolvere: 2cos x + sin 2x = 0 (0 < x < 2π)
- Soluzione. Rimpiazza sin 2x utilizzando l'identità: sin 2x = 2*sin x*cos x.
- cos x + 2*sin x*cos x = 2cos x*( sin x + 1) = 0. Poi, risolvi le 2 funzioni trigonometriche di base: cos x = 0, e (sin x + 1) = 0.
- Esempio 7. Risolvere: cos x + cos 2x + cos 3x = 0. (0 < x < 2π)
- Soluzioni: Trasformalo in un prodotto, utilizzando le identità trigonometriche: cos 2x(2cos x + 1 ) = 0. Poi, risolvi le due equazioni trigonometriche di base: cos 2x = 0, and (2cos x + 1) = 0.
- Esempio 8. Risolvere: sin x - sin 3x = cos 2x. (0 < x < 2π)
- Soluzione. Trasformala in un prodotto, utilizzando le identità: -cos 2x*(2sin x + 1) = 0. Poi risolvi le 2 equazioni trigonometriche di base: cos 2x = 0, and (2sin x + 1) = 0.
- B. Approccio 2.
- Trasforma l'equazione trigonometrica di base in un'equazione trigonometrica avente una sola funzione trigonometrica con variabile. Ci sono due consigli su come selezionare la variabile appropriata. Le variabili comuni da selezionare sono : sin x = t; cos x = t; cos 2x = t, tan x = t e tan (x/2) = t.
- Esempio 9. Risolvere: 3sin^2 x - 2cos^2 x = 4sin x + 7 (0 < x < 2Pi).
- Soluzione. Rimpiazza l'equazione (cos^2 x) by (1 - sin^2 x), poi semplifica l'equazione:
- sin^2 x - 2 - 2sin^2 x - 4sin x - 7 = 0. Sostituisci sin x = t. L'equazione diventa: 5t^2 - 4t - 9 = 0. E' un'equazione quadratica che possiede 2 radici reali: t1 = -1 e t2 = 9/5. La seconda t2 è da scartare siccome > 1. Poi, risolvi: t = sin = -1 --> x = 3π/2.
- Esempio 10. Risolvere: tan x + 2 tan^2 x = cot x + 2.
- Soluzione. Sostituisci tan x = t. Trasforma l'equazione data in un'equazione con variabile t: (2t + 1)(t^2 - 1) = 0. Risolvila per t da questo prodotto, poi risolvi le equazioni trigonometriche di base tan x = t per x.
- Se l'equazione trigonometrica data contiene solo una funzione trigonometrica, risolvila come un'equazione trigonometrica di base. Se l'equazione data contiene due o più funzioni trigonometriche ci sono 2 modi per risolverla, a seconda delle trasformazioni disponibili.
-
7Risolvere tipi particolari di equazioni trigonometriche.
- Ci sono alcuni tipi particolari di equazioni trigonometriche che richiedono delle trasformazioni specifiche. Esempi:
- a*sin x+ b*cos x = c ; a(sin x + cos x) + b*cos x*sin x = c ;
- a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0
-
8Imparare le proprietà periodiche delle funzioni trigonometriche.
- Tutte le funzioni trigonometriche sono periodiche, ovvero tornano allo stesso valore dopo una rotazione di un periodo. Esempi:
- La funzione f(x) = sin x ha 2π come periodo.
- La funzione f(x) = tan x ha π come periodo.
- La funzione f(x) = sin 2x ha π come periodo.
- La funzione f(x) = cos (x/2) ha 4π come periodo.
- Se il periodo è specificato nel problema/test, devi solamente trovare la soluzione arc(s) x all'interno del periodo.
- NOTA: Risolvere un'equazione trigonometrica è un compito difficile che spesso porta ad errori e sbagli. Quindi, le risposte devono essere controllate con attenzione. Dopo averla risolta, puoi controllare le soluzioni utilizzando un grafico o un a calcolatrice per disegnare direttamente la funzione trigonometrica R(x) = 0. Le risposte (radici reali) saranno date in decimali. Ad esempio, π è dato dal valore 3,14.
Pubblicità - Tutte le funzioni trigonometriche sono periodiche, ovvero tornano allo stesso valore dopo una rotazione di un periodo. Esempi:
Informazioni su questo wikiHow
Pubblicità
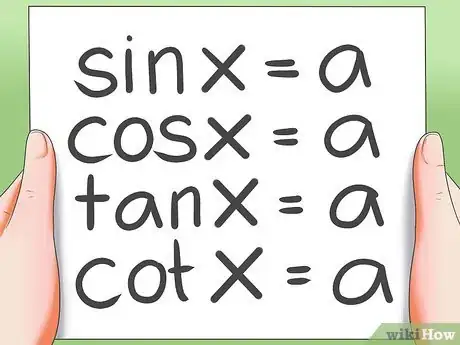

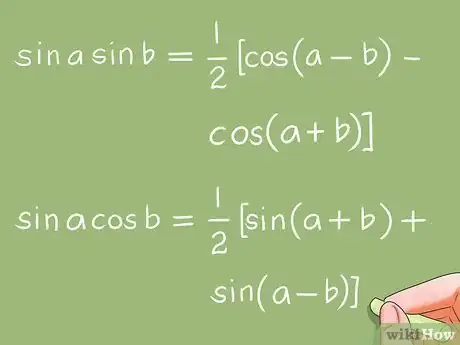
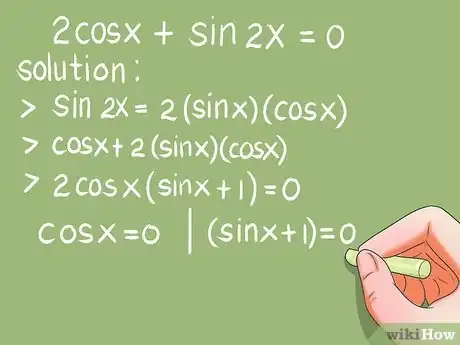
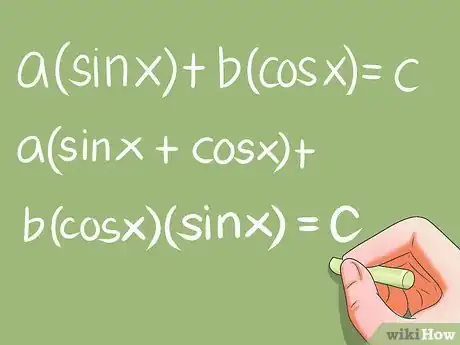
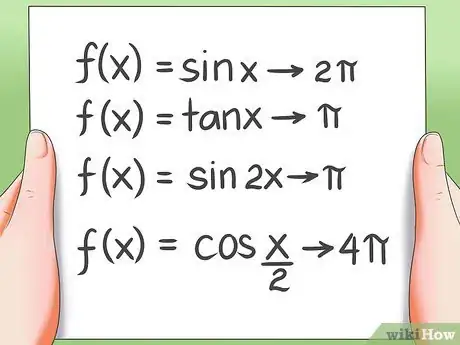




-to-Grams-(g)-Step-12-Version-4.webp)













