Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Ci sono 8 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 22 730 volte
Un polinomio è un'espressione matematica composta da termini che si sommano o si sottraggono fra loro; un termine può essere costituito da costanti, coefficienti e variabili. Quando risolvi un polinomio devi in genere trovare il valore per cui x=0. Quelli di grado inferiore hanno una o due soluzioni, in base al fatto se sono lineari o di secondo grado. Questo genere di polinomi si risolve facilmente sfruttando i concetti algebrici elementari e con i metodi di scomposizione in fattori. Per imparare a risolvere quelli di grado superiore puoi leggere questo articolo.
Passaggi
Polinomi di Primo Grado
-
1Determina se si stratta di un polinomio lineare. Con questo termine si indica un'espressione di primo grado.[1] Questo significa che non ci sono variabili con esponente (o meglio con un esponente maggiore di 1); dato che si tratta di un'espressione di primo grado, prevede una sola soluzione, o radice.[2]
- Per esempio, è un polinomio di primo grado perché la variabile ha esponente uguale a 1.
-
2Imposta l'equazione uguale a zero. Questo passaggio è necessario per risolvere tutti i polinomi.
- Per esempio, .
-
3Isola il termine della variabile. Somma o sottrai la costante a entrambi i lati dell'equazione; la costante è il parametro senza variabile.[3]
- Per esempio, per isolare nell'equazione , dovresti sottrarre da entrambi i lati:
.
- Per esempio, per isolare nell'equazione , dovresti sottrarre da entrambi i lati:
-
4Risolvi per la variabile. In genere, devi dividere entrambi i termini dell'equazione per il coefficiente della variabile; in questo modo ottieni la radice, o soluzione, del polinomio.
- Per esempio, per trovare il valore di in , dovresti dividere entrambi i termini per :
di conseguenza, la soluzione di è .
Pubblicità - Per esempio, per trovare il valore di in , dovresti dividere entrambi i termini per :
Polinomi di Secondo Grado
-
1Determina se hai un polinomio di secondo grado. A volte, si definisce anche polinomio quadratico;[4] questo significa che non c'è alcuna variabile con un esponente maggiore di 2. Dato che si tratta di un polinomio di secondo grado, prevede due radici, o soluzioni.[5]
- Per esempio, è un polinomio di secondo grado perché la variabile ha un esponente pari a .
-
2Assicurati che sia scritto in ordine di grado. Questo significa che il termine con esponente uguale a deve essere il primo a sinistra, seguito da quello di primo grado e infine dalla costante.[6]
- Per esempio, dovresti riscrivere in questa forma: .
-
3Imposta un'equazione pari a zero. Questo passaggio è necessario per risolvere tutti i polinomi.
- Per esempio: .
-
4Riscrivi l'equazione come un'espressione in quattro termini. Per procedere devi separare il termine di primo grado (il termine ); devi trovare due numeri la cui somma sia pari al coefficiente della variabile e il prodotto pari alla costante.[7]
- Per esempio, se consideri il polinomio di secondo grado , devi trovare i due numeri ( e ) per cui , e .
- Dato che la costante è negativa (), sai che uno dei due numeri è minore di zero.
- Dovresti renderti conto che e . Di conseguenza, puoi riscrivere come ; pertanto, l'equazione si presenta in questo modo: .
-
5Raccogli in fattori. Estrai quello comune per i primi due termini del polinomio.[8]
- Nell'esempio considerato finora, , i primi due termini sono . Il fattore comune è , quindi puoi riscriverli come .
-
6Raccogli in fattori il secondo gruppo. Estrai il fattore comune degli altri due termini del polinomio.
- Per esempio, osservando , i due termini successivi sono il cui fattore comune è , ottenendo di conseguenza .
-
7Riscrivi il polinomio come due binomi. Un binomio è un'espressione composta da due termini. Uno è già presente ed è rappresentato dalle espressioni raccolte fra parentesi e che sono uguali fra loro; l'altro è la combinazione dei fattori comuni che si trovano fuori dalle parentesi, ma che possono essere combinati per la proprietà distributiva.
- Per esempio, dopo aver raccolto i fattori comuni, l'equazione diventa .
- Il primo binomio è .
- Il secondo è .
- Di conseguenza il polinomio iniziale di secondo grado, , può essere riscritto come: .
-
8Trova la prima soluzione, o radice. Per farlo, devi risolvere il primo binomio per .[9]
- Nell'esempio considerato, per calcolare la prima radice di , devi imporre il primo binomio uguale a e trovare . Quindi:
La prima soluzione del polinomio di secondo grado è .
- Nell'esempio considerato, per calcolare la prima radice di , devi imporre il primo binomio uguale a e trovare . Quindi:
-
9Trova la seconda radice, o soluzione. In tal caso, devi risolvere il secondo binomio per .[10]
- Per esempio, per calcolare la seconda radice di devi imporre il secondo binomio pari a e svolgere le operazioni per trovare . Quindi:
La seconda radice del polinomio di secondo grado è .
Pubblicità - Per esempio, per calcolare la seconda radice di devi imporre il secondo binomio pari a e svolgere le operazioni per trovare . Quindi:
Consigli
- Non spaventarti se ci sono variabili diverse, per esempio "t", o se ti imbatti in un'equazione posta uguale a f(x) invece che a 0. Se l'enunciato del problema richiede delle radici, dei fattori o degli zeri, trattalo semplicemente come qualsiasi altro esercizio.
- Ricorda l'ordine delle operazioni; svolgi prima quelle tra parentesi, poi le moltiplicazioni e le divisioni e infine le somme e le sottrazioni.[11]
Riferimenti
- ↑ http://www.mathwords.com/l/linear_polynomial.htm
- ↑ https://www.math.utah.edu/~wortman/1050-text-calp.pdf
- ↑ http://www.mathwords.com/c/constant.htm
- ↑ http://www.mathwords.com/q/quadratic_polynomial.htm
- ↑ http://www.themathpage.com/aprecalc/quadratic-equation.htm#double
- ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/trinomials/a_is_not_1/trinomials_a_is_not_1.html
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
- ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/trinomials/a_is_not_1/trinomials_a_is_not_1.html
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
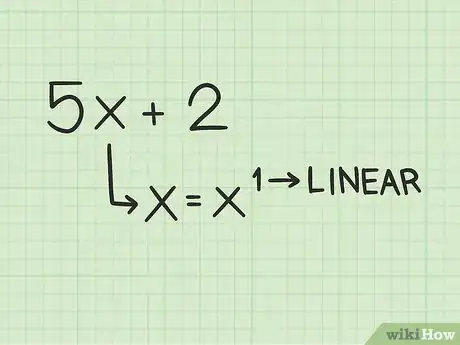


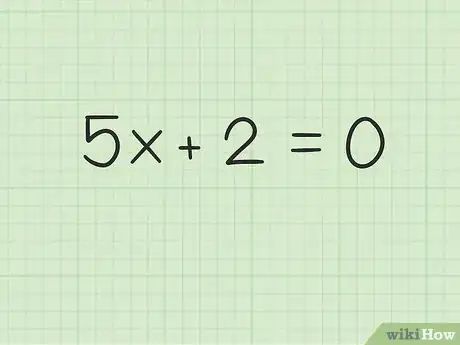

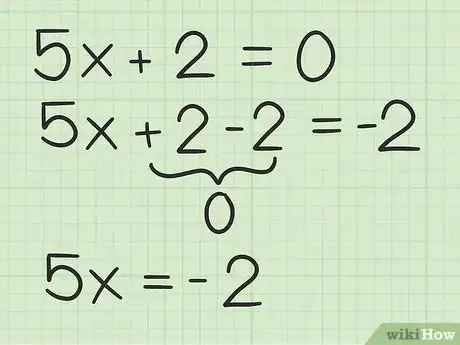



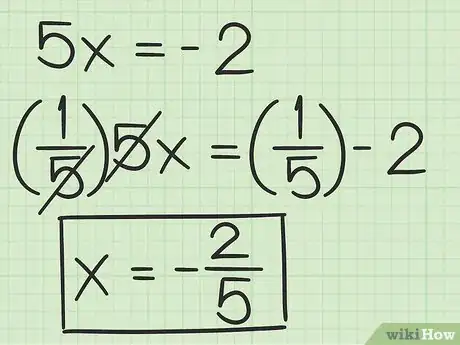



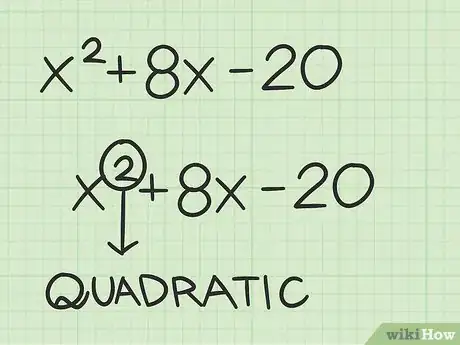

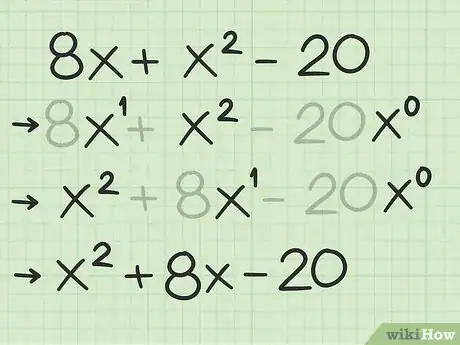

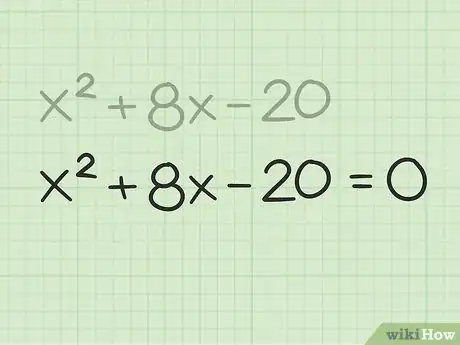

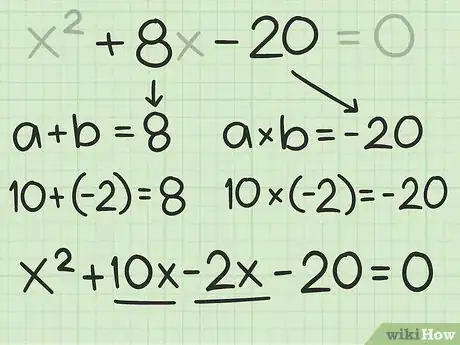










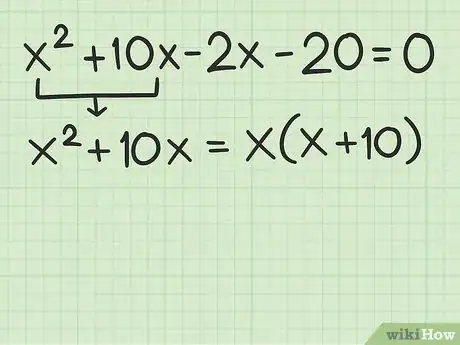


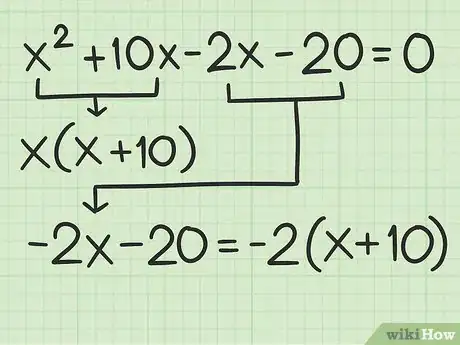



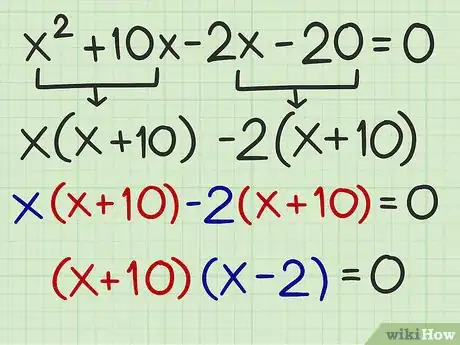




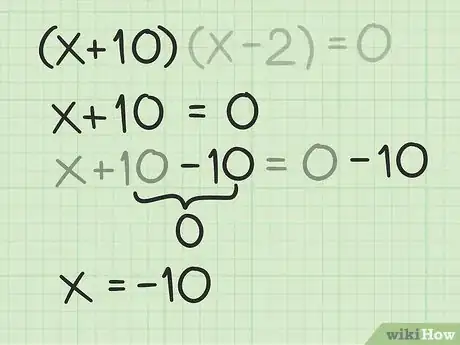





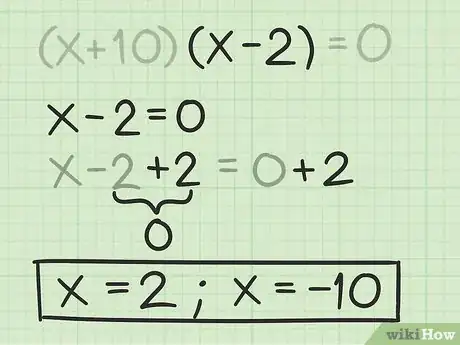







-to-Grams-(g)-Step-12-Version-4.webp)














