X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 8 400 volte
Le equazioni lineari a più incognite sono equazioni con due o più variabili (generalmente rappresentate da 'x' e 'y'). Ci sono vari modi per risolvere tali equazioni, incluse l'eliminazione e la sostituzione.
Passaggi
Metodo 1
Metodo 1 di 3:
Comprendere le Componenti delle Equazioni Lineari
-
1Che cosa sono le equazioni a più incognite? Due o più equazioni lineari raggruppate insieme sono dette sistema. Ciò significa che un sistema di equazioni lineari si ha quando due o più equazioni lineari vengono risolte contemporaneamente.[1] Ad esempio:
- 8x - 3y = -3
- 5x - 2y = -1
- Queste sono due equazioni lineari che devi risolvere contemporaneamente, ovvero devi usare entrambe le equazioni per la risoluzione.
-
2Devi trovare i valori delle variabili, o incognite. La soluzione di un problema con equazioni lineari è una coppia di numeri che rende vere entrambe le equazioni.
- Nel nostro esempio, stai cercando di trovare i valori numerici di ‘x’ e ‘y’ che rendono vere entrambe le equazioni. Nell'esempio, x = -3 e y = -7. Inseriscili nell'equazione. 8(-3) - 3(-7) = -3. È VERO. 5(-3) -2(-7) = -1. Anche questo è VERO.
-
3Che cos'è un coefficiente numerico? Il coefficiente numerico è semplicemente un numero che precede una variabile.[2] Userai i coefficienti numerici se scegli di utilizzare il metodo dell'eliminazione. Nel nostro esempio, i coefficienti numerici sono:
- 8 e 3 nella prima equazione; 5 e 2 nella seconda equazione.
-
4Impara la differenza fra la risoluzione attraverso l'eliminazione e quella attraverso la sostituzione. Quando utilizzi il metodo dell'eliminazione per risolvere un'equazione lineare a più incognite, ti liberi di una delle variabili con cui stai lavorando (ad esempio ‘x’) in modo da poter trovare il valore dell'altra variabile (‘y’). Quando trovi il valore di ‘y’, lo inserisci nell'equazione per trovare quello di ‘x’ (non preoccuparti: lo vedremo dettagliatamente nel Metodo 2).
- Invece, utilizzi il metodo della sostituzione quando inizi a risolvere una sola equazione in modo da poter trovare il valore di una delle incognite. Dopo averla risolta, inserirai il risultato nell'altra equazione, creando di fatto un'equazione più lunga invece di averne due più piccole. Nuovamente, non preoccuparti: lo vedremo dettagliatamente nel Metodo 3.
-
5Ci possono essere equazioni lineari a tre o più incognite. Si può risolvere un'equazione a tre incognite nello stesso modo in cui si risolvono quelle a due incognite. Puoi usare sia l'eliminazione sia la sostituzione; ci vorrà un po' più di lavoro per trovare le soluzioni, ma il procedimento è lo stesso.Pubblicità
Metodo 2
Metodo 2 di 3:
Risolvere un'Equazione Lineare con l'Eliminazione
-
1Osserva le equazioni. Per poterle risolvere, devi imparare a riconoscere le componenti dell'equazione. Usiamo questo esempio per imparare come eliminare le incognite:
- 8x - 3y = -3
- 5x - 2y = -1
-
2Scegli una variabile da eliminare. Per eliminare una variabile, il suo coefficiente numerico (il numero che precede la variabile) deve essere opposto rispetto all'altra equazione (ad esempio 5 e -5 sono opposti). Lo scopo è liberarsi di un'incognita, in modo da poter trovare il valore dell'altra eliminandone una attraverso la sottrazione. Ciò significa fare in modo che i coefficienti della stessa incognita in entrambe le equazioni si annullino l'uno con l'altro.[3] Ad esempio:
- In 8x - 3y = -3 (equazione A) e 5x - 2y = -1 (equazione B), puoi moltiplicare l'equazione A per 2 e l'equazione B per 3, in modo da ottenere 6y nell'equazione A e 6y nell'equazione B.
- Equazione A: 2(8x - 3y =-3) = 16x -6y = -6.
- Equazione B: 3(5x - 2y = -1) = 15x -6y =-3
-
3Somma o sottrai le due equazioni per eliminare una delle incognite e risolvila per trovare il valore dell'altra. Ora che una delle incognite può essere eliminata, puoi farlo utilizzando l'addizione o la sottrazione. Quale utilizzare dipenderà da quella che serve a eliminare l'incognita. Nel nostro esempio, useremo la sottrazione, perché abbiamo 6y in entrambe le equazioni:
- (16x - 6y = -6) - (15x - 6y = -3) = 1x = -3. Quindi x = -3.
- In altri casi, se il coefficiente numerico di x non è 1 dopo aver eseguito l'addizione o la sottrazione, dovremo dividere entrambi i lati dell'equazione per il coefficiente stesso per semplificare l'equazione.
-
4Inserisci il valore ottenuto per trovare il valore dell'altra incognita. Ora che hai trovato il valore di ‘x’, puoi inserirlo nell'equazione originale per trovare il valore di ‘y’.[4] Quando vedi che funziona in una delle equazioni, puoi provare a inserirlo anche nell'altra per controllare la correttezza del risultato:
- Equazione B: 5(-3) - 2y = -1 quindi -15 -2y = -1. Somma 15 a entrambi i lati e ottieni -2y = 14. Dividi entrambi i lati per -2 e ottieni y = -7.
- Quindi x = -3 e y = -7.
-
5Inserisci i valori ottenuti in entrambe le equazioni per accertarti che siano corretti. Quando hai trovato i valori delle incognite, inseriscili nelle equazioni originali per accertarti che siano corretti. Se una delle equazioni non risulta vera con i valori che hai trovato, dovrai riprovare da capo.
- 8(-3) - 3(-7) = -3 quindi -24 +21 = -3 VERO.
- 5(-3) -2(-7) = -1 quindi -15 + 14 = -1 VERO.
- Quindi, i valori che hai ottenuto sono corretti.
Pubblicità
Metodo 3
Metodo 3 di 3:
Risolvere un'Equazione Lineare con la Sostituzione
-
1Inizia risolvendo una delle equazioni per una delle variabili. Non importa da quale equazione decidi di iniziare, né quale variabile scegli di trovare per prima: in ogni caso, otterrai le stesse soluzioni. Tuttavia, è meglio rendere il processo più semplice possibile. Dovresti iniziare dall'equazione che ti sembra più semplice da risolvere.[5] Quindi, se c'è un'equazione con un coefficiente di valore 1, come x - 3y = 7, potresti partire da questa, perché sarà più semplice trovare ‘x’. Ad esempio, le nostre equazioni sono:
- x - 2y = 10 (equazione A) e -3x -4y = 10 (equazione B). Potresti iniziare a risolvere x - 2y = 10 poiché il coefficiente di x in questa equazione è 1.
- Risolvere per x l'equazione A significherebbe sommare 2y a entrambi i lati. Quindi x = 10 + 2y.
-
2Sostituisci ciò che hai ottenuto nel passaggio 1 nell'altra equazione. In questo passaggio, devi inserire (o sostituire) la soluzione trovata per ‘x’ nell'equazione che non hai utilizzato. Ciò ti permetterà di trovare l'altra incognita, in questo caso ‘y’.[6] Provaci:
- Inserisci la ‘x’ dell'equazione B nell'equazione A: -3(10 + 2y) -4y = 10. Come puoi vedere, abbiamo eliminato ‘x’ dall'equazione e inserito ciò a cui ‘x’ è uguale.
-
3Trova il valore dell'altra incognita. Ora che hai eliminato una delle incognite dall'equazione, puoi trovare il valore dell'altra. Si tratta semplicemente di risolvere una normale equazione lineare a una incognita. Risolviamo quella del nostro esempio:
- -3(10 + 2y) -4y = 10 so -30 -6y -4y = 10.
- Somma le y: -30 - 10y = 10.
- Sposta -30 dall'altro lato (cambiando il segno): -10y = 40.
- Risolvi per trovare y: y = -4.
-
4Trova la seconda incognita. Per farlo, inserisci il valore di ‘y’ (o della prima incognita) che hai trovato in una delle equazioni originali. Poi risolvila per trovare il valore dell'altra incognita, in questo caso ‘x’. Proviamo:
- Trova ‘x’ nell'equazione A inserendo y = -4: x - 2(-4) = 10.
- Semplifica l'equazione: x + 8 = 10.
- Risolvi per trovare x: x = 2.
-
5Controlla che i valori che hai trovato funzionino in tutte le equazioni. Inserisci entrambi i valori in ogni equazione per accertarti di ottenere equazioni vere. Vediamo se i nostri valori funzionano:
- L'equazione A: 2 - 2(-4) = 10 è VERA.
- L'equazione B: -3(2) -4(-4) = 10 è VERA.
Pubblicità
Consigli
- Fai attenzione ai segni; poiché si utilizzano molte operazioni di base, il cambiamento dei segni può modificare ogni passaggio dei calcoli.
- Controlla i risultati finali. Puoi farlo sostituendo i valori ottenuti alle variabili corrispondenti in tutte le equazioni originali; se i risultati di entrambi i lati dell'equazione coincidono, i risultati che hai trovato sono esatti.
Pubblicità
Riferimenti
- ↑ Steward, J., Lothar, R., Watson, S., Algebra and Trigonometry. Second Edition. Singapore: Thomson Learning Asia,
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut49_systwo.htm
- ↑ Steward, J., Lothar, R., Watson, S., Algebra and Trigonometry. Second Edition. Singapore: Thomson Learning Asia,
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut49_systwo.htm
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut49_systwo.htm
- ↑ Steward, J., Lothar, R., Watson, S., Algebra and Trigonometry. Second Edition. Singapore: Thomson Learning Asia,
Informazioni su questo wikiHow
Pubblicità
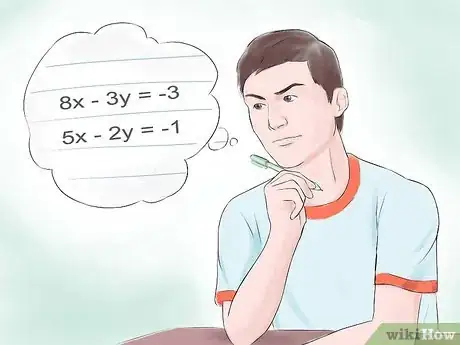
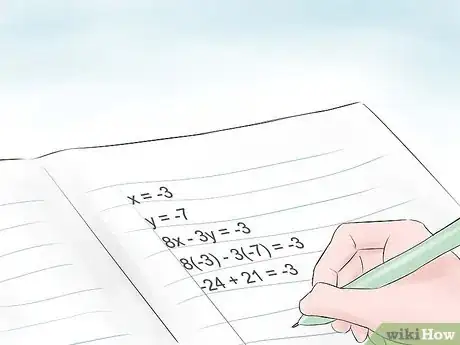
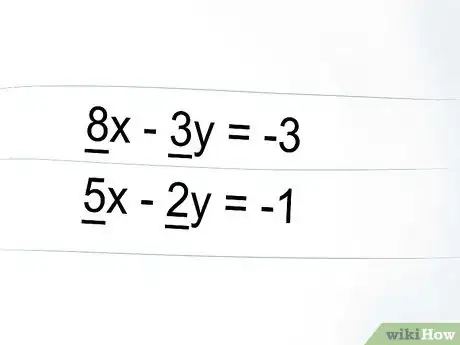

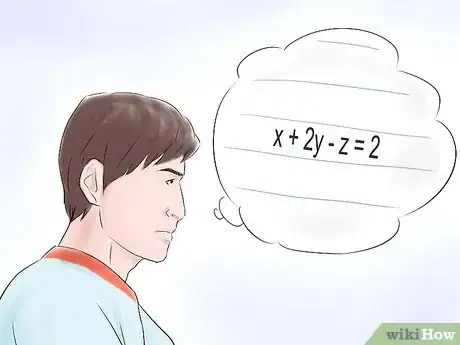
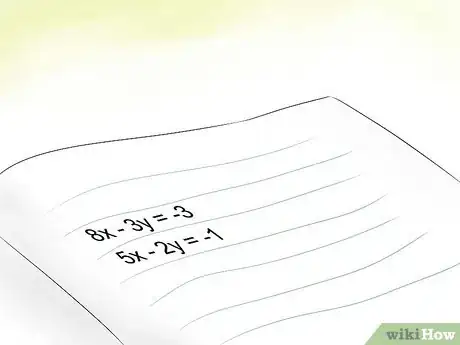


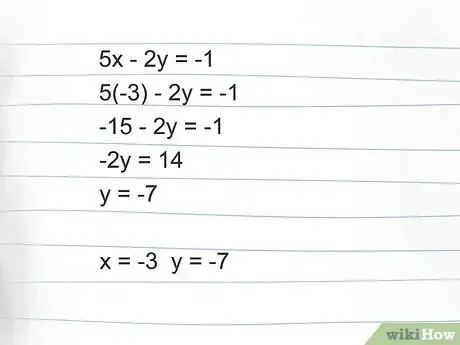
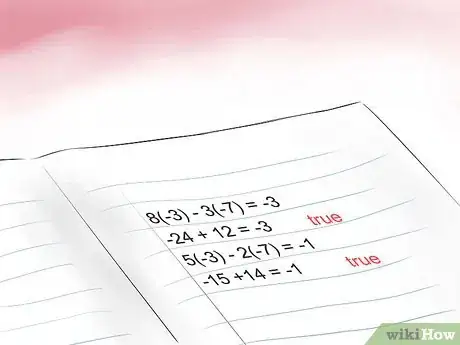
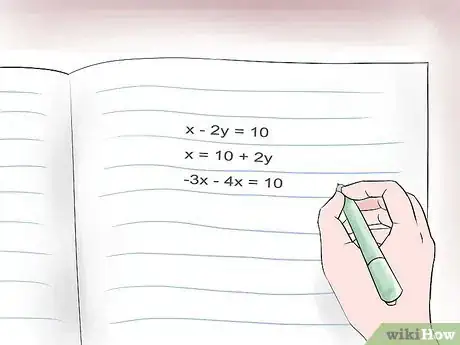
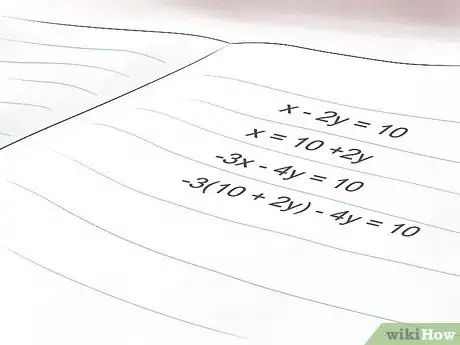
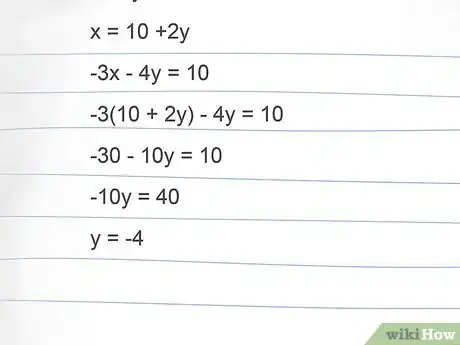
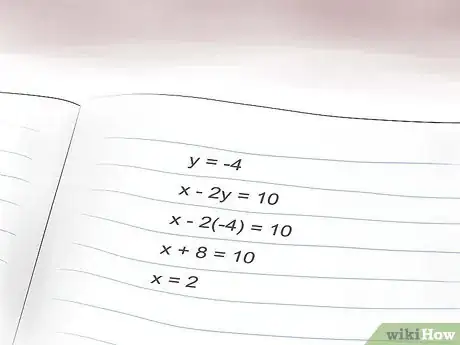
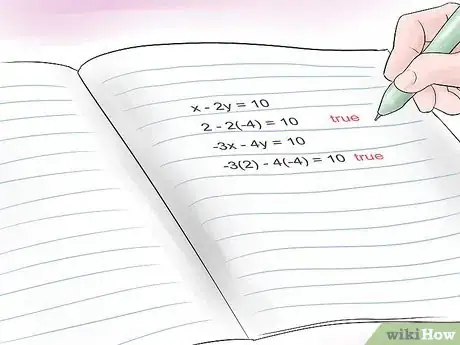



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
