wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 25 256 volte
Se l'intimidatorio simbolo della radice quadrata può far venire la nausea a molti studenti, le operazioni con le radici quadrate non sono così difficili da risolvere come possono sembrare a prima vista. Le operazioni con le radici quadrate semplici possono spesso essere risolte facilmente esattamente come le moltiplicazioni e le divisioni di base. Radici quadrate più complesse, invece, possono richiedere un po' più di lavoro, ma con il metodo giusto anch'esse possono diventare facili da estrarre. Comincia oggi stesso a fare pratica con le radici quadrate per imparare questa nuova capacità matematica radicale!
Passaggi
Comprendere i Quadrati e le Radici Quadrate
-
1Il quadrato di un numero è il risultato della sua moltiplicazione per se stesso. Per comprendere le radici quadrate, di solito è meglio cominciare dai quadrati. I quadrati sono semplici da comprendere: elevare un numero al quadrato significa solamente moltiplicarlo per se stesso. Per esempio, 3 al quadrato è lo stesso che 3 × 3 = 9, mentre 9 al quadrato è uguale a 9 × 9 = 81. I quadrati vengono scritti indicando un piccolo "2" in alto a destra del numero moltiplicato, in questo modo: 32, 92, 1002, e così via.
- Prova a elevare al quadrato qualche altro numero per conto tuo per capire se hai assimilato al meglio il concetto. Ricorda, elevare un numero al quadrato significa semplicemente moltiplicarlo per se stesso. Lo puoi fare anche con i numeri negativi, il risultato sarà sempre positivo. Ad esempio: -82 = -8 × -8 = 64.
-
2Per le radici quadrate, trova l'"inverso" di un quadrato. Il simbolo della radice quadrata (&# 8730;, chiamato anche "radicale") rappresenta sostanzialmente l'operazione "opposta" a quella del simbolo 2 . Quando vedi un radicale, dovrai chiederti: "che numero si può moltiplicare per se stesso per dare come risultato il numero presente sotto la radice?" Per esempio, se vedi √(9), dovrai trovare il numero che può essere elevato al quadrato per ottenere 9. In questo caso, la risposta è tre, perché 32 = 9.
- Come esempio ulteriore, proviamo a trovare la radice quadrata di 25 (√(25)), ossia il numero che elevato al quadrato dia 25. Siccome 52 = 5 × 5 = 25, possiamo dire che √(25) = 5.
- Puoi pensare questo procedimento anche come il "disfare" un quadrato. Per esempio, se vuoi trovare √(64), la radice quadrata di 64, comincia a pensare 64 come 82. Siccome il simbolo di una radice quadrata, in sostanza, "elimina" quello di un quadrato, possiamo dire che √(64) = √(82) = 8.
-
3Conosci la differenza tra quadrati perfetti e imperfetti. Fino ad ora, le soluzioni alle nostre operazioni con le radici quadrate sono state dei bei numeri interi puliti. Non è sempre così, infatti le radici quadrate alle volte possono avere soluzioni costituite da decimali parecchio lunghi e scomodi. I numeri le cui radici quadrate sono numeri interi (in altre parole, senza frazioni né decimali) vengono detti quadrati perfetti. Tutti gli esempi elencati sopra (9, 25 e 64) sono quadrati perfetti perché quando estrai le loro radici quadrate, ottieni dei numeri interi (3, 5 e 8).
- Al contrario, i numeri che una volta estratta la radice quadrata non diano come risultato dei numeri interi, vengono detti quadrati imperfetti. Estraendo la radice quadrata di uno di questi numeri, si ottiene di solito una frazione o un numero decimale. Talvolta, i decimali in questione possono essere alquanto complicati. Per esempio √(13) = 3,605551275464...
-
4Memorizza i primi 10-12 quadrati perfetti. Come avrai probabilmente notato, estrarre la radice quadrata dei quadrati perfetti può essere abbastanza facile! Dato che la risoluzione di questi problemi è molto semplice, vale la pena impiegare del tempo per memorizzare le radici quadrate della prima decina di quadrati perfetti. Avrai parecchio a che fare con questi numeri, quindi prendendoti il tempo di impararli a memoria potrai risparmiarne parecchio più avanti. I primi 12 quadrati perfetti sono:
- 12 = 1 × 1 = 1
- 22 = 2 × 2 = 4
- 32 = 3 × 3 = 9
- 42 = 4 × 4 = 16
- 52 = 5 × 5 = 25
- 62 = 6 × 6 = 36
- 72 = 7 × 7 = 49
- 82 = 8 × 8 = 64
- 92 = 9 × 9 = 81
- 102 = 10 × 10 = 100
- 112 = 11 × 11 = 121
- 122 = 12 × 12 = 144
-
5Semplifica le radici quadrate rimuovendo i quadrati perfetti, quando possibile. Trovare le radici quadrate dei quadrati imperfetti può essere alle volte abbastanza complicato, specialmente se non stai usando una calcolatrice (nella sezione più in basso troverai degli accorgimenti per rendere il processo più facile). Tuttavia, è spesso possibile semplificare i numeri sotto radice e renderli più semplici per fare i calcoli. Per farlo, devi semplicemente scomporre in fattori il numero sotto radice, estrarre la radice quadrata di ogni fattore che è un quadrato perfetto e scrivere la soluzione fuori dal radicale. È decisamente più facile di quanto sembri: continua a leggere per scoprire di più!
- Mettiamo di voler trovare la radice quadrata di 900. A prima vista sembra piuttosto difficile! Tuttavia, non sarà così complicato se scomponiamo 900 in fattori. I fattori sono i numeri che si possono moltiplicare tra loro per formare un altro numero. Per esempio, siccome puoi ottenere 6 moltiplicando 1 × 6 e 2 × 3, i fattori di 6 sono 1, 2, 3 e 6.
- Invece di fare i calcoli con il numero 900, che è piuttosto complicato, scrivilo come 9 × 100. Ora, siccome 9, che è un quadrato perfetto, è separato da 100, possiamo estrarre la sua radice quadrata singolarmente. √(9 × 100) = √(9) × √(100) = 3 × √(100). In altre parole, √(900) = 3√(100).
- Possiamo quindi semplificarlo ulteriormente scomponendo 100 nei fattori 25 e 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Perciò possiamo dire che √(900) = 3(10) = 30.
-
6Utilizza i numeri immaginari per le radici quadrate dei numeri negativi. Pensaci: quale numero moltiplicato per se stesso dà -16? Né 4 né -4: elevandoli al quadrato si ottiene in entrambi i casi il numero positivo 16. Ti arrendi? In effetti, non esiste un modo per scrivere la radice quadrata di -16 (e di ogni altro numero negativo) con i numeri reali. In questi casi, bisogna far ricorso ai numeri immaginari (di solito nella forma di lettere o simboli) per sostituirli al posto della radice quadrata del numero negativo. Ad esempio, la variabile i viene di solito impiegata per la radice quadrata di -1. Come regola generale, la radice quadrata di un numero negativo sarà (o includerà) sempre un numero immaginario.
- Nota che, sebbene i numeri immaginari non possano venire rappresentati con le cifre classiche, possono comunque essere trattati come i numeri reali sotto molti aspetti. Per esempio, le radici quadrate dei numeri negativi possono venire elevate al quadrato per ottenere quegli stessi numeri negativi, esattamente come ogni altra radice quadrata di un numero positivo. Per esempio, i2 = -1.
Pubblicità
Utilizzare il Metodo della Divisione in Colonna
-
1Disponi la radice quadrata come in una divisione in colonna. Sebbene possa richiedere abbastanza tempo, questo metodo permette di risolvere le radici quadrate di quadrati imperfetti piuttosto difficili senza l'uso della calcolatrice. Per farlo, utilizzeremo un metodo di risoluzione (o algoritmo) che è simile, ma non esattamente identico, alla divisione in colonna di base.
- Comincia scrivendo la radice quadrata nella stessa forma di una divisione in colonna. Per esempio, mettiamo caso di voler trovare la radice quadrata di 6,45, che non è sicuramente un comodo quadrato perfetto. Innanzitutto, scrivi il consueto simbolo della radice (√) e il numero sotto di esso. Poi, fai una linea sotto al numero di modo che si venga a trovare in una sorta di piccola "scatola", come in una divisione in colonna. Una volta finito, dovresti avere un simbolo con una lunga coda "√" e un 6,45 scritto sotto.
- Scrivi i numeri sopra la radice di modo da essere sicuro di lasciare spazio.
-
2Raggruppa le cifre a coppie. Per cominciare a risolvere il problema, raggruppa a coppie le cifre del numero sotto il segno del radicale, partendo dalla virgola decimale. Potrà essere utile fare dei piccoli segni (come punti, barre, virgole, ecc.) tra le varie coppie per tenerne traccia.
- Nel nostro esempio, divideremo 6,45 in questo modo: 6-,45-00. Nota la presenza di una cifra che "avanza" sulla sinistra, va bene così.
-
3Trova il numero più grande il cui quadrato sia minore o uguale al primo "gruppo" di cifre. Comincia dal primo numero, la prima coppia sulla sinistra. Scegli il numero più grande con un quadrato che sia minore o uguale a quel "gruppo" di cifre. Per esempio, se il gruppo di cifre era 37, scegli 6, perché 62 = 36 < 37 ma 72 = 49 > 37. Scrivi questo numero sopra il primo gruppo. È la prima cifra della tua soluzione.
- Nel nostro esempio, il primo gruppo di 6-,45-00 è costituito da 6. Il numero più grande che, elevato al quadrato sia minore o uguale a 6 è 2, dato che 22 = 4. Scriviamo un "2" sopra il 6 presente sotto la radice.
-
4Raddoppia il numero che hai appena scritto, portalo sotto e sottrailo. Prendi la prima cifra della tua soluzione (il numero che hai appena trovato) e raddoppialo. Scrivilo sotto il primo gruppo e sottrailo per trovare la differenza. Porta sotto, accanto al risultato, la coppia di numeri successiva. Infine, scrivi sulla sinistra l'ultima cifra del doppio (della prima cifra) della soluzione e lascia uno spazio a fianco.
- Nel nostro esempio, cominceremo prendendo il doppio di 2, la prima cifra della nostra soluzione. 2 × 2 = 4. Quindi, sottrarremo 4 da 6 (il nostro primo "gruppo"), ottenendo 2 come risultato. In seguito, porteremo sotto il gruppo successivo (45) per ottenere 245. Infine, scriveremo 4 ancora una volta sulla sinistra, lasciando un piccolo spazio su cui scrivere, in questo modo: 4_.
-
5Riempi lo spazio vuoto. In seguito, dovrai aggiungere una cifra sul lato destro del numero che hai appena scritto a sinistra. Scegli la cifra più grande possibile (da moltiplicare per il nuovo numero), ma comunque inferiore o uguale al numero che hai "portato giù". Ad esempio, se il numero che hai "portato giù" è 1700 e il numero sulla sinistra è 40_, dovrai riempire lo spazio vuoto con "4" perché 404 × 4 = 1616 < 1700, mentre 405 × 5 = 2025. Il numero che trovi a questo punto del procedimento, sarà la seconda cifra della tua soluzione, e lo puoi quindi aggiungere sopra il segno della radice.
- Nel nostro esempio, dobbiamo trovare il numero che riempiendo lo spazio vuoto di 4_ × _ dia il risultato maggiore possibile – ma comunque minore o uguale a 245. In questo caso, la risposta sarà 5. 45 × 5 = 225, mentre 46 × 6 = 276.
-
6Continua, utilizzando i numeri "negli spazi vuoti" per il risultato. Continua a eseguire questo metodo di divisione in colonna modificato finché non cominci a ottenere degli zeri sottraendo ai numeri "portati sotto", oppure finché raggiungi il livello di approssimazione richiesta. Quando hai finito, i numeri che hai usato a ogni passaggio per riempire gli spazi bianchi (più il primo numero in assoluto) formeranno le cifre della tuo soluzione.
- Continuando nel nostro esempio, sottraiamo 225 da 245 per ottenere 20. Poi, portiamo sotto la coppia di cifre successiva, 00, per fare 2000. Raddoppiando i numeri sopra il segno della radice, otteniamo 25 × 2 = 50. Risolvendo lo spazio bianco di 50_ × _ =/< 2000, otteniamo 3. A questo punto, avremo "253" sopra il segno della radice. Ripetendo lo stesso procedimento ancora una volta, otterremo 9 come cifra successiva.
-
7Sposta sopra la virgola decimale dal tuo "dividendo" di partenza. Per completare la tua soluzione, dovrai mettere la virgola decimale al posto giusto. Per fortuna, è facile: tutto ciò che dovrai fare sarà farla corrispondere con la virgola decimale del numero di partenza. Per esempio, se il numero sotto il segno della radice è 49,8, dovrai spostare semplicemente la virgola tra i due numeri situati sopra il 9 e l'8.
- Nel nostro esempio, il numero sotto il segno della radice è 6,45, quindi sposteremo semplicemente la virgola sopra mettendola tra le cifre 2 e 5 del nostro risultato, ottenendo 2,539.
Pubblicità
Eseguire Rapidamente una Stima Approssimata dei Quadrati Imperfetti
-
1Trova i quadrati non perfetti facendo delle stime approssimative. Una volta che avrai memorizzato i quadrati perfetti, trovare le radici quadrate dei quadrati imperfetti diventerà molto più facile. Visto che conosci già più di una decina di quadrati perfetti, ogni numero che si trovi tra due di questi, potrà essere trovato "smussando" sempre di più una stima approssimativa presente tra questi valori. Per cominciare, trova i due quadrati perfetti tra i quali è situato il numero. In seguito, determina a quale di questi due numeri si avvicina di più.
- Per esempio, mettiamo di dover trovare la radice quadrata di 40. Visto che abbiamo memorizzato i quadrati perfetti, possiamo dire che 40 è tra 62 e 72, ossia tra 36 e 49. Siccome 40 è maggiore di 62, la sua radice quadrata sarà maggiore di 6; e siccome è minore di 72, anche la sua radice quadrata sarà minore di 7. Inoltre, 40 è un po' più vicino a 36 che a 49, quindi il risultato sarà probabilmente più prossimo a 6 che a 7. Nei passaggi successivi, affineremo ulteriormente la precisione della nostra soluzione.
-
2Approssima la radice quadrata a una cifra decimale. Una volta che hai trovato due quadrati perfetti tra i quali si situa il numero, diventerà una semplice questione di aumentare la tua approssimazione finché non raggiungi una soluzione che ti soddisfi; più ti spingerai nel dettaglio, più accurata sarà la soluzione. Per cominciare, scegli una cifra decimale "del valore dei decimi" per la soluzione, non dovrà essere per forza esatta, ma ti risparmierà parecchio tempo utilizzare il buon senso per scegliere quella che più si avvicina al risultato giusto.
- Nel nostro problema di esempio, un'approssimazione ragionevole per la radice quadrata di 40 potrebbe essere 6,4, siccome sappiamo, dal procedimento sopra, che la soluzione è probabilmente più vicina a 6 che a 7.
-
3Moltiplica il numero approssimato per se stesso. In seguito, eleva al quadrato la tua stima. A meno che tu non sia davvero fortunato, non otterrai subito il numero di partenza: sarai leggermente al di sopra o al di sotto di esso. Se la tua soluzione è un numero leggermente superiore a quello dato, prova di nuovo con un'approssimazione un poco inferiore (e viceversa se la soluzione è inferiore, prova con una stima maggiore).
- Moltiplica 6,4 per se stesso per ottenere 6,4 × 6,4 = 40,96, che è leggermente maggiore del numero di partenza di cui vogliamo trovare la radice.
- Poi, siccome siamo andati oltre il risultato richiesto, moltiplicheremo per se stesso il numero di un decimo inferiore alla nostra stima in eccesso, ottenendo 6,3 × 6,3 = 39,69, che questa volta è leggermente inferiore al numero di partenza. Questo significa che la radice quadrata di 40 è da qualche parte tra 6,3 e 6,4. Inoltre, siccome 39,69 è più vicino a 40 rispetto a 40,96, sapremo che la radice quadrata sarà più vicina a 6,3 che a 6,4.
-
4Continua il processo di approssimazione quanto richiesto. A questo punto, se sei soddisfatto con le soluzioni trovate, potresti voler semplicemente sceglierne e usarne una come stima approssimativa. Se invece vorrai ottenere una soluzione più accurata, tutto quello che dovrai fare sarà scegliere una stima per la cifra "dei centesimi" che porti quest'approssimazione tra le prime due. Continuando con questo metodo, potrai ottenere tre cifre decimali per la tua soluzione, e anche quattro, cinque e così via, dipenderà solo da quanto nel dettaglio vorrai arrivare.
- Nel nostro esempio, prendiamo 6,33 come stima con due cifre decimali. Moltiplichiamo 6,33 per se stesso ottenendo 6,33 × 6,33 = 40,0689. Siccome il risultato è leggermente maggiore del nostro numero di partenza, proveremo con un numero leggermente inferiore, come 6,32; 6,32 × 6,32 = 39,9424. Questo risultato è leggermente inferiore al nostro numero di partenza, quindi adesso sappiamo che la radice esatta si situa tra 6,33 e 6,32. Se volessimo continuare nel dettaglio, dovremmo semplicemente continuare a usare lo stesso metodo per ottenere una soluzione via via più precisa.
Pubblicità
Consigli
- Per trovare soluzioni veloci, usa una calcolatrice. La maggior parte delle calcolatrici moderne sono in grado di trovare le radici quadrate immediatamente. Di solito, tutto quello che devi fare è solamente scrivere il numero e premere il tasto con il simbolo della radice quadrata. Per trovare la radice quadrata di 841 per esempio, dovresti solo premere: 8, 4, 1, (√) e ottenere come risposta 39
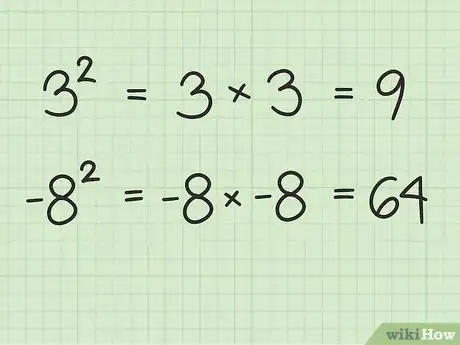
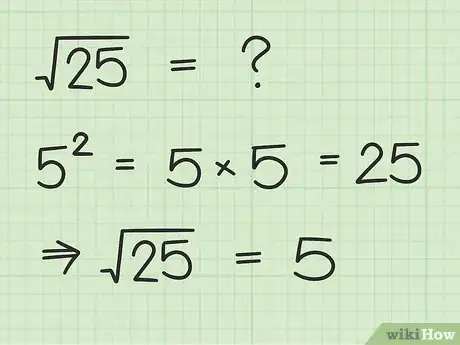


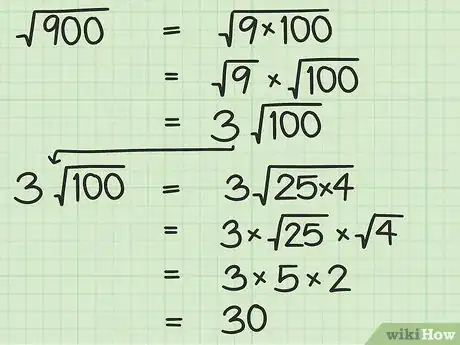
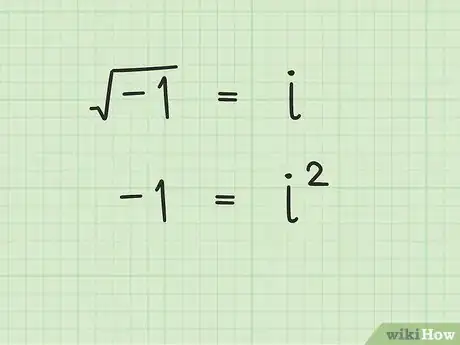

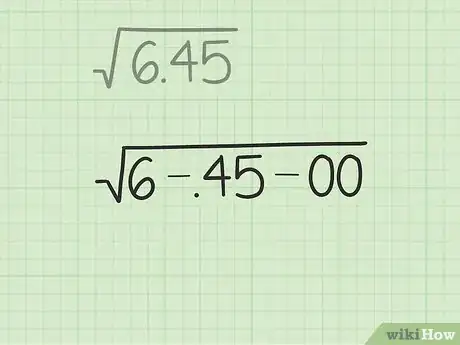
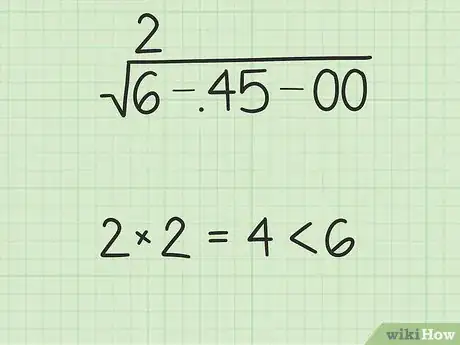
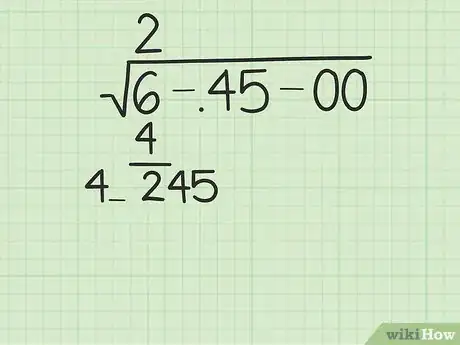
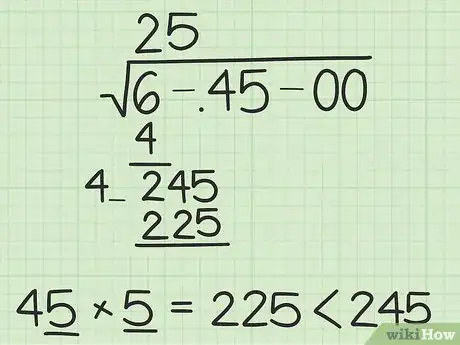
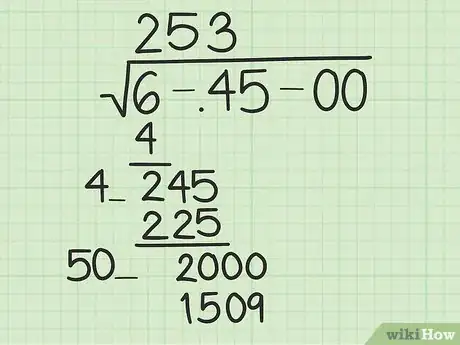
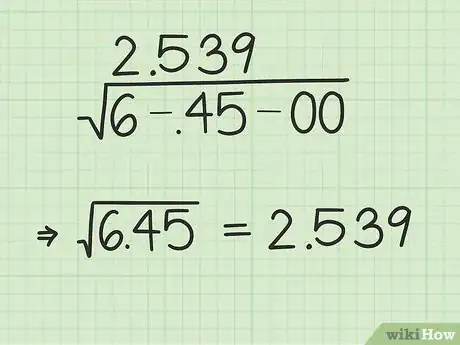
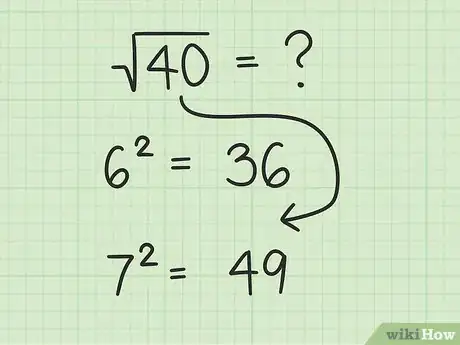
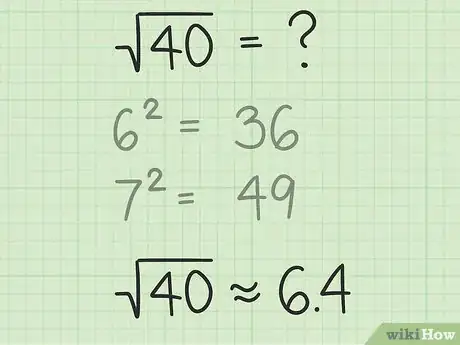





-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
