X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 80 652 volte
Esercitarsi a scomporre i numeri consente agli studenti di comprendere gli schemi generali e le relazioni fra le cifre di numeri elevati e tra i numeri di un'equazione. Puoi scomporre i numeri in centinaia, decine e unità o scomporli in addendi.
Passaggi
Metodo 1
Metodo 1 di 3:
Scomporre in Centinaia, Decine e Unità[1]
-
1Impara la differenza fra "decine" e "unità." In un numero a due cifre senza la virgola (o il punto decimale), le due cifre rappresentano le “decine” e le “unità”. Le “decine” si trovano a sinistra, mentre le “unità” sono sulla destra.
- Il numero che rappresenta le “unità” può essere letto esattamente come appare. Gli unici numeri che costituiscono le “unità” sono i numeri da 0 a 9 (zero, uno, due, tre, quattro, cinque, sei, sette, otto e nove).
- Il numero che rappresenta le “decine” ha lo stesso aspetto del numero che costituisce le unità. Tuttavia, se viene visualizzato separatamente, questo numero in realtà è seguito da uno 0, che lo rende maggiore di un numero nelle “unità”. I numeri appartenenti alle “decine” includono: 10, 20, 30, 40, 50, 60, 70, 80 e 90 (dieci, venti, trenta, quaranta, cinquanta, sessanta, settanta, ottanta e novanta).
-
2Scomponi un numero di due cifre. Quando hai un numero di due cifre, esso è composto dalle “unità” e dalle “decine”. Per scomporre un numero di questo tipo, dovrai dividerlo nelle parti che lo compongono.
-
Esempio: Scomponi il numero 82.
- L'8 rappresenta le “decine”, quindi questa parte del numero può essere separata e riscritta come 80.
- Il 2 rappresenta le “unità”, quindi questa parte del numero può essere separata e riscritta come 2.
- Nella risposta, dovrai scrivere: 82 = 80 + 2
- Nota anche che il numero scritto nel modo usuale è espresso in "forma standard", mentre un numero scomposto è scritto in "forma estesa".
- Nell'esempio precedente, "82" è la forma standard, mentre "80 + 2" è la forma estesa.
-
Esempio: Scomponi il numero 82.
-
3Introduci le "centinaia". Quando un numero è composto da tre cifre senza la virgola (o il punto decimale), è composto da “unità”, “decine” e “centinaia”. Le “centinaia” sono quelle a sinistra del numero. Le “decine” si trovano al centro, mentre le “unità” sono sulla destra.
- Le “unità” e le “decine” funzionano esattamente come nei numeri a due cifre.
- Il numero che indica le “centinaia” ha lo stesso aspetto di quello che indica le “unità” ma, se visualizzato separatamente, in realtà è seguito da due zeri. I numeri che appartengono alle “centinaia” sono: 100, 200, 300, 400, 500, 600, 700, 800, e 900 (cento, duecento, trecento, quattrocento, cinquecento, seicento, settecento, ottocento e novecento).
-
4Scomponi un numero a tre cifre. Quando hai un numero di tre cifre, esso è composto dalle “unità”, dalle “decine” e dalle “centinaia”. Per scomporre un numero di questo tipo, dovrai dividerlo nelle tre parti che lo compongono
-
Esempio: Scomponi il numero 394.
- Il 3 rappresenta le “centinaia”, quindi questa parte del numero può essere separata e riscritta come 300.
- Il 9 rappresenta le “decine”, quindi questa parte del numero può essere separata e riscritta come 90.
- Il 4 rappresenta le “unità”, quindi questa parte del numero può essere separata e riscritta come 4.
- La risposta finale sarà: 394 = 300 + 90 + 4
- Quando scrivi 394, il numero è in forma standard. Quando scrivi 300 + 90 + 4, il numero è in forma estesa.
-
Esempio: Scomponi il numero 394.
-
5Applica questo schema a numeri sempre più elevati. Puoi scomporre i numeri più elevati utilizzando lo stesso principio.
- Una cifra posta in qualsiasi posizione può essere scomposta in una parte separata sostituendo i numeri alla sua destra con degli zeri. Ciò è sempre valido, a prescindere da quante cifre abbia il numero.
- Esempio: 5.394.128 = 5.000.000 + 300.000 + 90.000 + 4.000 + 100 + 20 + 8
-
6Impara come funzionano i decimali. Puoi scomporre i numeri decimali, ma ogni numero che si trova dopo la virgola dev'essere scomposto in una porzione di numero anch'essa scritta come decimale.
- I “decimi” si utilizzano quando c'è una sola cifra dopo la virgola o il punto decimale (o alla loro destra).
- I “centesimi” si utilizzano quando ci sono due cifre dopo la virgola (o il punto decimale).
- I “millesimi” si utilizzano quando ci sono tre cifre dopo la virgola (o il punto decimale).
-
7Scomponi un numero decimale. Quando hai un numero con delle cifre sia alla sinistra che alla destra della virgola, devi scomporlo considerando entrambe le parti.
- Nota che tutti i numeri a sinistra della virgola possono essere scomposti nello stesso modo in cui si procederebbe se la virgola non fosse presente.
-
Esempio: Scomponi il numero 431,58
- Il 4 rappresenta le “centinaia”, quindi questa parte del numero può essere separata e riscritta come 400
- Il 3 rappresenta le “decine”, quindi questa parte del numero può essere separata e riscritta come 30
- L'1 rappresenta le “unità”, quindi questa parte del numero può essere separata e riscritta come 1
- Il 5 rappresenta i “decimi”, quindi questa parte del numero può essere separata e riscritta come 0,5
- L'8 rappresenta i “centesimi”, quindi questa parte del numero può essere separata e riscritta come 0,08
- La risposta finale sarà: 431,58 = 400 + 30 + 1 + 0,5 + 0,08
Pubblicità
-
1Comprendi il concetto. Quando scomponi un numero nei suoi addendi, lo dividi in diversi set di altri numeri (gli addendi, appunto) che possono essere sommati per ottenere il valore originale.
- Quando si sottrae un addendo dal numero originale, si ottiene il secondo addendo.
- Sommando gli addendi, il totale ottenuto sarà il numero originale.
-
2Esercitati con numeri con poche cifre. Questo esercizio è facilissimo quando hai numeri a una sola cifra (numeri che possiedono solo le “unità”).
- Puoi combinare questi principi con quelli appresi nella sezione “Scomporre in Centinaia, Decine e Unità” per scomporre i numeri più elevati, ma poiché ci sono numerosissime composizioni di addendi per i numeri più alti, questo metodo sarà impossibile da utilizzare da solo con tali numeri.
-
3Trova tutte le diverse combinazioni di addendi. Per scomporre un numero in addendi dovrai scrivere tutti i possibili modi in cui puoi ottenere il numero originale sommano numeri minori di esso.
-
Esempio: Scomponi il numero 7 nei sui diversi addendi.
- 7 = 0 + 7
- 7 = 1 + 6
- 7 = 2 + 5
- 7 = 3 + 4
- 7 = 4 + 3
- 7 = 5 + 2
- 7 = 6 + 1
- 7 = 7 + 0
-
Esempio: Scomponi il numero 7 nei sui diversi addendi.
-
4Usa supporti visivi, se necessario. Per chi sta cercando di imparare questo concetto per la prima volta, può essere utile usare dei supporti visivi per dimostrare il processo in modo pratico.
- Inizia con un certo numero di oggetti. Ad esempio, se il numero è sette, inizia con sette caramelle.
- Separale in due gruppi mettendone una da parte. Conta quelle rimaste e spiega che le sette caramelle iniziali sono state scomposte in “uno” e “sei.”
- Continua a separare le caramelle in due gruppi togliendole una per volta dal primo e spostandole nel secondo. Conta le caramelle in entrambi i gruppi ad ogni spostamento.
- Puoi usare una grande varietà di materiali, inclusi dolcetti, quadratini di carta, spillette colorate, blocchi o bottoni.
Pubblicità - Inizia con un certo numero di oggetti. Ad esempio, se il numero è sette, inizia con sette caramelle.
Metodo 3
Metodo 3 di 3:
Scomporre per Risolvere le Equazioni[4]
-
1Vediamo una semplice equazione costituita da un'addizione. Puoi combinare entrambi i metodi di scomposizione per riscrivere questo tipo di equazioni in forme diverse.
- Ciò è più facile se applicato a semplici equazioni composte da addizioni, ma diventa meno pratico se applicato a equazioni più lunghe.
-
2Scomponi i numeri presenti nell'equazione. Osserva l'equazione e scomponi i numeri in "decine" e "unità". Se necessario, puoi scomporre ulteriormente le "unità" in numeri più piccoli.
-
Esempio: Scomponi e risolvi l'equazione: 31 + 84
- Puoi scomporre 31 in: 30 + 1
- Puoi scomporre 84 in: 80 + 4
-
Esempio: Scomponi e risolvi l'equazione: 31 + 84
-
3Riscrivi l'equazione in una forma più semplice. L'equazione può essere riscritta in modo che ogni parte in cui l'hai scomposta sia isolata, oppure puoi combinare alcune delle parti scomposte per renderla più comprensibile.
- Esempio: 31 + 84 = 30 + 1 + 80 + 4 = 30 + 80 + 5 = 100 + 10 + 5
-
4Risolvi l'equazione. Dopo aver riscritto l'equazione in una forma più semplice e comprensibile, tutto ciò che devi fare è sommare i numeri e calcolare il totale.
- Esempio: 100 + 10 + 5 = 115
Pubblicità
Riferimenti
Informazioni su questo wikiHow
Pubblicità

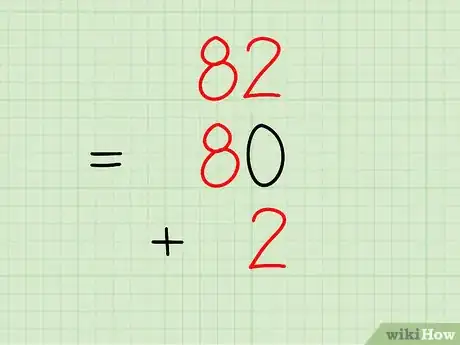

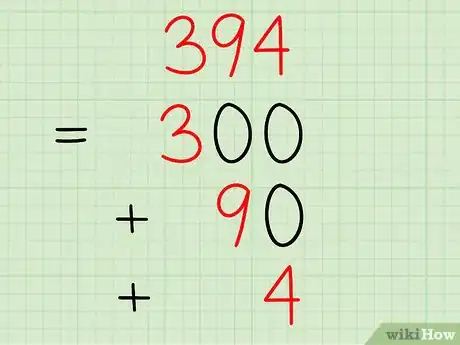



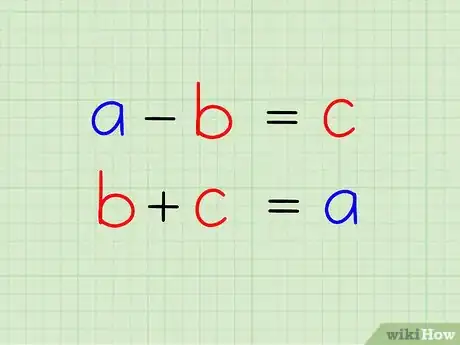
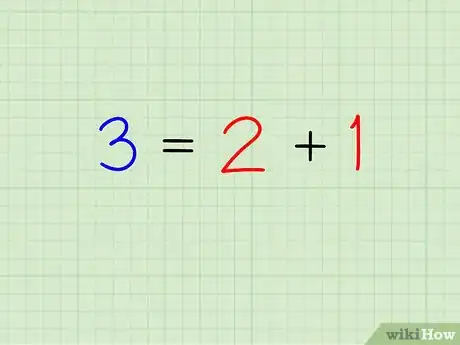


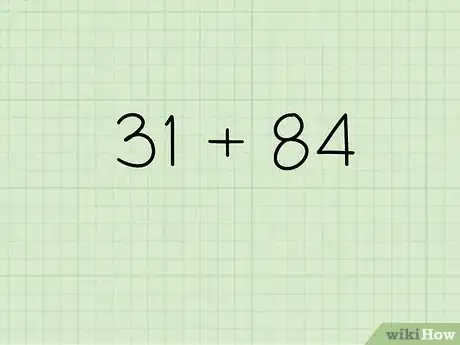

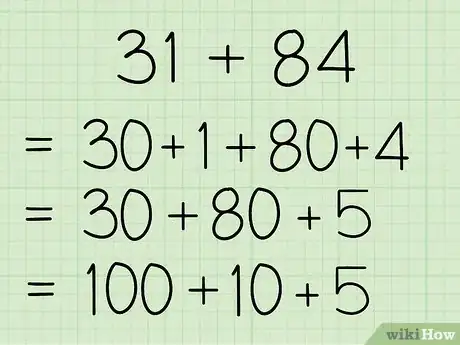





-to-Grams-(g)-Step-12-Version-4.webp)













